Giải bài tập Toán 12 Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số | Cánh Diều
Hướng dẫn giải chi tiết SBT Toán 12 - Cánh diều, Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số.
Giải bài tập Bài 1. Tính đơn điệu của hàm số.

Bài 1 trang 10 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm f'(x) như sau: Hàm số đã cho nghịch biến trên khoảng nào dưới đây? Bài 1 trang 10 SBT Toán 12 Tập 1
Bài 2 trang 10 SBT Toán 12 Tập 1
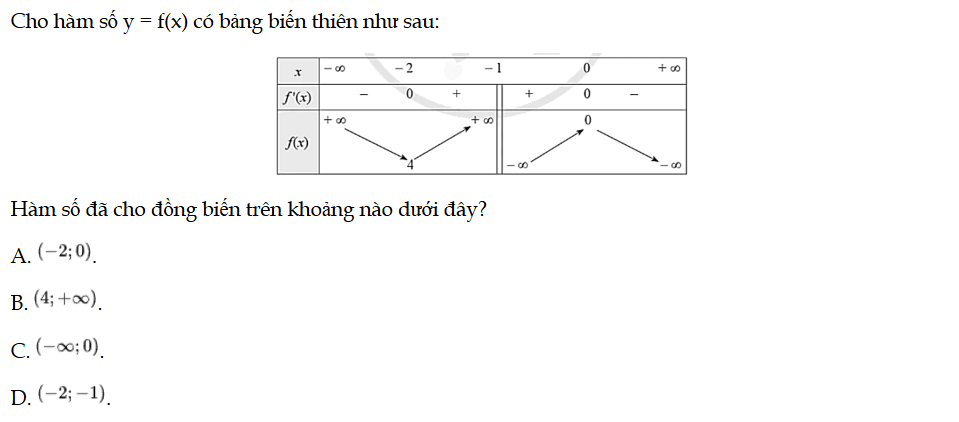
Cho hàm số y = f(x) có bảng biến thiên như sau: Hàm số đã cho đồng biến trên khoảng nào dưới đây? Bài 2 trang 10 SBT Toán 12 Tập 1

Bài 3 trang 10 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm f'(x)= −x(2x – 5), ∀x ∈ ℝ. Khẳng định nào dưới đây đúng? Bài 3 trang 10 SBT Toán 12 Tập 1

Bài 4 trang 11 SBT Toán 12 Tập 1
Cho hàm số y = −x3 + 3x2 − 4. Mệnh đề nào dưới đây là đúng? Bài 4 trang 11 SBT Toán 12 Tập 1

Bài 5 trang 11 SBT Toán 12 Tập 1
Cho hàm số y =f(x), mệnh đề nào dưới đây là đúng? Bài 5 trang 11 SBT Toán 12 Tập 1

Bài 6 trang 11 SBT Toán 12 Tập 1
Trong các hàm số sau, hàm số đồng biến trên ℝ là: Bài 6 trang 11 SBT Toán 12 Tập 1
Bài 7 trang 11 SBT Toán 12 Tập 1
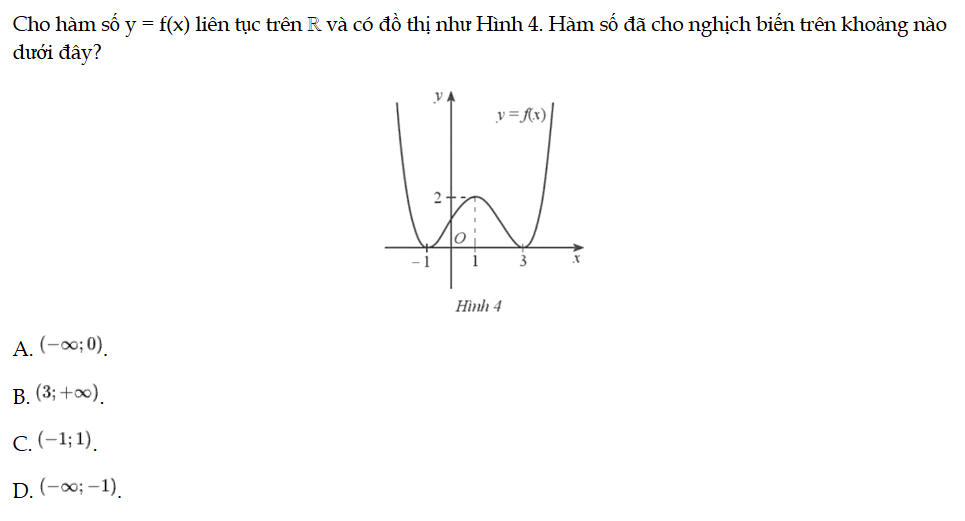
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 4. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? Bài 7 trang 11 SBT Toán 12 Tập 1

Bài 8 trang 11 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm trên ℝ và bảng xét dấu của đạo hàm như sau: Số điểm cực trị của hàm số đã cho là: Bài 8 trang 11 SBT Toán 12 Tập 1

Bài 9 trang 12 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có bảng biến thiên như sau, điểm cực đại của hàm số đã cho là: Bài 9 trang 12 SBT Toán 12 Tập 1
Bài 10 trang 12 SBT Toán 12 Tập 1
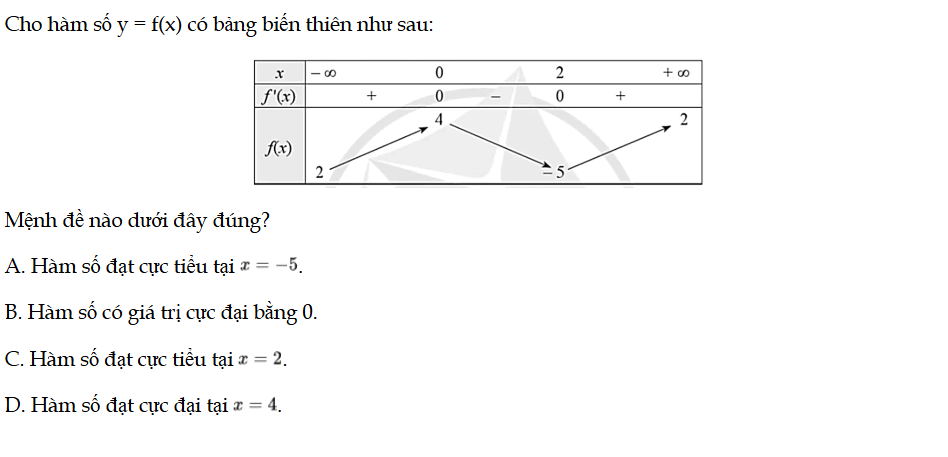
Cho hàm số y = f(x) có bảng biến thiên như sau, mệnh đề nào dưới đây đúng? Bài 10 trang 12 SBT Toán 12 Tập 1
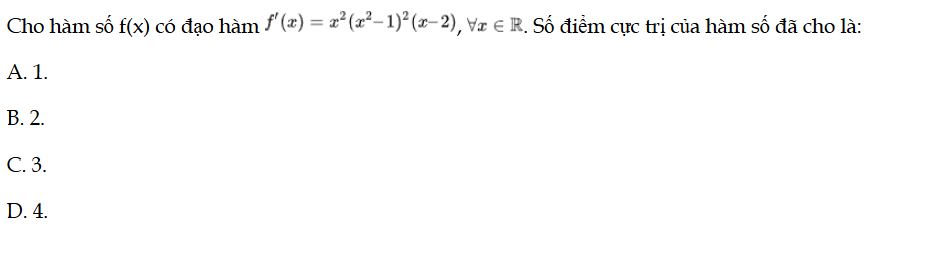
Bài 11 trang 12 SBT Toán 12 Tập 1
Cho hàm số f(x) có đạo hàm f'(x) = x2(x2 – 1)2(x – 2), ∀x ∈ ℝ. Số điểm cực trị của hàm số đã cho là: Bài 11 trang 12 SBT Toán 12 Tập 1

Bài 12 trang 12 SBT Toán 12 Tập 1
Cho hàm số y = 2x3 + 3x + 2. Kết luận nào sau đây đúng? Bài 12 trang 12 SBT Toán 12 Tập 1
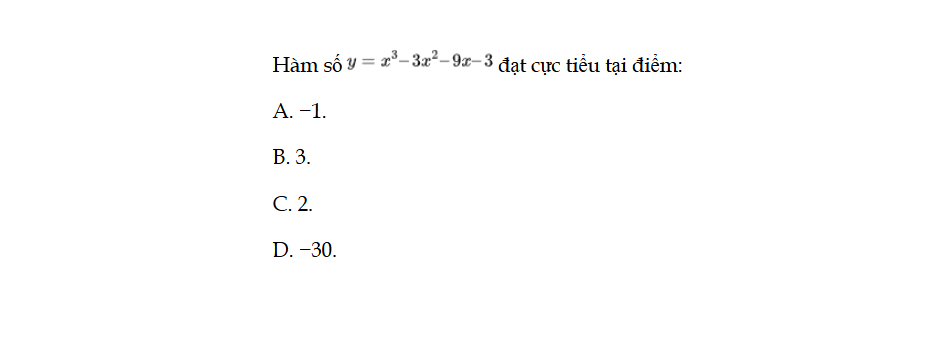
Bài 13 trang 12 SBT Toán 12 Tập 1
Hàm số y = x3 – 3x2 – 9x – 3 đạt cực tiểu tại điểm: Bài 13 trang 12 SBT Toán 12 Tập 1
Bài 14 trang 12 SBT Toán 12 Tập 1
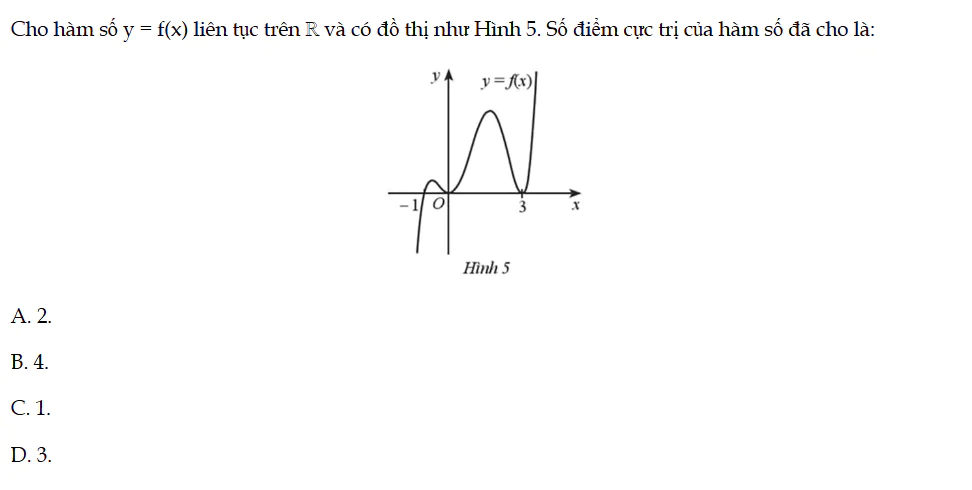
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 5. Số điểm cực trị của hàm số đã cho là. Bài 14 trang 12 SBT Toán 12 Tập 1
Bài 15 trang 13 SBT Toán 12 Tập 1
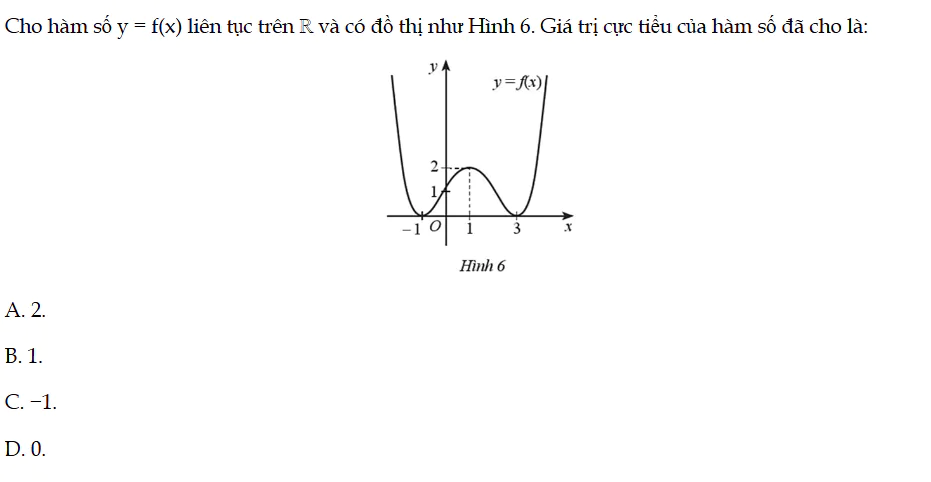
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là: Bài 15 trang 13 SBT Toán 12 Tập 1
Bài 16 trang 13 SBT Toán 12 Tập 1
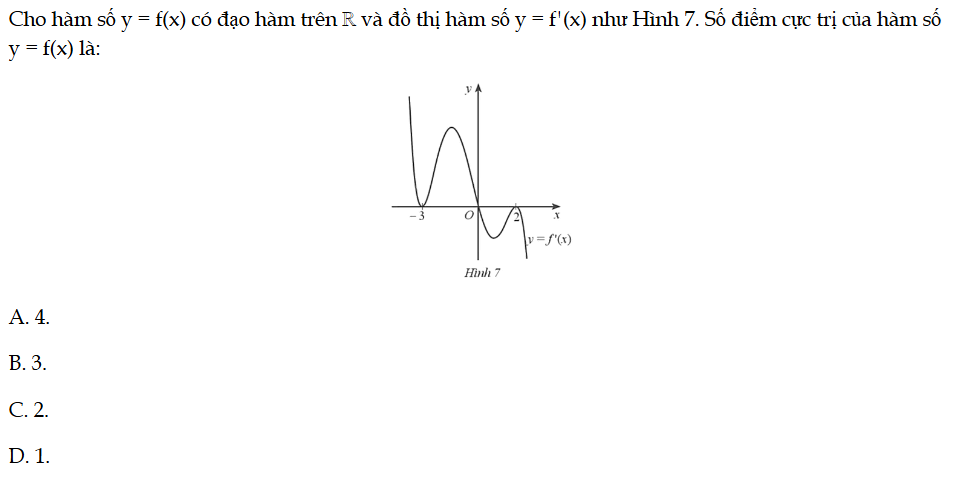
Cho hàm số y = f(x) có đạo hàm trên ℝ và đồ thị hàm số y = f'(x) như Hình 7. Số điểm cực trị của hàm số y = f(x) là: Bài 16 trang 13 SBT Toán 12 Tập 1

Bài 17 trang 13 SBT Toán 12 Tập 1
Cho hàm số y = x3 – 3x + 2. Bài 17 trang 13 SBT Toán 12 Tập 1
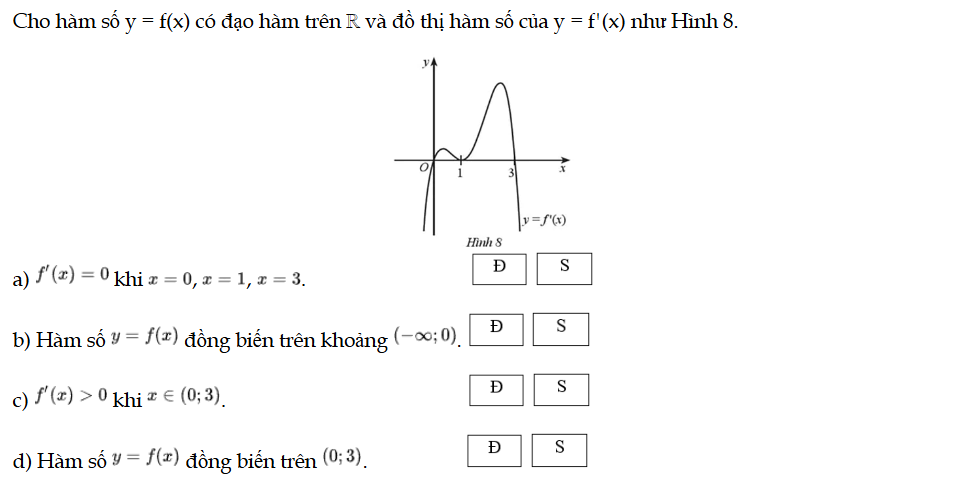
Bài 18 trang 13 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm trên ℝ và đồ thị hàm số của y = f'(x) như Hình 8. Bài 18 trang 13 SBT Toán 12 Tập 1

Bài 19 trang 14 SBT Toán 12 Tập 1
Tìm các khoảng đơn điệu của mỗi hàm số sau: Bài 19 trang 14 SBT Toán 12 Tập 1

Bài 20 trang 14 SBT Toán 12 Tập 1
Tìm điểm cực trị của mỗi hàm số sau. Bài 20 trang 14 SBT Toán 12 Tập 1

Bài 21 trang 14 SBT Toán 12 Tập 1
Dùng đạo hàm của hàm số, hãy giải thích: a) Hàm số y = ax đồng biến trên ℝ khi a > 1, nghịch biến trên ℝ khi 0 < a < 1. Bài 21 trang 14 SBT Toán 12 Tập 1

Bài 22 trang 14 SBT Toán 12 Tập 1
Chứng minh rằng: Bài 22 trang 14 SBT Toán 12 Tập 1

Bài 23 trang 14 SBT Toán 12 Tập 1
Tìm điểm cực trị của mỗi hàm số sau: Bài 23 trang 14 SBT Toán 12 Tập 1

Bài 24 trang 14 SBT Toán 12 Tập 1
Trong một thí nghiệm y học, người ta cấy 1 000 con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: Bài 24 trang 14 SBT Toán 12 Tập 1

Bài 25 trang 15 SBT Toán 12 Tập 1
Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình s(t), trong đó t tính bằng giây và s tính bằng mét. Trong khoảng thời gian nào của 5 giây đầu tiên thì vận tốc tức thời của chất điểm tăng lên? Bài 25 trang 15 SBT Toán 12 Tập 1
Giải bài tập Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
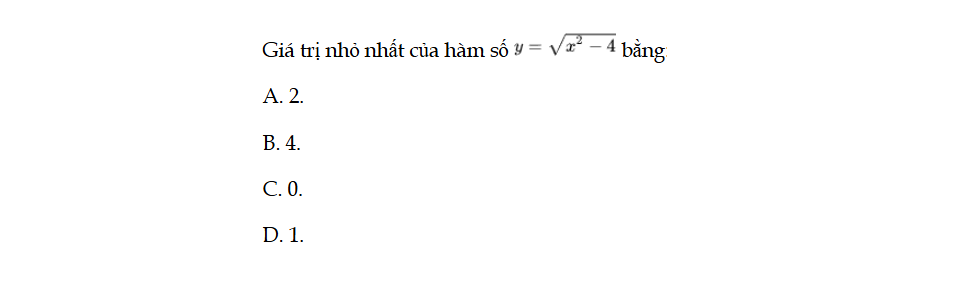
Bài 26 trang 17 SBT Toán 12 Tập 1
Giá trị nhỏ nhất của hàm số y = f(x) bằng. Bài 26 trang 17 SBT Toán 12 Tập 1
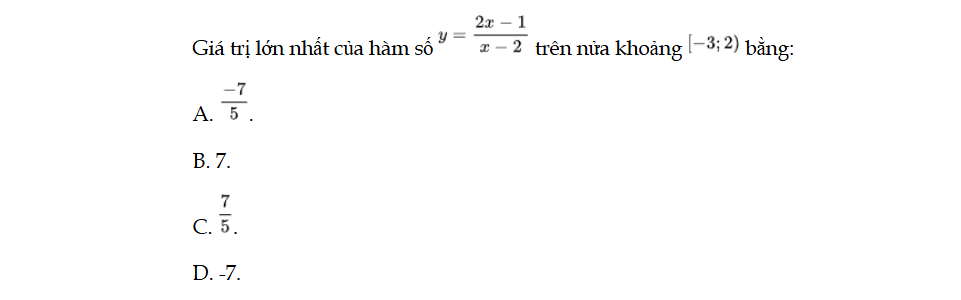
Bài 27 trang 17 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số y trên nửa khoảng [−3; 2) bằng: Bài 27 trang 17 SBT Toán 12 Tập 1
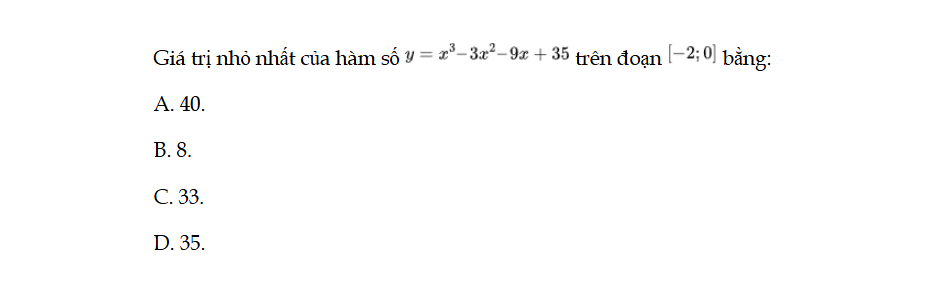
Bài 28 trang 17 SBT Toán 12 Tập 1
Giá trị nhỏ nhất của hàm số y = x3 – 3x2 – 9x + 35 trên đoạn [−2; 0] bằng: Bài 28 trang 17 SBT Toán 12 Tập 1
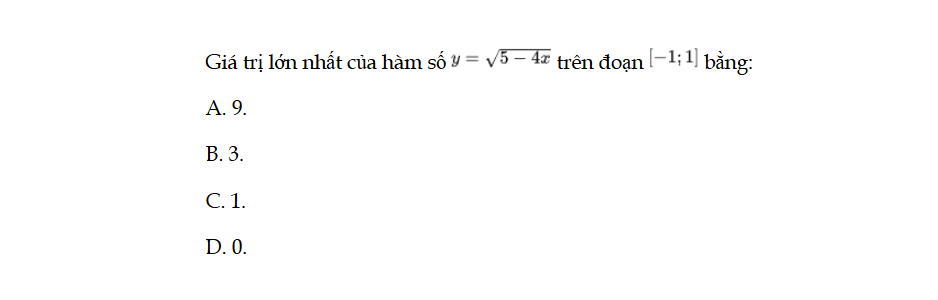
Bài 29 trang 17 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số y = f(x) trên đoạn [−1; 1] bằng. Bài 29 trang 17 SBT Toán 12 Tập 1
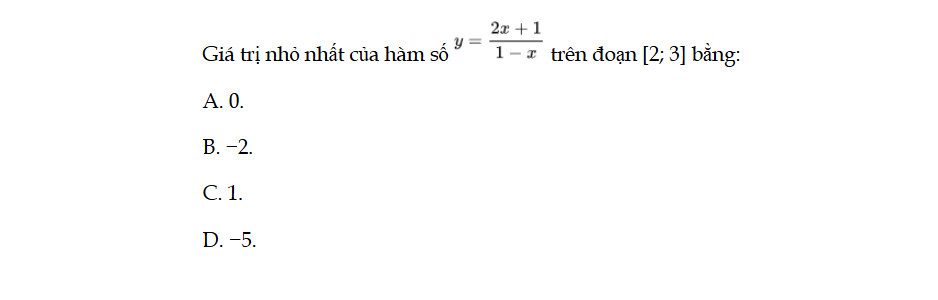
Bài 30 trang 17 SBT Toán 12 Tập 1
Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [2; 3] bằng. Bài 30 trang 17 SBT Toán 12 Tập 1
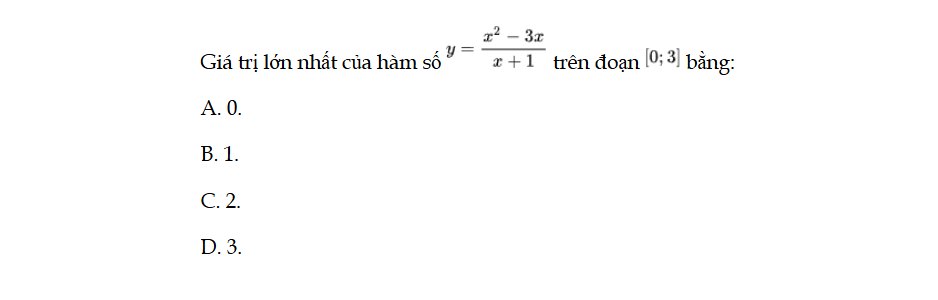
Bài 31 trang 17 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số y =f(x) trên đoạn [0; 3] bằng. Bài 31 trang 17 SBT Toán 12 Tập 1

Bài 32 trang 18 SBT Toán 12 Tập 1
Giá trị nhỏ nhất của hàm số y =f(x) trên đoạn [1; 2] bằng. Bài 32 trang 18 SBT Toán 12 Tập 1

Bài 33 trang 18 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số y = f(x) trên đoạn bằng. Bài 33 trang 18 SBT Toán 12 Tập 1

Bài 34 trang 18 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số y = f(x) trên đoạn [0; 2] bằng. Bài 34 trang 18 SBT Toán 12 Tập 1
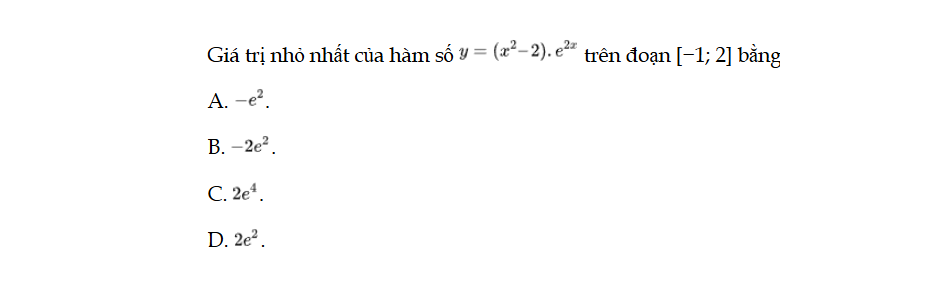
Bài 35 trang 18 SBT Toán 12 Tập 1
Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [−1; 2] bằng. Bài 35 trang 18 SBT Toán 12 Tập 1

Bài 36 trang 18 SBT Toán 12 Tập
Giá trị lớn nhất của hàm số y = f(x) trên đoạn [1; 3] bằng. Bài 36 trang 18 SBT Toán 12 Tập

Bài 37 trang 18 SBT Toán 12 Tập 1
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f(x) lần lượt bằng. Bài 37 trang 18 SBT Toán 12 Tập 1
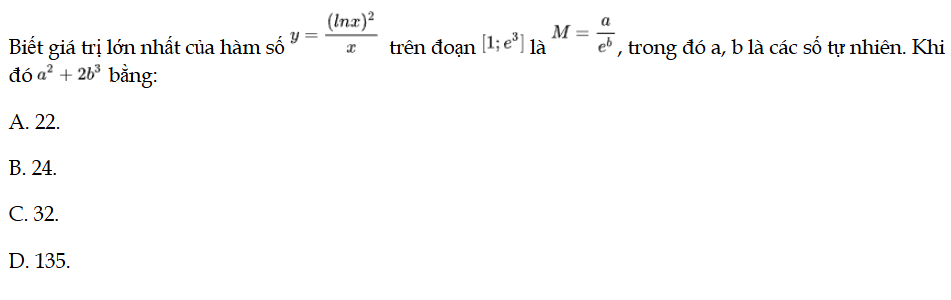
Bài 38 trang 18 SBT Toán 12 Tập 1
Biết giá trị lớn nhất của hàm số y = f(x) trên đoạn [1; e3] là M, trong đó a, b là các số tự nhiên. Khi đó a2+ 2b3 bằng. Bài 38 trang 18 SBT Toán 12 Tập 1

Bài 39 trang 18 SBT Toán 12 Tập 1
Cho hàm số y = x2. lnx. Các ý sau đây là đúng hay sai? Giải thích vì sao? Bài 39 trang 18 SBT Toán 12 Tập 1

Bài 40 trang 19 SBT Toán 12 Tập 1
Bác Lâm muốn gò một cái thùng bằng tôn dạng hình hộp chữ nhật không nắp có đáy là hình vuông và đựng đầy được 32 lít nước. Gọi độ dài cạnh đáy của thùng là x (dm), chiều cao của thùng là h (dm). Bài 40 trang 19 SBT Toán 12 Tập 1

Bài 41 trang 19 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của mỗi hàm số sau: Bài 41 trang 19 SBT Toán 12 Tập 1

Bài 42 trang 19 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau: Bài 42 trang 19 SBT Toán 12 Tập 1

Bài 43 trang 20 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau: Bài 43 trang 20 SBT Toán 12 Tập 1

Bài 44 trang 20 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau. Bài 44 trang 20 SBT Toán 12 Tập 1
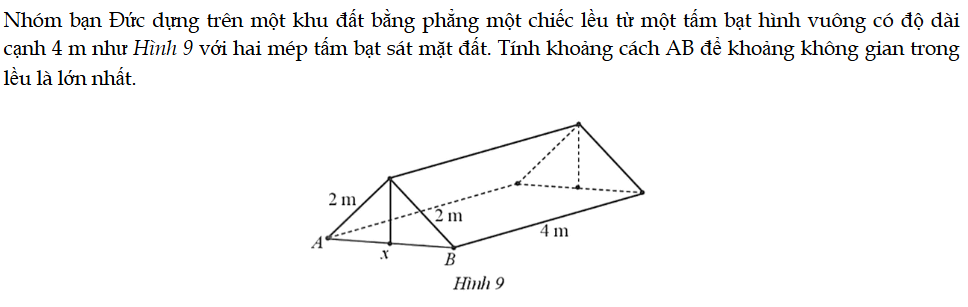
Bài 45 trang 20 SBT Toán 12 Tập 1
Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông có độ dài cạnh 4 m như Hình 9 với hai mép tấm bạt sát mặt đất. Tính khoảng cách AB để khoảng không gian trong lều là lớn nhất. Bài 45 trang 20 SBT Toán 12 Tập 1

Bài 46 trang 20 SBT Toán 12 Tập 1
Nồng độ C của một loại hóa chất trong máu sau t giờ vào cơ thể được cho bởi công thức: C(t). Sau khoảng bao nhiêu giờ tiêm thì nồng độ của hóa chất trong máu là cao nhất? Bài 46 trang 20 SBT Toán 12 Tập 1

Bài 47 trang 20 SBT Toán 12 Tập 1
Khối lượng riêng S (kg/dm3) của nước phụ thuộc vào nhiệt độ T (°C) được cho bởi công thức: a) Tính khối lượng riêng của nước ở nhiệt độ 25 °C. b) Ở nhiệt độ nào thì khối lượng riêng của nước là lớn nhất? Bài 47 trang 20 SBT Toán 12 Tập 1
Giải bài tập Bài 3. Đường tiệm cận của đồ thị hàm số.
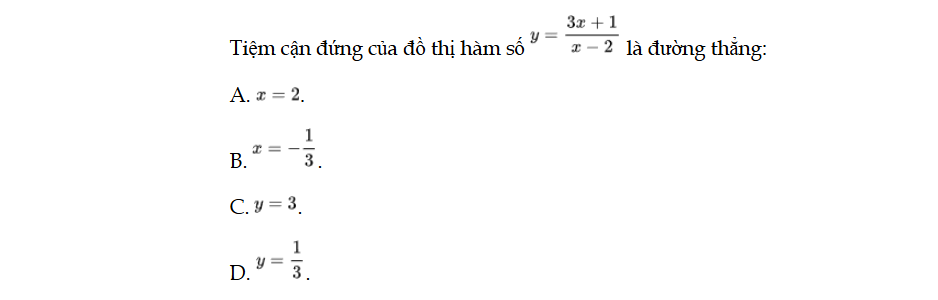
Bài 48 trang 23 SBT Toán 12 Tập 1
Tiệm cận đứng của đồ thị hàm số y = f(x) là đường thẳng. Bài 48 trang 23 SBT Toán 12 Tập 1
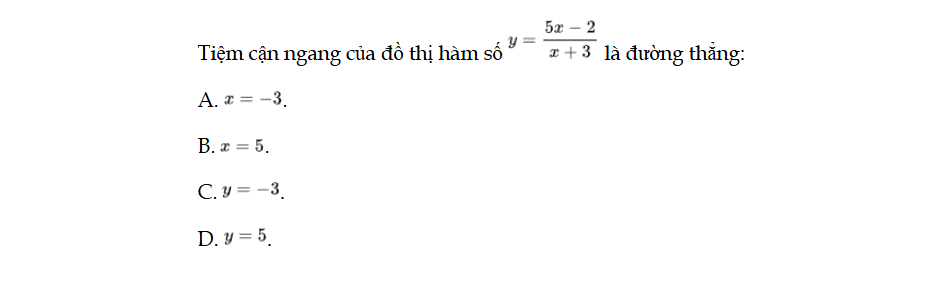
Bài 49 trang 23 SBT Toán 12 Tập 1
Tiệm cận ngang của đồ thị hàm số y = f(x) là đường thẳng. Bài 49 trang 23 SBT Toán 12 Tập 1

Bài 50 trang 23 SBT Toán 12 Tập 1
Tiệm cận đứng, tiệm cận ngang của đồ thị hàm số y = f(x). Bài 50 trang 23 SBT Toán 12 Tập 1

Bài 51 trang 23 SBT Toán 12 Tập 1
Đồ thị hàm số nào sau đây nhận đường thẳng x = −1 làm tiệm cận đứng? Bài 51 trang 23 SBT Toán 12 Tập 1

Bài 52 trang 23 SBT Toán 12 Tập 1
Tiệm cận xiên của đồ thị hàm số y = f(x) là đường thẳng. Bài 52 trang 23 SBT Toán 12 Tập 1
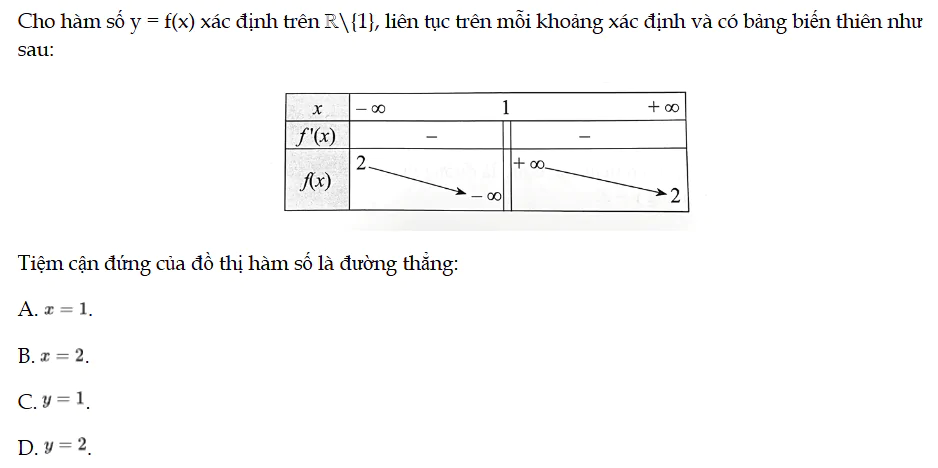
Bài 53 trang 23 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Tiệm cận đứng của đồ thị hàm số là đường thẳng. Bài 53 trang 23 SBT Toán 12 Tập 1

Bài 54 trang 24 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{−2}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Khẳng định nào sau đây là đúng? Bài 54 trang 24 SBT Toán 12 Tập 1

Bài 55 trang 24 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{−2}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Khẳng định nào sau đây là đúng? Bài 55 trang 24 SBT Toán 12 Tập 1
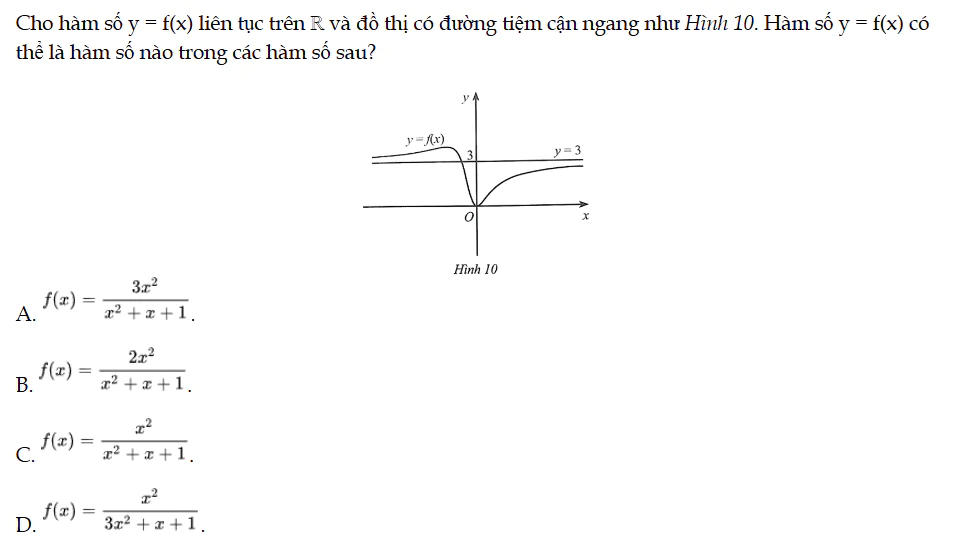
Bài 56 trang 25 SBT Toán 12 Tập 1
Cho hàm số y = f(x) liên tục trên ℝ và đồ thị có đường tiệm cận ngang như Hình 10. Hàm số y = f(x) có thể là hàm số nào trong các hàm số sau? Bài 56 trang 25 SBT Toán 12 Tập 1
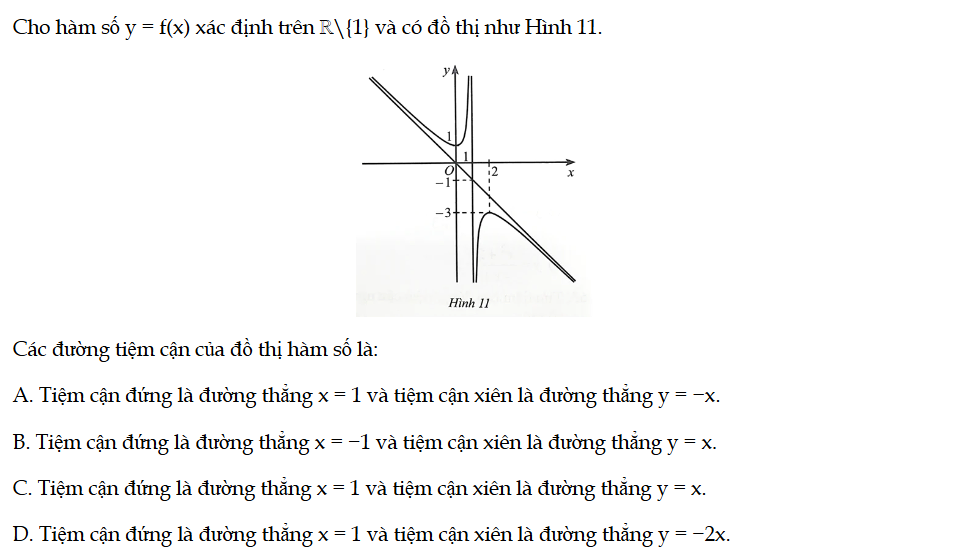
Bài 57 trang 25 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{1} và có đồ thị như Hình 11. Các đường tiệm cận của đồ thị hàm số là. Bài 57 trang 25 SBT Toán 12 Tập 1

Bài 58 trang 25 SBT Toán 12 Tập 1
Giao điểm I của hai đường tiệm cận của đồ thị hàm số y = f(x) là. Bài 58 trang 25 SBT Toán 12 Tập 1

Bài 59 trang 25 SBT Toán 12 Tập 1
Số đường tiệm cận của đồ thị hàm số y = f(x) là. Bài 59 trang 25 SBT Toán 12 Tập 1

Bài 60 trang 25 SBT Toán 12 Tập 1
Số đường tiệm cận của đồ thị hàm số y = f(x) là. Bài 60 trang 25 SBT Toán 12 Tập 1

Bài 61 trang 26 SBT Toán 12 Tập 1
Số đường tiệm cận của đồ thị hàm số y = f(x) là. Bài 61 trang 26 SBT Toán 12 Tập 1

Bài 62 trang 26 SBT Toán 12 Tập 1
Cho hàm số y = f(x), các phát biểu sau đây đúng hay sai? Giải thích vì sao? Bài 62 trang 26 SBT Toán 12 Tập 1

Bài 63 trang 26 SBT Toán 12 Tập 1
Tìm tiệm cận đứng, tiệm cận ngang của đồ thị mỗi hàm số sau. Bài 63 trang 26 SBT Toán 12 Tập 1

Bài 64 trang 26 SBT Toán 12 Tập 1
Tìm tiệm cận đứng, tiệm cận xiên của đồ thị mỗi hàm số sau. Bài 64 trang 26 SBT Toán 12 Tập 1

Bài 65 trang 26 SBT Toán 12 Tập 1
Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau. Bài 65 trang 26 SBT Toán 12 Tập 1

Bài 66 trang 26 SBT Toán 12 Tập 1
Tốc độ đánh máy trung bình S (tính bằng từ trên phút) của một học viên sau t tuần học được cho bởi công thức. Bài 66 trang 26 SBT Toán 12 Tập 1

Bài 67 trang 27 SBT Toán 12 Tập 1
Tổng chi phí để sản xuất x sản phẩm của một xí nghiệp được tính theo công thức T = 20x + 100 000 (nghìn đồng). a) Viết công thức tính chi phí trung bình C(x) của một sản phẩm khi sản xuất được x sản phẩm. Bài 67 trang 27 SBT Toán 12 Tập 1
Giải bài tập Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
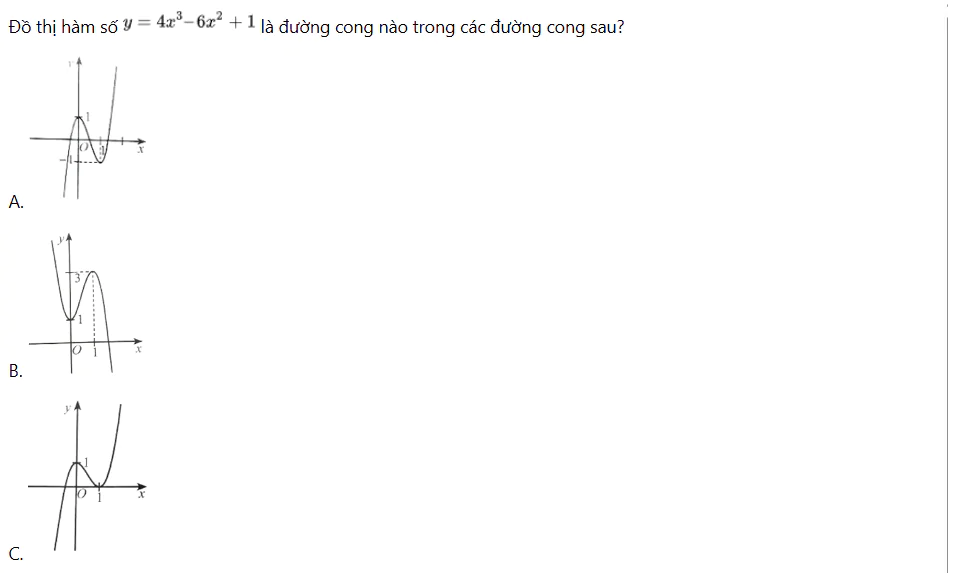
Bài 68 trang 34 SBT Toán 12 Tập 1
Đồ thị hàm số y = 4x3 – 6x2 + 1 là đường cong nào trong các đường cong sau? Bài 68 trang 34 SBT Toán 12 Tập 1

Bài 69 trang 34 SBT Toán 12 Tập 1
Đồ thị hàm số y = −x3 – x + 2 là đường cong nào trong các đường cong sau? Bài 69 trang 34 SBT Toán 12 Tập 1

Bài 70 trang 35 SBT Toán 12 Tập 1
Đồ thị hàm số y = f(x) là đường cong nào trong các đường cong sau?

Bài 71 trang 35 SBT Toán 12 Tập 1
Đồ thị hàm số y = f(x) là đường cong nào trong các đường cong sau? Bài 71 trang 35 SBT Toán 12 Tập 1
Bài 72 trang 36 SBT Toán 12 Tập 1
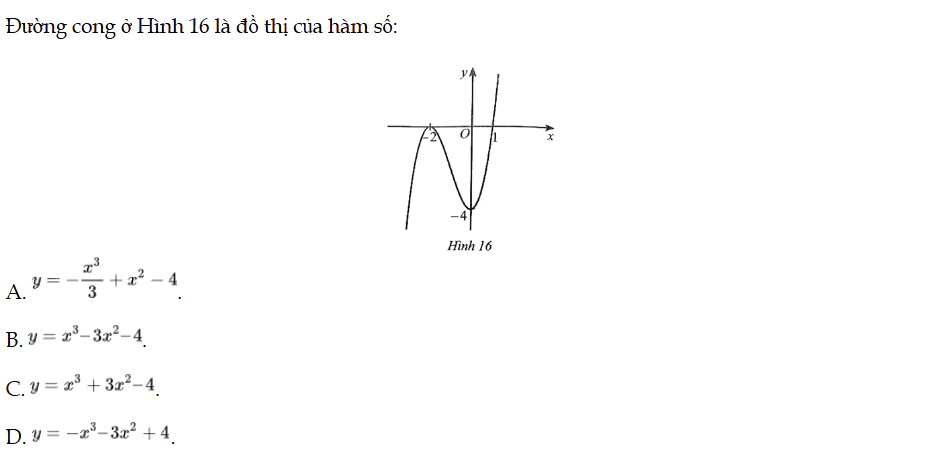
Đường cong ở Hình 16 là đồ thị của hàm số. Bài 72 trang 36 SBT Toán 12 Tập 1
Bài 73 trang 36 SBT Toán 12 Tập 1
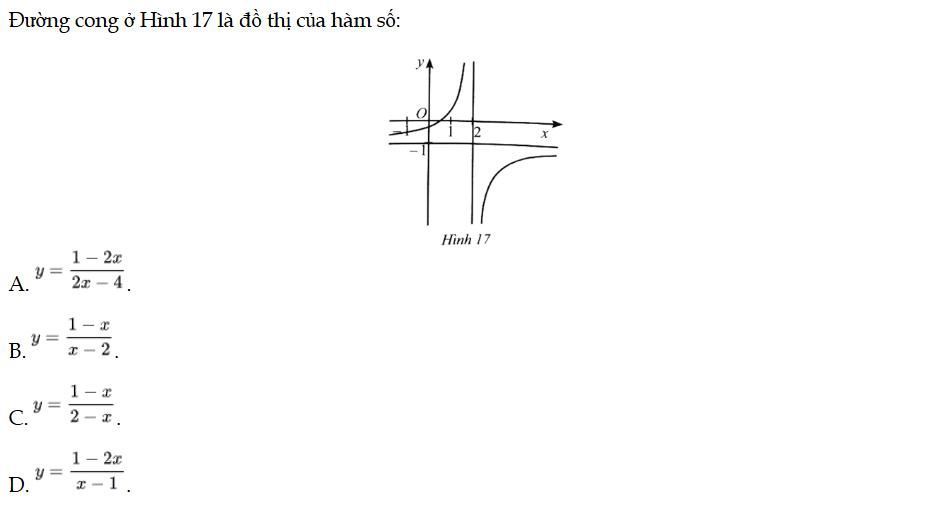
Đường cong ở Hình 17 là đồ thị của hàm số. Bài 73 trang 36 SBT Toán 12 Tập 1
Bài 74 trang 36 SBT Toán 12 Tập 1
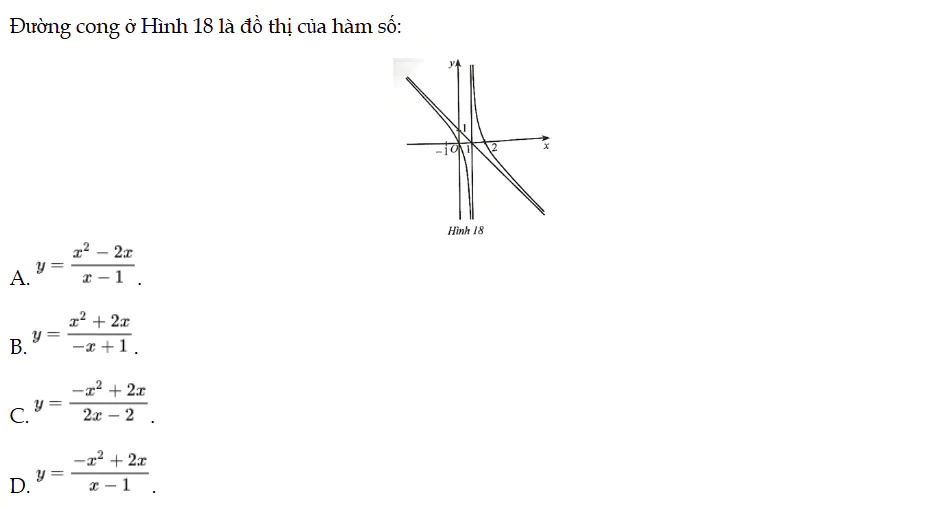
Đường cong ở Hình 18 là đồ thị của hàm số. Bài 74 trang 36 SBT Toán 12 Tập 1
Bài 75 trang 36 SBT Toán 12 Tập 1
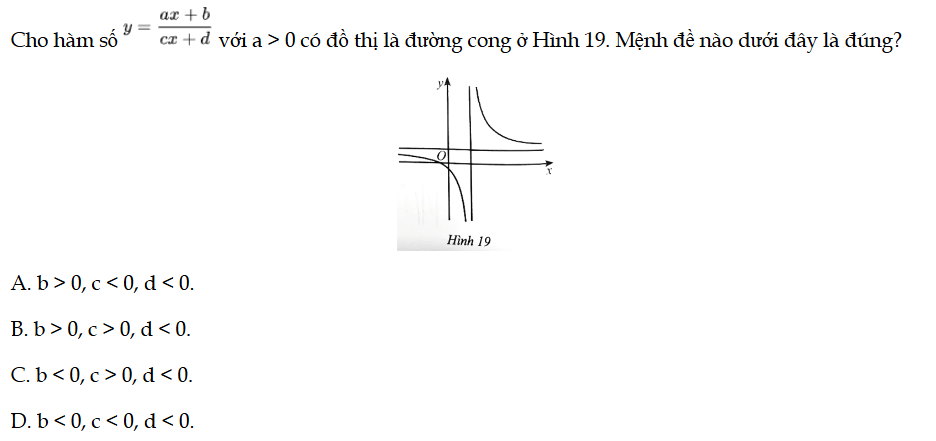
Cho hàm số y = f(x) với a > 0 có đồ thị là đường cong ở Hình 19. Mệnh đề nào dưới đây là đúng? Bài 75 trang 36 SBT Toán 12 Tập 1
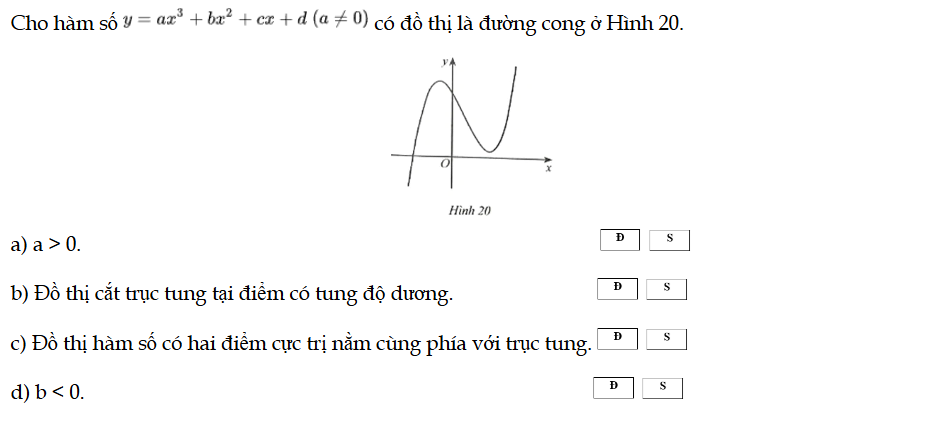
Bài 76 trang 37 SBT Toán 12 Tập 1
Cho hàm số y = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị là đường cong ở Hình 20. Bài 76 trang 37 SBT Toán 12 Tập 1
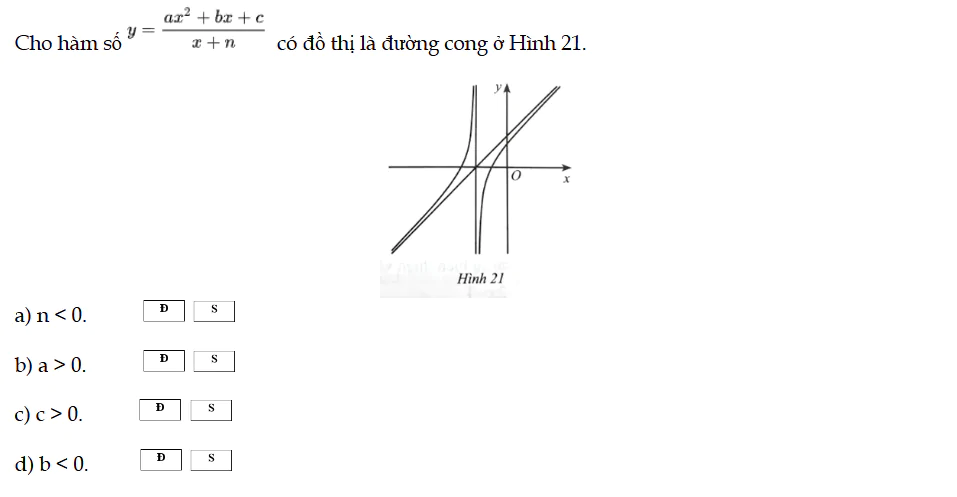
Bài 77 trang 37 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đồ thị là đường cong ở Hình 21. Bài 77 trang 37 SBT Toán 12 Tập 1

Bài 78 trang 37 SBT Toán 12 Tập 1
Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22. Bài 78 trang 37 SBT Toán 12 Tập 1

Bài 79 trang 38 SBT Toán 12 Tập 1
Cho hàm số y = f(x) với (a, m ≠ 0) có đồ thị là đường cong như Hình 23. Bài 79 trang 38 SBT Toán 12 Tập 1

Bài 80 trang 38 SBT Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau. Bài 80 trang 38 SBT Toán 12 Tập 1

Bài 81 trang 38 SBT Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau. Bài 81 trang 38 SBT Toán 12 Tập 1

Bài 82* trang 38 SBT Toán 12 Tập 1
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó gắn với hệ trục tọa độ Oxy với mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có tọa độ (−4; 1). Bài 82* trang 38 SBT Toán 12 Tập 1
Giải bài tập Bài tập cuối chương 1

Bài 83 trang 39 SBT Toán 12 Tập 1
Cho hàm số f(x) xác định trên ℝ có bảng xét dấu đạo hàm f'(x) như sau. Khẳng định nào dưới đây là đúng? Bài 83 trang 39 SBT Toán 12 Tập 1

Bài 84 trang 39 SBT Toán 12 Tập 1
Kết luận nào sau đây là đúng đối với hàm số y = f(x)? Bài 84 trang 39 SBT Toán 12 Tập 1

Bài 85 trang 39 SBT Toán 12 Tập 1
Trong các hàm số sau, hàm số nghịch biến trên ℝ là. Bài 85 trang 39 SBT Toán 12 Tập 1
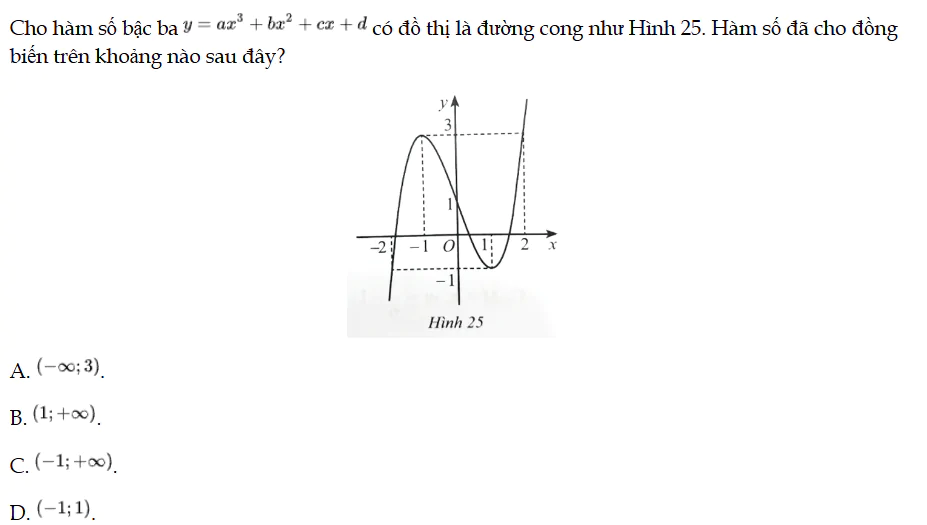
Bài 86 trang 39 SBT Toán 12 Tập 1
Cho hàm số bậc ba y = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 25. Hàm số đã cho đồng biến trên khoảng nào sau đây? Bài 86 trang 39 SBT Toán 12 Tập 1
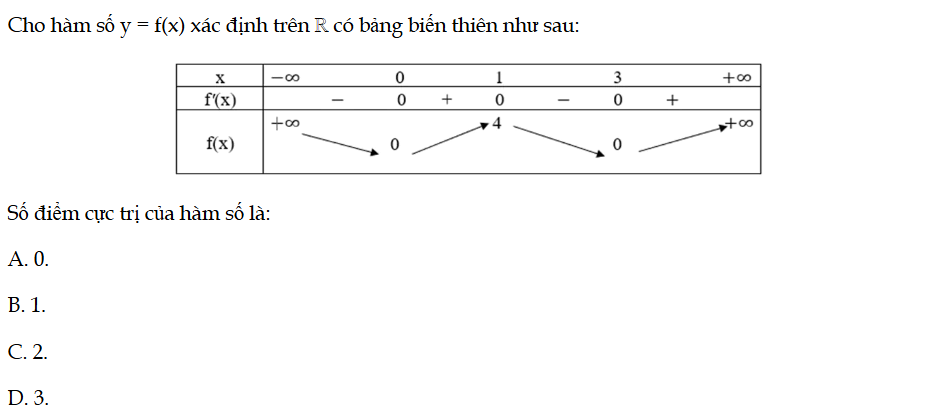
Bài 87 trang 40 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ có bảng biến thiên như sau. Số điểm cực trị của hàm số là. Bài 87 trang 40 SBT Toán 12 Tập 1
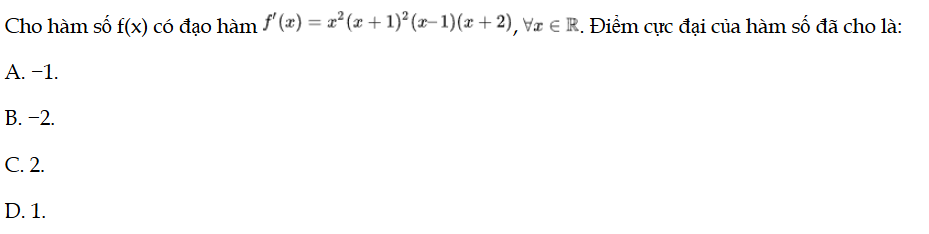
Bài 88 trang 40 SBT Toán 12 Tập 1
Cho hàm số f(x) có đạo hàm f'(x) = x2(x + 1)2(x – 1)(x + 2), ∀x ∈ ℝ. Điểm cực đại của hàm số đã cho là. Bài 88 trang 40 SBT Toán 12 Tập 1
Bài 89 trang 40 SBT Toán 12 Tập 1
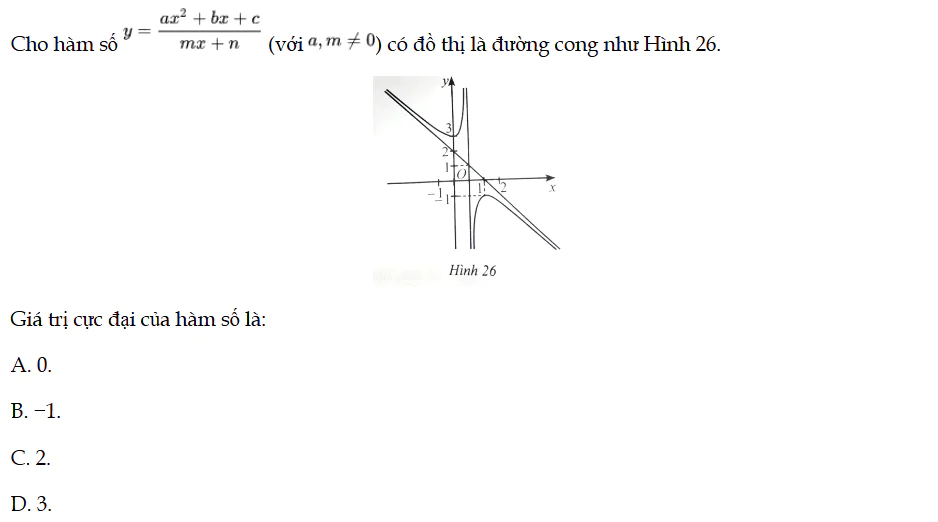
Cho hàm số y = f(x) (với a, m ≠ 0) có đồ thị là đường cong như Hình 26.Giá trị cực đại của hàm số là. Bài 89 trang 40 SBT Toán 12 Tập 1

Bài 90 trang 40 SBT Toán 12 Tập 1
Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [2; 3] bằng. Bài 90 trang 40 SBT Toán 12 Tập 1
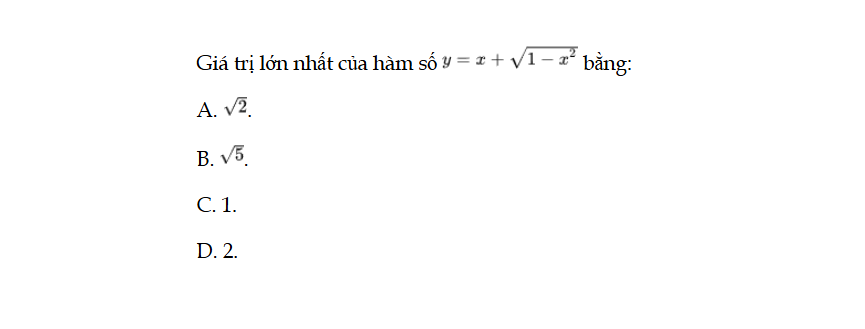
Bài 91 trang 40 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số y = f(x) bằng. Bài 91 trang 40 SBT Toán 12 Tập 1

Bài 92 trang 40 SBT Toán 12 Tập 1
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = x – 2sinx trên đoạn [0; π] lần lượt là. Bài 92 trang 40 SBT Toán 12 Tập 1

Bài 93 trang 41 SBT Toán 12 Tập 1
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = x.lnx trên đoạn [1; e2] bằng. Bài 93 trang 41 SBT Toán 12 Tập 1

Bài 94 trang 41 SBT Toán 12 Tập 1
Đồ thị hàm số nào sau đây nhận đường thẳng y = −2 làm tiệm cận ngang? Bài 94 trang 41 SBT Toán 12 Tập 1
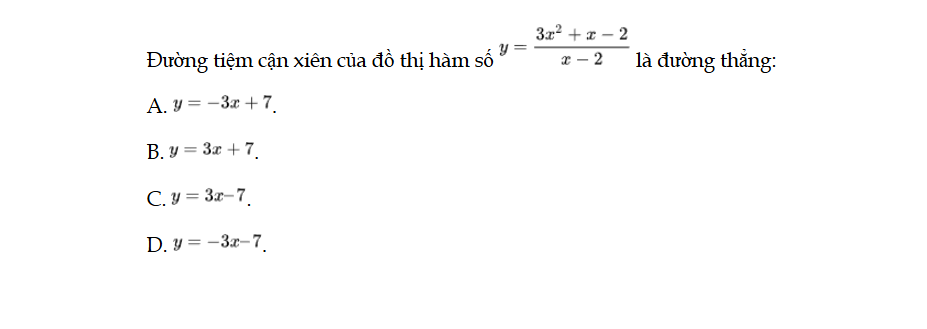
Bài 95 trang 41 SBT Toán 12 Tập 1
Đường tiệm cận xiên của đồ thị hàm số y = f(x) là đường thẳng. Bài 95 trang 41 SBT Toán 12 Tập 1
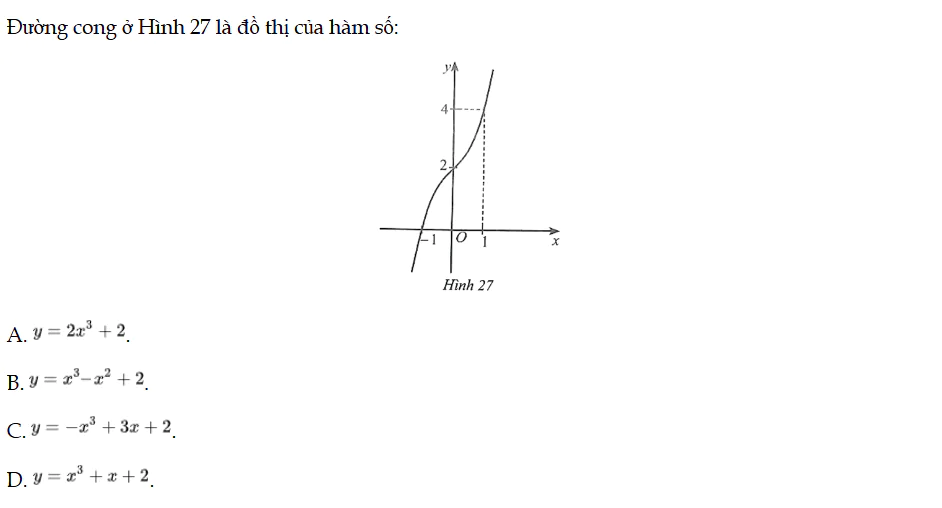
Bài 96 trang 41 SBT Toán 12 Tập 1
Đường cong ở Hình 27 là đồ thị của hàm số. Bài 96 trang 41 SBT Toán 12 Tập 1
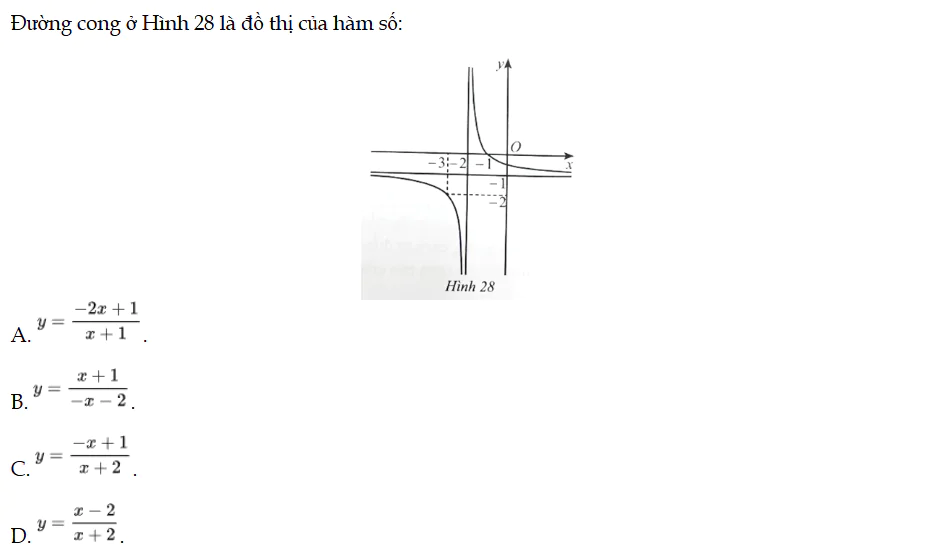
Bài 97 trang 41 SBT Toán 12 Tập 1
Đường cong ở Hình 28 là đồ thị của hàm số. Bài 97 trang 41 SBT Toán 12 Tập 1
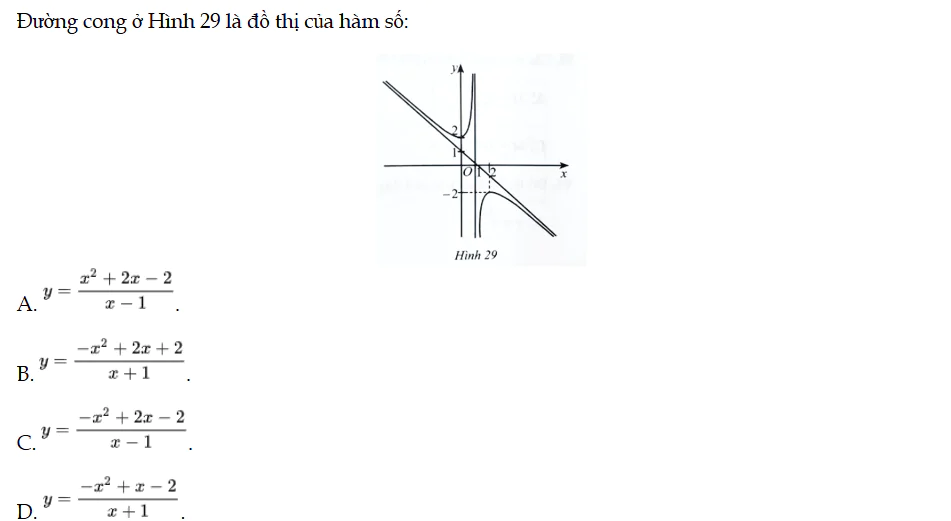
Bài 98 trang 42 SBT Toán 12 Tập 1
Đường cong ở Hình 29 là đồ thị của hàm số. Bài 98 trang 42 SBT Toán 12 Tập 1

Bài 99 trang 42 SBT Toán 12 Tập 1
Cho hàm số y = x.ex. Bài 99 trang 42 SBT Toán 12 Tập 1

Bài 99 trang 42 SBT Toán 12 Tập 1
Cho hàm số y = x.ex. Bài 99 trang 42 SBT Toán 12 Tập 1

Bài 100 trang 42 SBT Toán 12 Tập 1
Cho hàm số y = f(x). Bài 100 trang 42 SBT Toán 12 Tập 1

Bài 101 trang 42 SBT Toán 12 Tập 1
Cho hàm số y = f(x). Bài 101 trang 42 SBT Toán 12 Tập 1
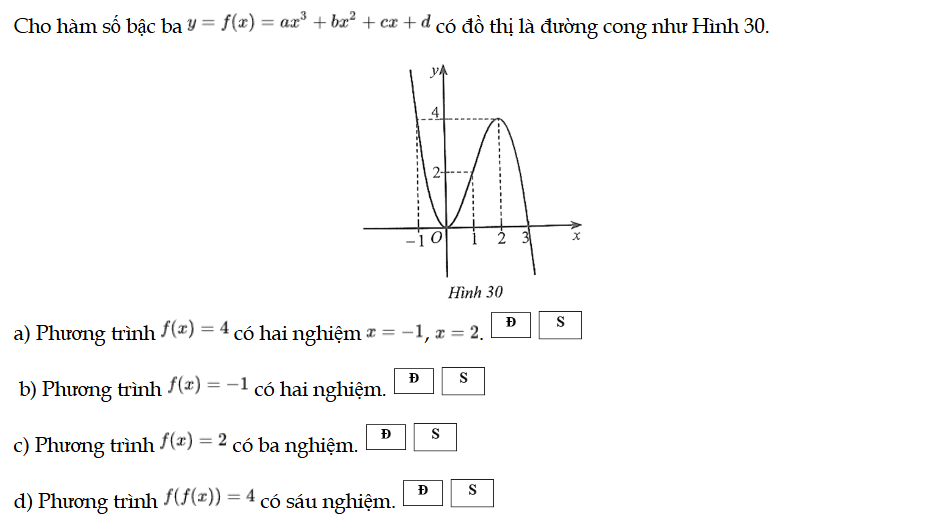
Bài 102 trang 43 SBT Toán 12 Tập 1
Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 30. Bài 102 trang 43 SBT Toán 12 Tập 1
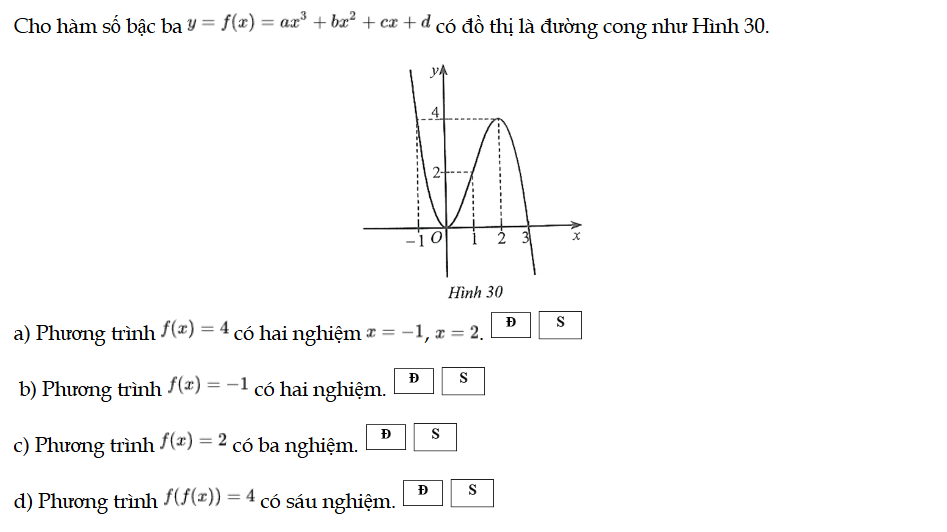
Bài 103 trang 43 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên các khoảng (−∞; −1) và (1; +∞), đồ thị hàm số là đường cong và có bốn đường tiệm cận như Hình 31. Bài 103 trang 43 SBT Toán 12 Tập 1

Bài 104 trang 43 SBT Toán 12 Tập
Cho hàm số y = f(x) xác định trên ℝ\{−2} và có bảng biến thiên như sau. Bài 104 trang 43 SBT Toán 12 Tập

Bài 105 trang 43 SBT Toán 12 Tập 1
Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị mỗi hàm số sau. Bài 105 trang 43 SBT Toán 12 Tập 1

Bài 106 trang 44 SBT Toán 12 Tập 1
Tìm tiệm cận đứng, tiệm cận ngang và tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau. Bài 106 trang 44 SBT Toán 12 Tập 1

Bài 107 trang 44 SBT Toán 12 Tập 1
Tìm giá trị nhỏ nhất và giá trị lớn nhất của mỗi hàm số. Bài 107 trang 44 SBT Toán 12 Tập 1

Bài 108 trang 44 SBT Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau. Bài 108 trang 44 SBT Toán 12 Tập 1
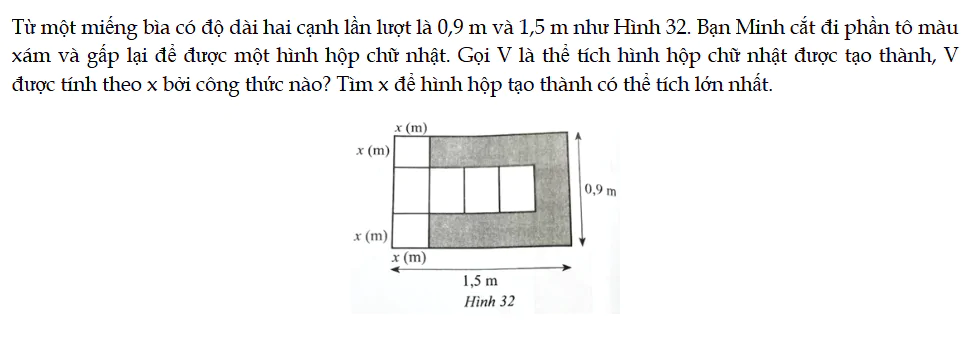
Bài 109 trang 44 SBT Toán 12 Tập 1
Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32. Bạn Minh cắt đi phần tô màu xám và gấp lại để được một hình hộp chữ nhật. Gọi V là thể tích hình hộp chữ nhật được tạo thành, V được tính theo x bởi công thức nào?

Bài 110* trang 44 SBT Toán 12 Tập 1
Một nhà in sử dụng các trang giấy hình chữ nhật để in sách. Sau khi để lề trái, lề phải, lề trên và lề dưới theo số liệu được cho ở Hình 33 thì diện tích phần in chữ trên trang sách là 24 inch2. Bài 110* trang 44 SBT Toán 12 Tập 1
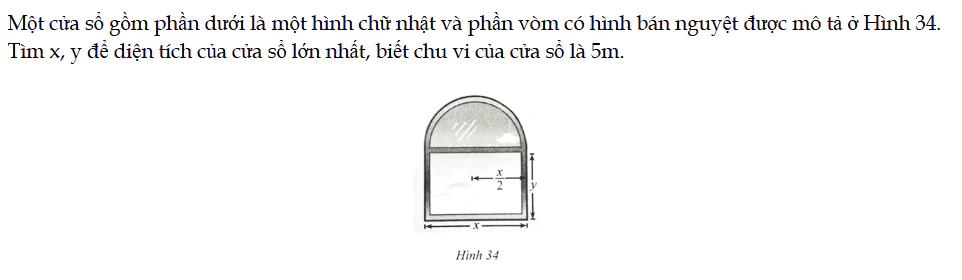
Bài 111* trang 45 SBT Toán 12 Tập 1
Một cửa sổ gồm phần dưới là một hình chữ nhật và phần vòm có hình bán nguyệt được mô tả ở Hình 34. Tìm x, y để diện tích của cửa sổ lớn nhất, biết chu vi của cửa sổ là 5m. Bài 111* trang 45 SBT Toán 12 Tập 1