Giải bài tập Bài 56 trang 25 SBT Toán 12 Tập 1 | SBT Toán 12 - Cánh diều (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 56 trang 25 SBT Toán 12 Tập 1. Bài 3. Đường tiệm cận của đồ thị hàm số.. SBT Toán 12 - Cánh diều (SBT)
Đề bài:
Cho hàm số y = f(x) liên tục trên ℝ và đồ thị có đường tiệm cận ngang như Hình 10. Hàm số y = f(x) có thể là hàm số nào trong các hàm số sau?
 A.
A.  .
.
B.  .
.
C.  .
.
D. 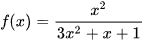 .
.
Đáp án và cách giải chi tiết:
Đáp án đúng là: A
Quan sát Hình 10, ta thấy đường thẳng y = 3 là đường tiệm cận ngang của đồ thị hàm số y = f(x).
Nhận thấy: 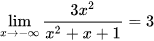 ;
; 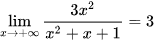 .
.
Do đó, đường thẳng y = 3 là đường tiệm cận ngang của đồ thị hàm số 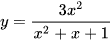 .
.
Vậy  .
.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 48 trang 23 SBT Toán 12 Tập 1
Tiệm cận đứng của đồ thị hàm số  là đường thẳng:
là đường thẳng:
A.  .
.
B. 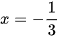 .
.
C.  .
.
D.  .
.
Bài 49 trang 23 SBT Toán 12 Tập 1
Tiệm cận ngang của đồ thị hàm số  là đường thẳng:
là đường thẳng:
A. 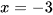 .
.
B. 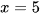 .
.
C.  .
.
D. 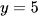 .
.
Bài 50 trang 23 SBT Toán 12 Tập 1
Tiệm cận đứng, tiệm cận ngang của đồ thị hàm số  là:
là:
A. Tiệm cận đứng là đường thẳng 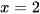 ; tiệm cận ngang là đường thẳng
; tiệm cận ngang là đường thẳng  .
.
B. Tiệm cận đứng là đường thẳng  ; tiệm cận ngang là đường thẳng
; tiệm cận ngang là đường thẳng  .
.
C. Tiệm cận đứng là đường thẳng 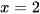 ; tiệm cận ngang là đường thẳng
; tiệm cận ngang là đường thẳng  .
.
C. Tiệm cận đứng là đường thẳng 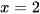 ; tiệm cận ngang là đường thẳng
; tiệm cận ngang là đường thẳng  .
.
Bài 51 trang 23 SBT Toán 12 Tập 1
Đồ thị hàm số nào sau đây nhận đường thẳng 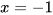 làm tiệm cận đứng?
làm tiệm cận đứng?
A.  .
.
B.  .
.
C.  .
.
D.  .
.
Bài 52 trang 23 SBT Toán 12 Tập 1
Tiệm cận xiên của đồ thị hàm số  là đường thẳng:
là đường thẳng:
A.  .
.
B.  .
.
C.  .
.
D.  .
.
Bài 53 trang 23 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
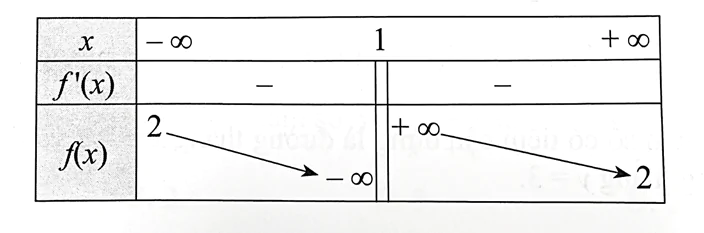
Tiệm cận đứng của đồ thị hàm số là đường thẳng:
A.  .
.
B.  .
.
C.  .
.
D. 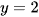 .
.
Bài 54 trang 24 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{−2}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
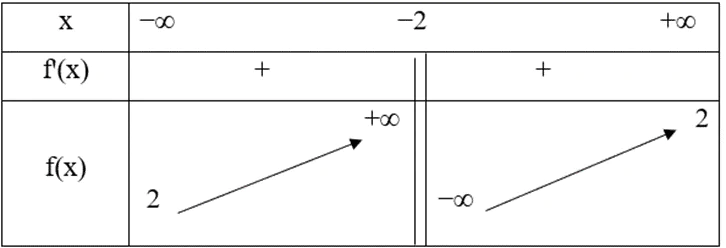
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng y = 2 và tiệm cận ngang là đường thẳng x = −2.
B. Đồ thị hàm số có tiệm cận đứng là đường thẳng y = −2 và tiệm cận ngang là đường thẳng x = 2.
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 2 và tiệm cận ngang là đường thẳng y = −2.
D. Đồ thị hàm số có tiệm cận đứng là đường thẳng x = −2 và tiệm cận ngang là đường thẳng y = 2.
Bài 55 trang 24 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{−2}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng x = −2 và không có tiệm cận ngang.
B. Đồ thị hàm số có tiệm cận đứng là đường thẳng x = −2 và tiệm cận ngang là đường thẳng y = 3.
C. Đồ thị hàm số không có tiệm cận đứng và tiệm cận ngang là đường thẳng y = −2.
D. Đồ thị hàm số có tiệm cận đứng là đường thẳng x = −2 và tiệm cận ngang là đường thẳng y = 3.
Bài 57 trang 25 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{1} và có đồ thị như Hình 11.
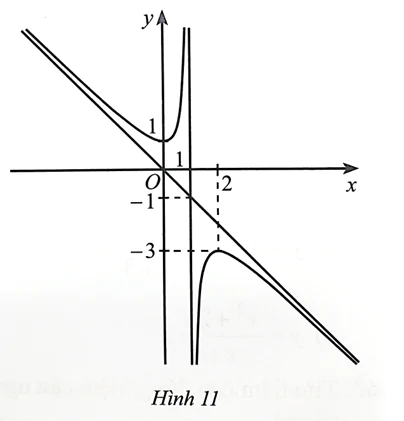
Các đường tiệm cận của đồ thị hàm số là:
A. Tiệm cận đứng là đường thẳng x = 1 và tiệm cận xiên là đường thẳng y = −x.
B. Tiệm cận đứng là đường thẳng x = −1 và tiệm cận xiên là đường thẳng y = x.
C. Tiệm cận đứng là đường thẳng x = 1 và tiệm cận xiên là đường thẳng y = x.
D. Tiệm cận đứng là đường thẳng x = 1 và tiệm cận xiên là đường thẳng y = −2x.
Bài 58 trang 25 SBT Toán 12 Tập 1
Giao điểm I của hai đường tiệm cận của đồ thị hàm số  là:
là:
A. 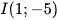 .
.
B.  .
.
C. 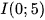 .
.
D.  .
.
Bài 59 trang 25 SBT Toán 12 Tập 1
Số đường tiệm cận của đồ thị hàm số 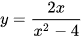 là:
là:
A. 1.
B. 2.
C. 3.
D. 0.
Bài 60 trang 25 SBT Toán 12 Tập 1
Số đường tiệm cận của đồ thị hàm số  là:
là:
A. 1.
B. 2.
C. 3.
D. 0.
Bài 61 trang 26 SBT Toán 12 Tập 1
Số đường tiệm cận của đồ thị hàm số  là:
là:
A. 1.
B. 2.
C. 3.
D. 4.
Bài 62 trang 26 SBT Toán 12 Tập 1
Cho hàm số 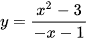 .
.
a) Đồ thị hàm số có tiệm cận đứng là đường thẳng  .
. ![]()
![]()
b) Đồ thị hàm số có tiệm cận ngang là đường thẳng 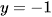 .
. ![]()
![]()
c) Đồ thị hàm số có tiệm cận xiên là đường thẳng  .
. ![]()
![]()
d) Giao điểm I của hai đường tiệm cận của đồ thị hàm số là  .
. ![]()
![]()
Bài 63 trang 26 SBT Toán 12 Tập 1
Tìm tiệm cận đứng, tiệm cận ngang của đồ thị mỗi hàm số sau:
a)  ;
;
b)  ;
;
c) 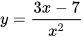 ;
;
d) 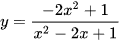 .
.
Bài 64 trang 26 SBT Toán 12 Tập 1
Tìm tiệm cận đứng, tiệm cận xiên của đồ thị mỗi hàm số sau:
a) 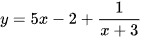 ;
;
b)  ;
;
c) 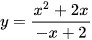 ;
;
d) 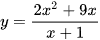 .
.
Bài 65 trang 26 SBT Toán 12 Tập 1
Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:
a)
b) 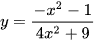 ;
;
c) 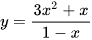 .
.
Bài 66 trang 26 SBT Toán 12 Tập 1
Tốc độ đánh máy trung bình S (tính bằng từ trên phút) của một học viên sau t tuần học được cho bởi công thức:
 với
với  .
.
a) Xem  là một hàm số xác định trên khoảng
là một hàm số xác định trên khoảng  , hãy tìm tiệm cận ngang của đồ thị hàm số đó.
, hãy tìm tiệm cận ngang của đồ thị hàm số đó.
b) Nêu nhận xét về tốc độ đánh máy trung bình của học viên đó khi thời gian t càng lớn.
Bài 67 trang 27 SBT Toán 12 Tập 1
Tổng chi phí để sản xuất x sản phẩm của một xí nghiệp được tính theo công thức
T = 20x + 100 000 (nghìn đồng).
a) Viết công thức tính chi phí trung bình C(x) của một sản phẩm khi sản xuất được x sản phẩm.
b) Xem y = C(x) là một hàm số xác định trên khoảng  , hãy tìm tiệm cận ngang của đồ thị hàm số đó.
, hãy tìm tiệm cận ngang của đồ thị hàm số đó.
c) Xét tính đơn điệu của hàm số y = C(x) trên khoảng  .
.
d) Nêu nhận xét về chi phí để tạo ra 1 sản phẩm khi x càng lớn.
 ;
;