Giải bài tập Toán 12 Bài 1. Tính đơn điệu của hàm số. | Cánh Diều
Hướng dẫn giải chi tiết Bài 1. Tính đơn điệu của hàm số. Liên hệ giữa đạo hàm và tính đồng biến, nghịch biến của hàm số
Bài 1 trang 10 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm f'(x) như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.  .
.
B.  .
.
C.  .
.
D.  .
.
Bài 2 trang 10 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. 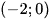 .
.
B.  .
.
C.  .
.
D.  .
.
Bài 3 trang 10 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm  ,
,  . Khẳng định nào dưới đây đúng?
. Khẳng định nào dưới đây đúng?
A.  .
.
B.  .
.
C.  .
.
D. 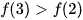 .
.
Bài 4 trang 11 SBT Toán 12 Tập 1
Cho hàm số  . Mệnh đề nào dưới đây là đúng?
. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên khoảng  .
.
B. Hàm số nghịch biến trên khoảng  .
.
C. Hàm số đồng biến trên khoảng 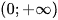 .
.
D. Hàm số nghịch biến trên khoảng 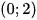 .
.
Bài 5 trang 11 SBT Toán 12 Tập 1
Cho hàm số  . Mệnh đề nào dưới đây là đúng?
. Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên khoảng  và
và  .
.
B. Hàm số nghịch biến trên ℝ.
C. Hàm số đồng biến trên ℝ.
D. Hàm số nghịch biến trên khoảng  và
và  .
.
Bài 6 trang 11 SBT Toán 12 Tập 1
Trong các hàm số sau, hàm số đồng biến trên ℝ là:
A.  .
.
B.  .
.
C. 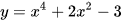 .
.
D. 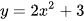 .
.
Bài 7 trang 11 SBT Toán 12 Tập 1
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 4. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A.  .
.
B. 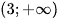 .
.
C.  .
.
D.  .
.
Bài 8 trang 11 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm trên ℝ và bảng xét dấu của đạo hàm như sau:

Số điểm cực trị của hàm số đã cho là:
A. 0.
B. 1.
C. 2.
D. 3.
Bài 9 trang 12 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có bảng biến thiên như sau:

Điểm cực đại của hàm số đã cho là:
A. −1.
B. 3.
C. 2.
D. 0.
Bài 10 trang 12 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có bảng biến thiên như sau:
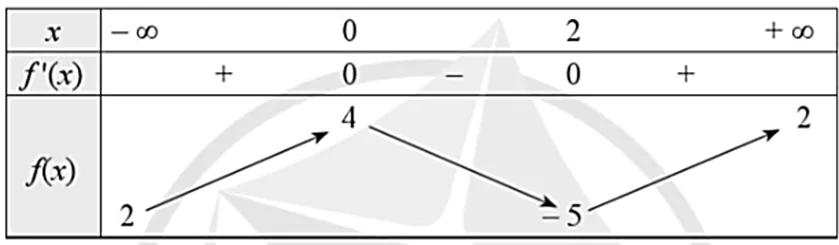
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại  .
.
B. Hàm số có giá trị cực đại bằng 0.
C. Hàm số đạt cực tiểu tại 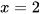 .
.
D. Hàm số đạt cực đại tại  .
.
Bài 11 trang 12 SBT Toán 12 Tập 1
Cho hàm số f(x) có đạo hàm 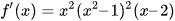 ,
,  . Số điểm cực trị của hàm số đã cho là:
. Số điểm cực trị của hàm số đã cho là:
A. 1.
B. 2.
C. 3.
D. 4.
Bài 12 trang 12 SBT Toán 12 Tập 1
Cho hàm số  . Kết luận nào sau đây đúng?
. Kết luận nào sau đây đúng?
A. Hàm số có 3 cực trị.
B. Hàm số có 2 cực trị.
C. Hàm số có 1 cực trị.
D. Hàm số không có cực trị.
Bài 13 trang 12 SBT Toán 12 Tập 1
Hàm số 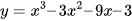 đạt cực tiểu tại điểm:
đạt cực tiểu tại điểm:
A. −1.
B. 3.
C. 2.
D. −30.
Bài 14 trang 12 SBT Toán 12 Tập 1
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 5. Số điểm cực trị của hàm số đã cho là:

A. 2.
B. 4.
C. 1.
D. 3.
Bài 15 trang 13 SBT Toán 12 Tập 1
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là:

A. 2.
B. 1.
C. −1.
D. 0.
Bài 16 trang 13 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm trên ℝ và đồ thị hàm số y = f'(x) như Hình 7. Số điểm cực trị của hàm số y = f(x) là:

A. 4.
B. 3.
C. 2.
D. 1.
Bài 17 trang 13 SBT Toán 12 Tập 1
Cho hàm số y = x3 – 3x + 2.
a)  .
. ![]()
![]()
b) y' = 0 khi x = −1, x = 1. ![]()
![]()
c) y' > 0 khi  và y' < 0 khi
và y' < 0 khi  .
. ![]()
![]()
d) Giá trị cực đại của hàm số là  .
. ![]()
![]()
Bài 18 trang 13 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm trên ℝ và đồ thị hàm số của y = f'(x) như Hình 8.
 a)
a)  khi
khi  ,
, 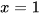 ,
,  .
. ![]()
![]()
b) Hàm số  đồng biến trên khoảng
đồng biến trên khoảng 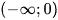 .
. ![]()
![]()
c)  khi
khi  .
. ![]()
![]()
d) Hàm số  đồng biến trên
đồng biến trên 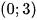 .
. ![]()
![]()
Bài 19 trang 14 SBT Toán 12 Tập 1
Tìm các khoảng đơn điệu của mỗi hàm số sau:
a)  ;
;
b)  ;
;
c) 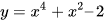 ;
;
d) 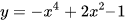 ;
;
e) 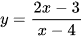 ;
;
g)  .
.
Bài 20 trang 14 SBT Toán 12 Tập 1
Tìm điểm cực trị của mỗi hàm số sau:
a) 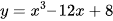 ;
;
b)  ;
;
c) 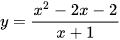 ;
;
d) 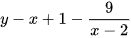 .
.
Bài 21 trang 14 SBT Toán 12 Tập 1
Dùng đạo hàm của hàm số, hãy giải thích:
a) Hàm số  đồng biến trên ℝ khi a > 1, nghịch biến trên ℝ khi 0 < a < 1.
đồng biến trên ℝ khi a > 1, nghịch biến trên ℝ khi 0 < a < 1.
b) Hàm số  đồng biến trên khoảng
đồng biến trên khoảng  khi a > 1, nghịch biến trên khoảng
khi a > 1, nghịch biến trên khoảng  khi 0 < a < 1.
khi 0 < a < 1.
Bài 22 trang 14 SBT Toán 12 Tập 1
Chứng minh rằng:
a) Hàm số  nghịch biến trên khoảng
nghịch biến trên khoảng  và đồng biến trên khoảng
và đồng biến trên khoảng  .
.
b) Hàm số  nghịch biến trên khoảng
nghịch biến trên khoảng  và đồng biến trên khoảng
và đồng biến trên khoảng  .
.
c) Hàm số 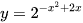 đồng biến trên khoảng
đồng biến trên khoảng  và nghịch biến trên khoảng
và nghịch biến trên khoảng 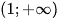 .
.
Bài 23 trang 14 SBT Toán 12 Tập 1
Tìm điểm cực trị của mỗi hàm số sau:
a) 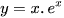 ;
;
b)  ;
;
c)  ;
;
d)  .
.
Bài 24 trang 14 SBT Toán 12 Tập 1
Trong một thí nghiệm y học, người ta cấy 1 000 con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức:
 trong đó t là thời gian tính bằng giây
trong đó t là thời gian tính bằng giây 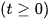 (Nguồn R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Trong khoảng thời gian nào từ lúc nuôi cấy, lượng vi khuẩn sẽ tăng lên?
(Nguồn R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Trong khoảng thời gian nào từ lúc nuôi cấy, lượng vi khuẩn sẽ tăng lên?
Bài 25 trang 15 SBT Toán 12 Tập 1
Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình

trong đó t tính bằng giây và s tính bằng mét. Trong khoảng thời gian nào của 5 giây đầu tiên thì vận tốc tức thời của chất điểm tăng lên?