Giải bài tập Bài 102 trang 43 SBT Toán 12 Tập 1 | SBT Toán 12 - Cánh diều (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 102 trang 43 SBT Toán 12 Tập 1. Bài tập cuối chương 1. SBT Toán 12 - Cánh diều (SBT)
Đề bài:
Cho hàm số bậc ba 
có đồ thị là đường cong như Hình 30.
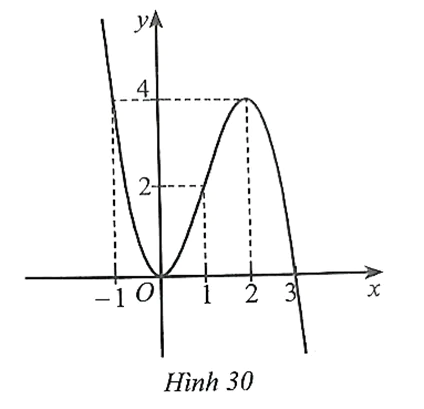a) Phương trình 
có hai nghiệm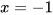 
, 
. 
b) Phương trình 
có hai nghiệm.
c) Phương trình 
có ba nghiệm.
d) Phương trình 
có sáu nghiệm.
Đáp án và cách giải chi tiết:
|
a) Đ |
b) S |
c) Đ |
d) S |
Dựa vào đồ thị hàm số Hình 30, ta có:
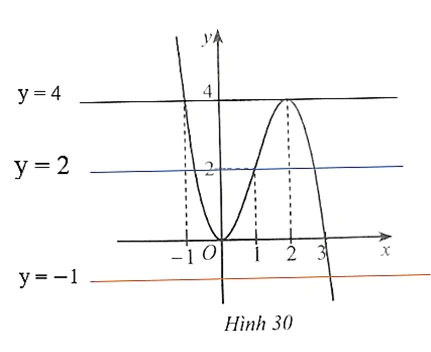
Đường thẳng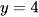 
cắt đồ thị hàm số y = f(x) tại hai điểm có hoành độ bằng −1 và 2 nên phương trình 
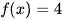có hai nghiệm phân biệt là 
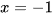và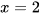 
.
Đường thẳng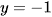 
cắt đồ thị hàm số 
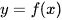tại một điểm nên phương trình 
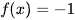có một nghiệm.
Đường thẳng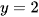 
cắt đồ thị hàm số 
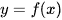tại ba điểm nên phương trình 
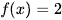có ba nghiệm.
Ta có: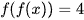 
khi 
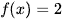hoặc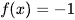 
.
Với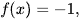 
phương trình có một nghiệm.
Với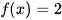 
phương trình có ba nghiệm.
Vậy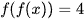 
có 4 nghiệm.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 83 trang 39 SBT Toán 12 Tập 1
Cho hàm số f(x) xác định trên ℝ có bảng xét dấu đạo hàm f'(x) như sau:
Khẳng định nào dưới đây là đúng?
A. 
.
B.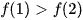 
.
C. 
.
D. 
.
Bài 84 trang 39 SBT Toán 12 Tập 1
Kết luận nào sau đây là đúng đối với hàm số 
?
A. Hàm số đồng biến trên ℝ.
B. Hàm số nghịch biến trên ℝ.
C. Hàm số đồng biến trên khoảng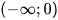 
và nghịch biến trên khoảng 
.
D. Hàm số nghịch biến trên khoảng 
và đồng biến trên khoảng 
.
Bài 85 trang 39 SBT Toán 12 Tập 1
Trong các hàm số sau, hàm số nghịch biến trên ℝ là:
A. 
.
B. 
.
C. 
.
D. 
.
Bài 86 trang 39 SBT Toán 12 Tập 1
Cho hàm số bậc ba 
có đồ thị là đường cong như Hình 25. Hàm số đã cho đồng biến trên khoảng nào sau đây?
A. 
.
B. 
.
C. 
.
D. 
.
Bài 87 trang 40 SBT Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ có bảng biến thiên như sau:
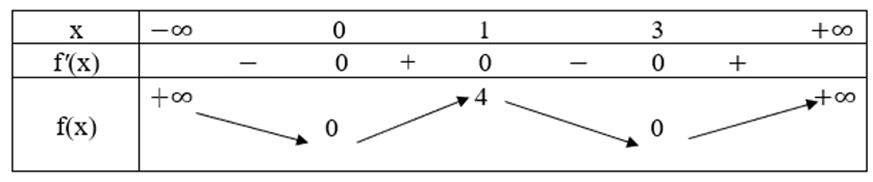
Số điểm cực trị của hàm số là:
A. 0.
B. 1.
C. 2.
D. 3.
Bài 88 trang 40 SBT Toán 12 Tập 1
Cho hàm số f(x) có đạo hàm 
, 
. Điểm cực đại của hàm số đã cho là:
A. −1.
B. −2.
C. 2.
D. 1.
Bài 89 trang 40 SBT Toán 12 Tập 1
Cho hàm số 
(với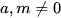 
) có đồ thị là đường cong như Hình 26.
Giá trị cực đại của hàm số là:
A. 0.
B. −1.
C. 2.
D. 3.
Bài 90 trang 40 SBT Toán 12 Tập 1
Giá trị nhỏ nhất của hàm số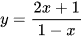 
trên đoạn [2; 3] bằng:
A. −5.
B. −2.
C. 0.
D. 1.
Bài 91 trang 40 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số 
bằng:
A. 
.
B. 
.
C. 1.
D. 2.
Bài 92 trang 40 SBT Toán 12 Tập 1
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 
trên đoạn 
lần lượt là:
A. 
.
B.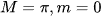 
.
C. 
,
D. 
.
Bài 93 trang 41 SBT Toán 12 Tập 1
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 
trên đoạn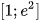 
bằng:
A. 
.
B. 
.
C. 
.
D. 
.
Bài 94 trang 41 SBT Toán 12 Tập 1
Đồ thị hàm số nào sau đây nhận đường thẳng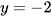 
làm tiệm cận ngang?
A. 
.
B.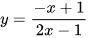 
,
C.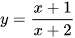 
.
D. 
.
Bài 95 trang 41 SBT Toán 12 Tập 1
Đường tiệm cận xiên của đồ thị hàm số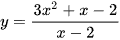 
là đường thẳng:
A. 
.
B. 
.
C. 
.
D. 
.
Bài 96 trang 41 SBT Toán 12 Tập 1
Đường cong ở Hình 27 là đồ thị của hàm số:
A. 
.
B. 
.
C. 
.
D. 
.
Bài 97 trang 41 SBT Toán 12 Tập 1
Đường cong ở Hình 28 là đồ thị của hàm số:
A. 
.
B.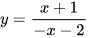 
.
C. 
.
D.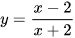 
.
Bài 98 trang 42 SBT Toán 12 Tập 1
Đường cong ở Hình 29 là đồ thị của hàm số:
A.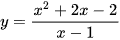 
.
B. 
.
C.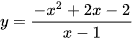 
.
D. 
.
Bài 99 trang 42 SBT Toán 12 Tập 1
Cho hàm số 
.
a) 
. 
b) 
khi 
.
c) 
khi 
và 
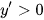khi 
.
d) Hàm số đạt cực đại tại 
.
Bài 99 trang 42 SBT Toán 12 Tập 1
Cho hàm số .
a) .
b) khi .
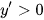c) khi và khi .
d) Hàm số đạt cực đại tại .
Bài 100 trang 42 SBT Toán 12 Tập 1
Cho hàm số 
.
a) 
. 
b)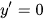 
khi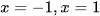 
.
c) 
.
d) Trên đoạn 
, hàm số đạt giá trị nhỏ nhất bằng 1, giá trị lớn nhất bằng 8.
Bài 101 trang 42 SBT Toán 12 Tập 1
Cho hàm số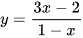 
.
a) Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1. 
b) Đồ thị hàm số có tiệm cận ngang là đường thẳng y = 3.
c) Điểm M nằm trên đồ thị hàm số có hoành độ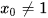 
thì tung độ 
.
d) Tích khoảng cách từ điểm M bất kì nằm trên đồ thị hàm số đến hai đường tiệm cận của đồ thị hàm số đó bằng 1.