Giải bài tập Toán 9 Chương 9. Đường tròn ngoại tiếp và đường tròn nội tiếp | Kết Nối Tri Thức
Hướng dẫn giải chi tiết Chương 9. Đường tròn ngoại tiếp và đường tròn nội tiếp. Đường tròn đi qua đỉnh tam giác, tứ giác hay lục giác. Những đường tròn lớn nhất có thể vẽ được nằm bên trong hình đó.
Giải bài tập Bài 27. Góc nội tiếp
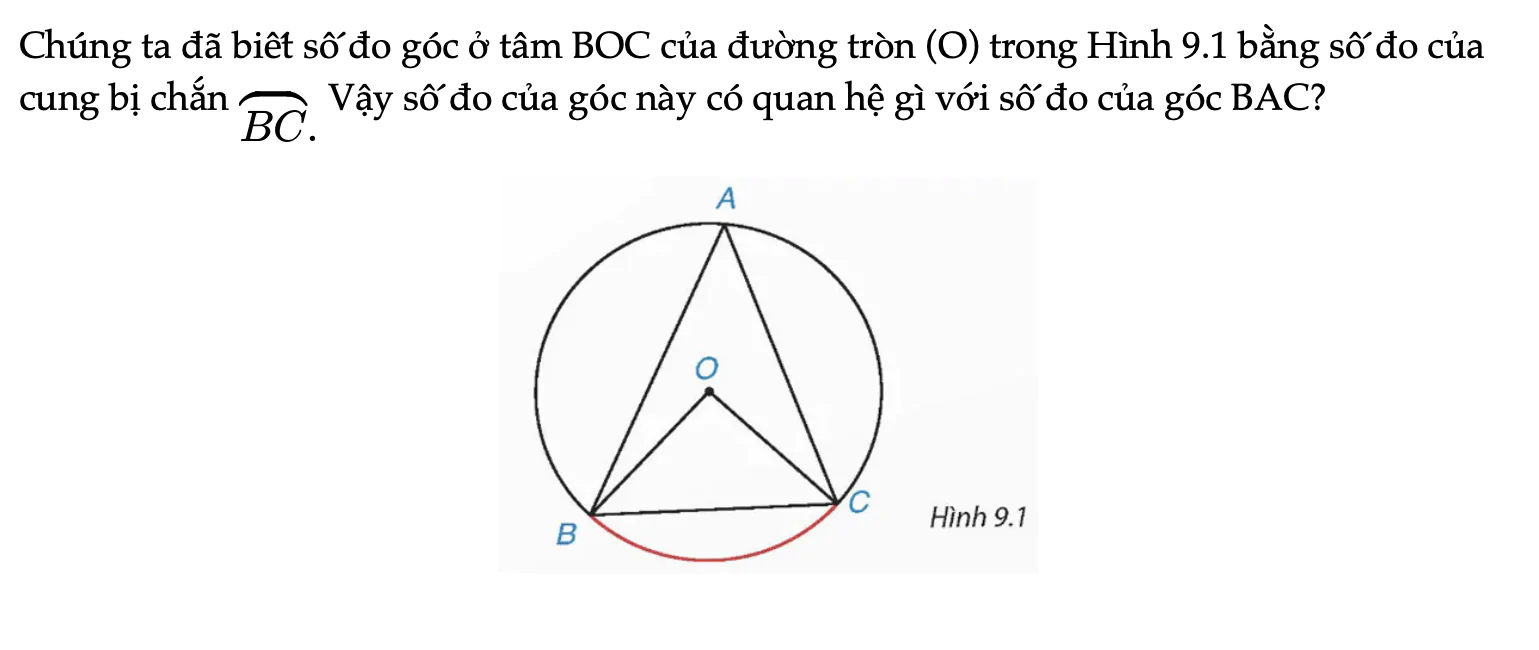
Mở đầu trang 67 Toán 9 Tập 2
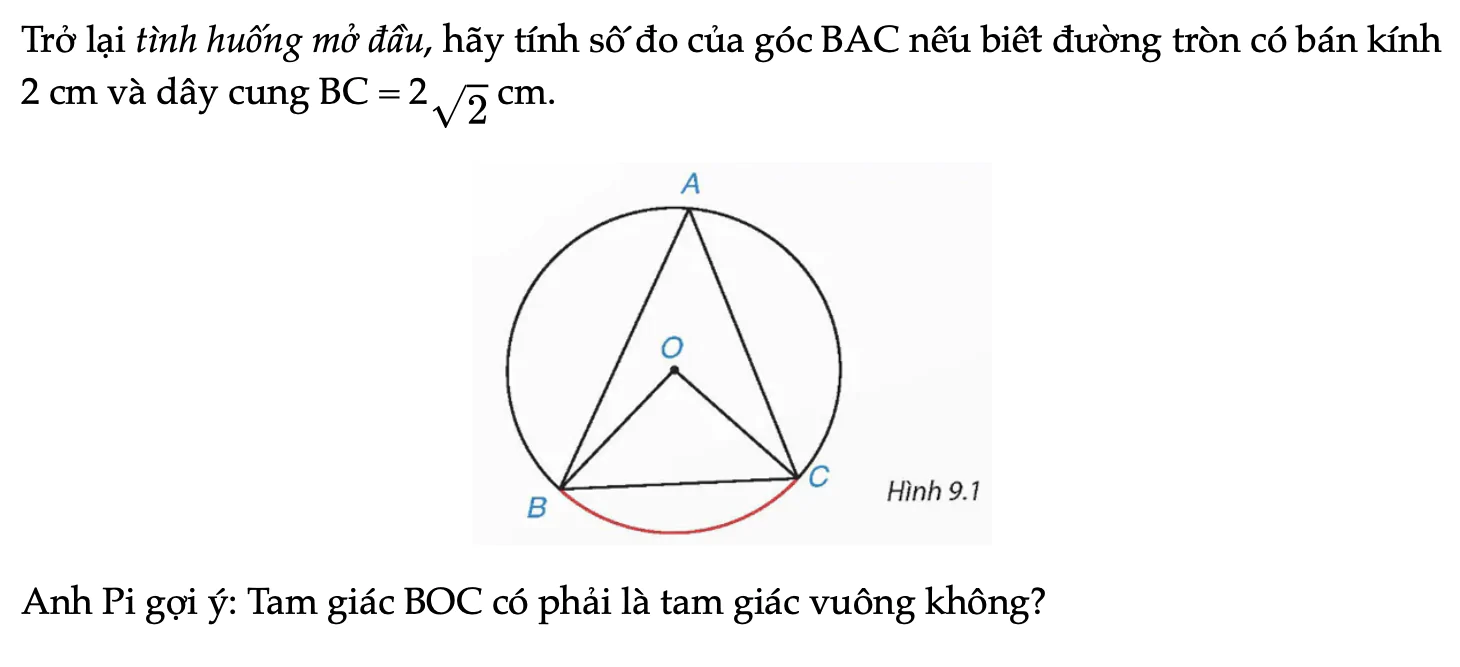
Chúng ta đã biết số đo góc ở tâm BOC của đường tròn (O) trong Hình 9.1 bằng số đo của cung bị chắn BC. Vậy số đo của góc này có quan hệ gì với số đo của góc BAC?
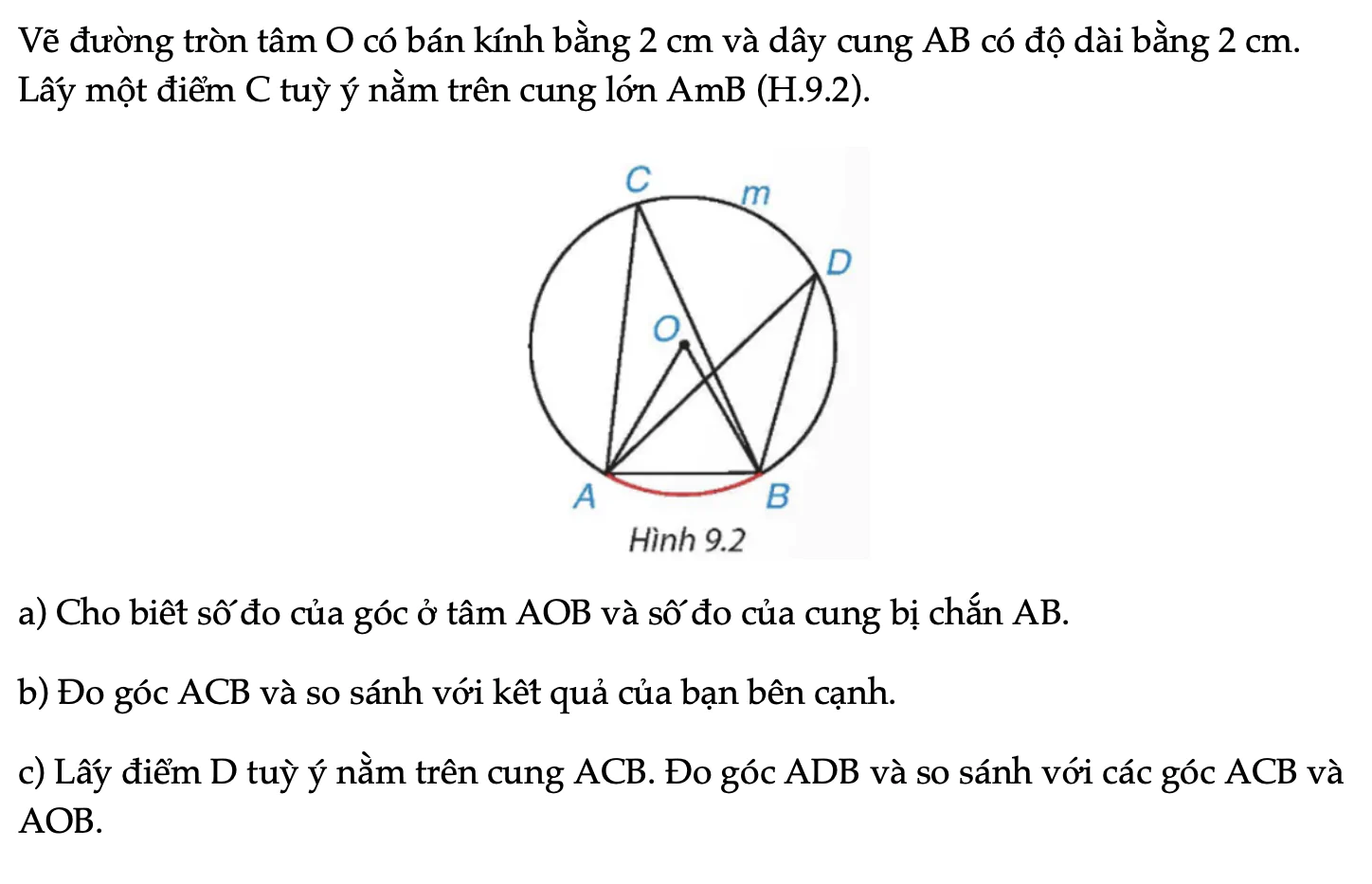
HĐ trang 68 Toán 9 Tập 2
Vẽ đường tròn tâm O có bán kính bằng 2 cm và dây cung AB có độ dài bằng 2 cm. Lấy một điểm C tuỳ ý nằm trên cung lớn AmB (H.9.2).
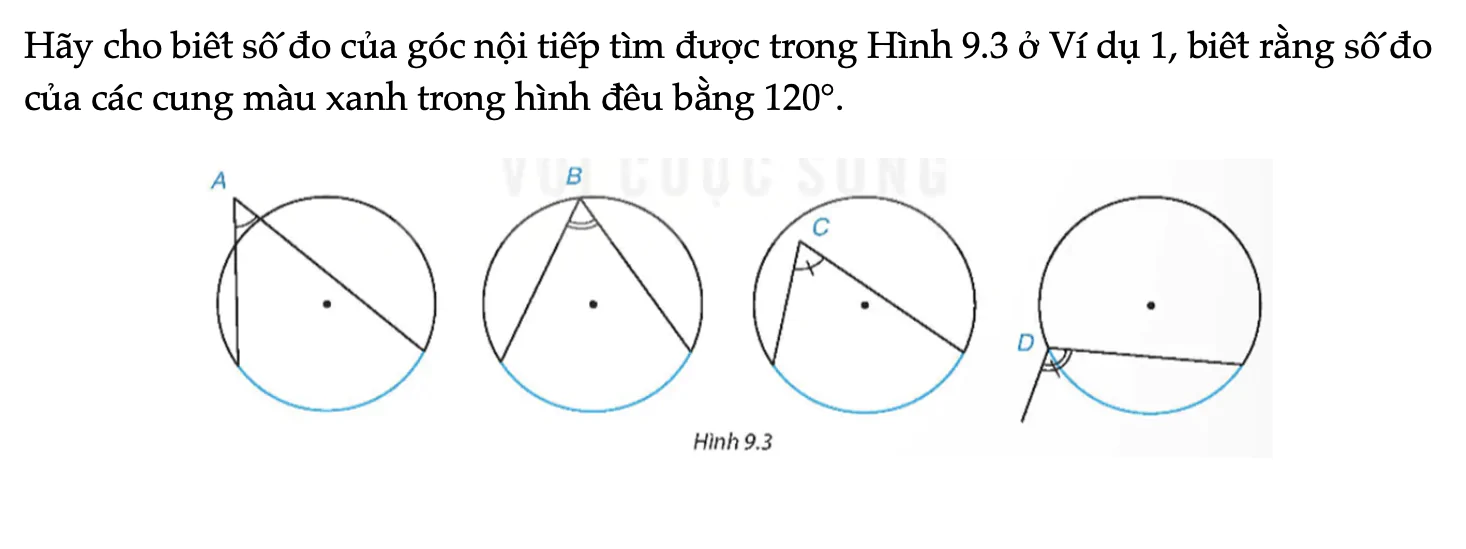
Câu hỏi trang 70 Toán 9 Tập 2
Hãy cho biết số đo của góc nội tiếp tìm được trong Hình 9.3 ở Ví dụ 1, biết rằng số đo của các cung màu xanh trong hình đều bằng 120°.
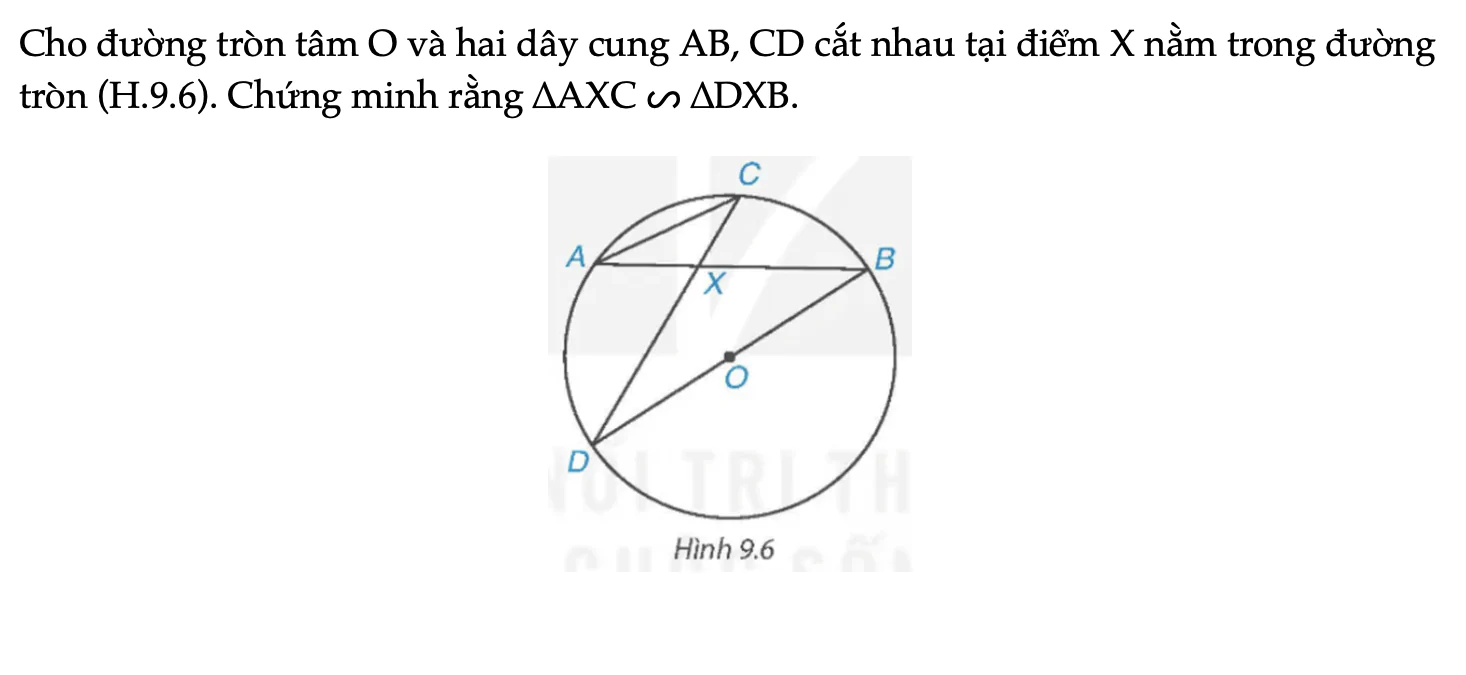
Luyện tập trang 70 Toán 9 Tập 2
Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng ∆AXC ᔕ ∆DXB.
Vận dụng trang 70 Toán 9 Tập 2
Trở lại tình huống mở đầu, hãy tính số đo của góc BAC nếu biết đường tròn có bán kính 2 cm và dây cung BC = 2√2 cm.

Bài 9.1 trang 70 Toán 9 Tập 2
Những khẳng định nào sau đây là đúng?
Bài 9.2 trang 71 Toán 9 Tập 2
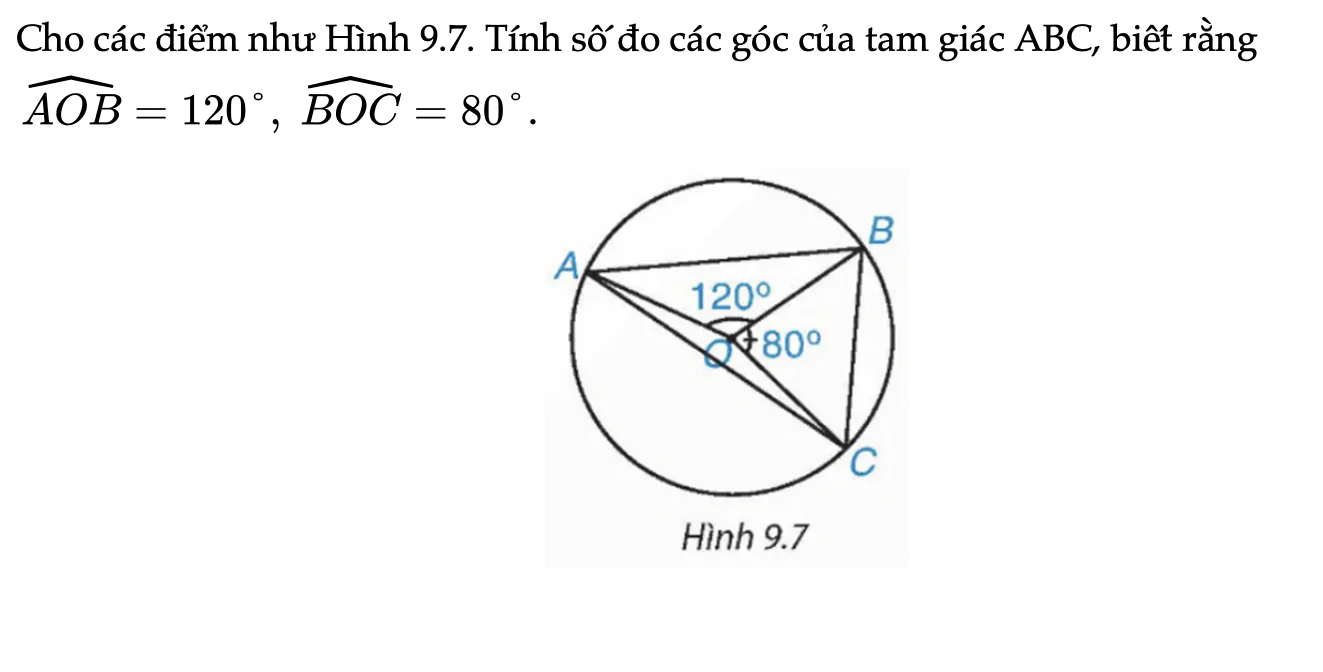
Cho các điểm như Hình 9.7. Tính số đo các góc của tam giác ABC, biết rằng góc AOB=120°, góc BOC=80°.
Bài 9.3 trang 71 Toán 9 Tập 2
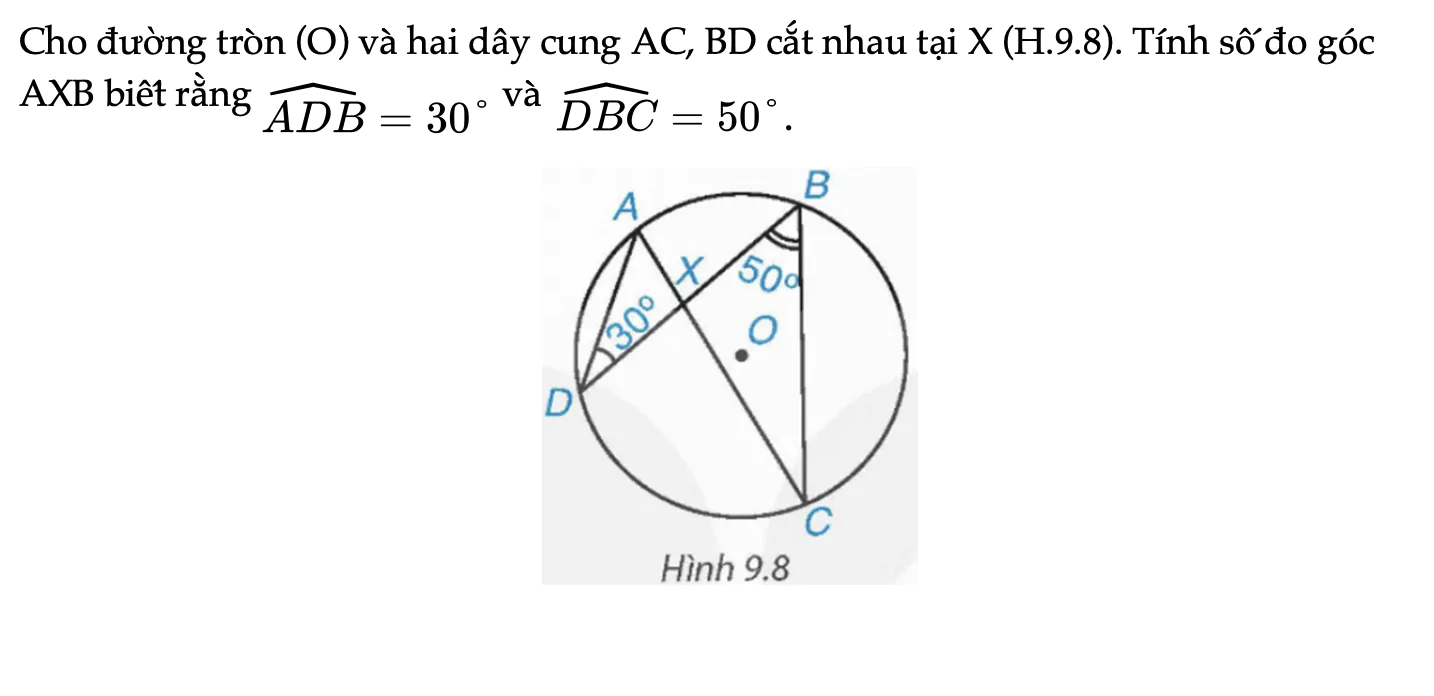
Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X (H.9.8). Tính số đo góc AXB.
Bài 9.4 trang 71 Toán 9 Tập 2
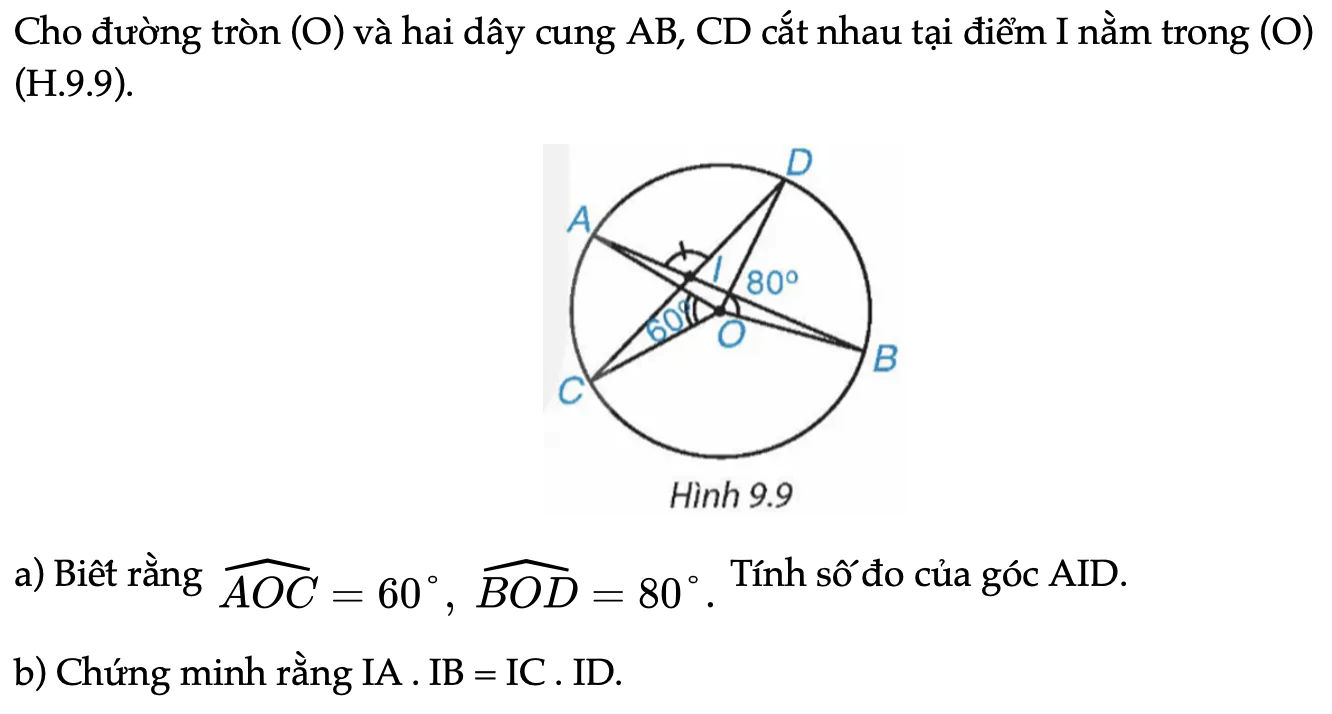
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) (H.9.9).
Bài 9.5 trang 71 Toán 9 Tập 2
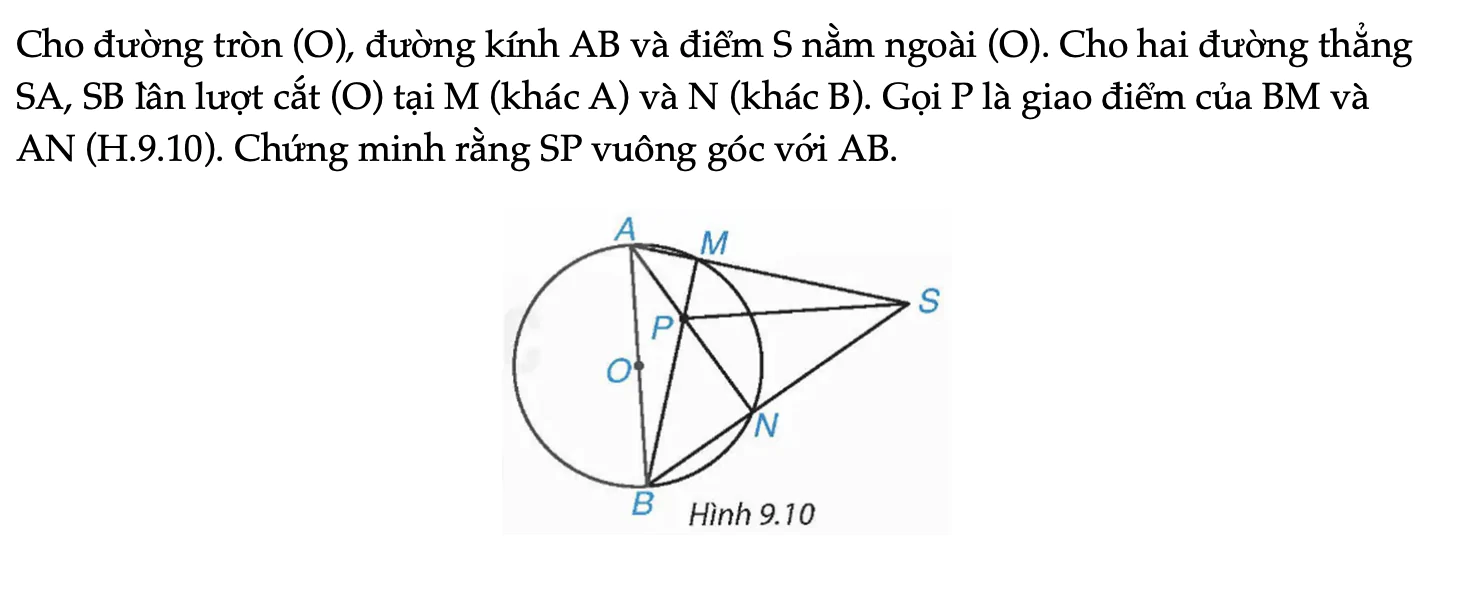
Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A) và N (khác B). Gọi P là giao điểm của BM và AN (H.9.10). Chứng minh rằng SP vuông góc với AB.

Bài 9.6 trang 71 Toán 9 Tập 2
Trên sân bóng, khi quả bóng được đặt tại điểm phạt đền thì có góc sút bằng 36° và quả bóng cách mỗi cọc gôn 11,6 m (H.9.11). Hỏi khi quả bóng đặt ở vị trí cách điểm phạt đến 11,6 m thì góc sút bằng bao nhiêu?
Giải bài tập Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác

Mở đầu trang 72 Toán 9 Tập 2:
Cho trước một tam giác ABC. Bằng thước kẻ và compa, em có thể vẽ được một đường tròn đi qua ba đỉnh của tam giác và đường tròn tiếp xúc với cả ba cạnh của tam giác hay không?
HĐ1 trang 72 Toán 9 Tập 2
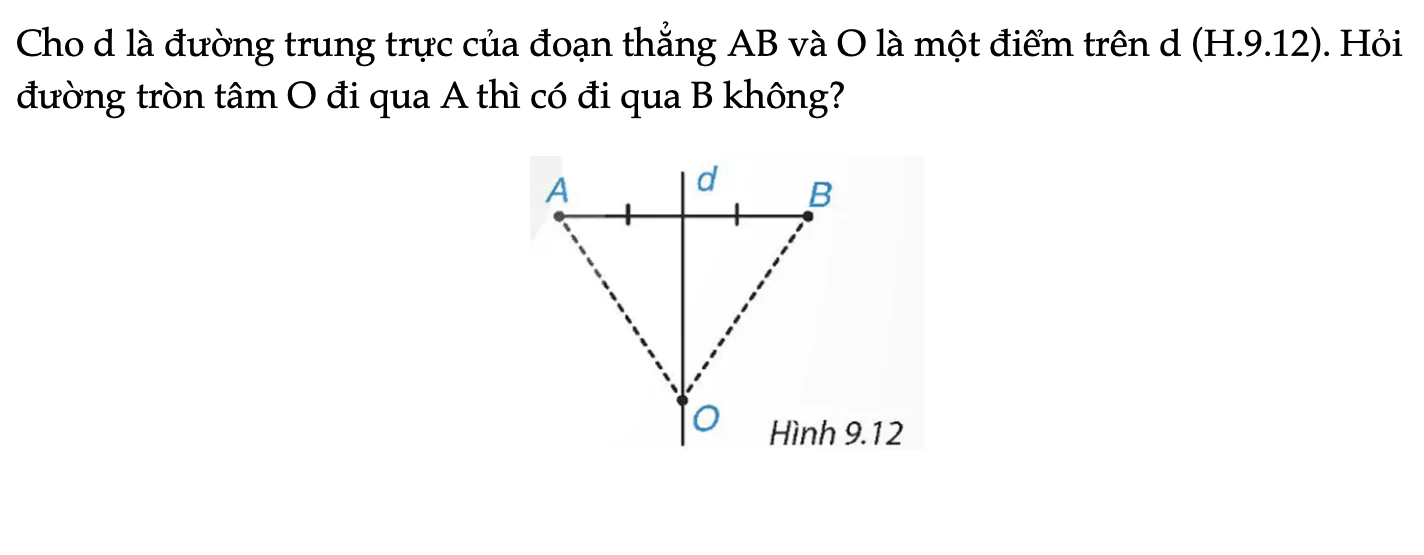
Cho d là đường trung trực của đoạn thẳng AB và O là một điểm trên d (H.9.12). Hỏi đường tròn tâm O đi qua A thì có đi qua B không?
HĐ2 trang 72 Toán 9 Tập 2
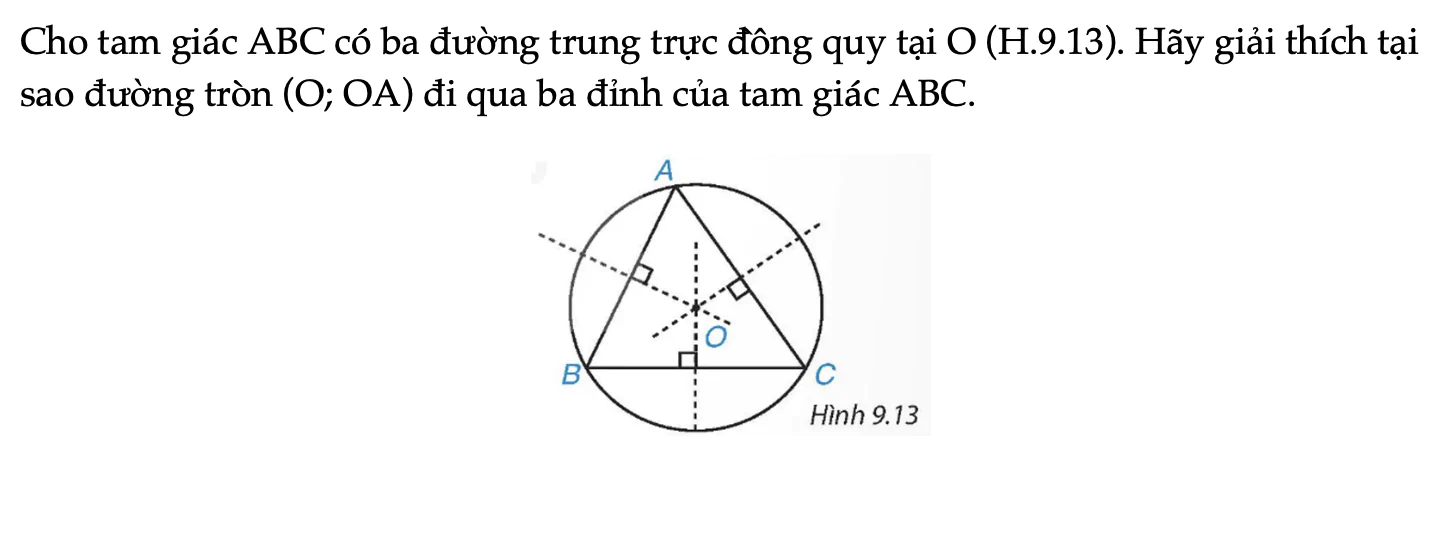
Cho tam giác ABC có ba đường trung trực đồng quy tại O (H.9.13). Hãy giải thích tại sao đường tròn (O; OA) đi qua ba đỉnh của tam giác ABC.
Câu hỏi trang 73 Toán 9 Tập 2
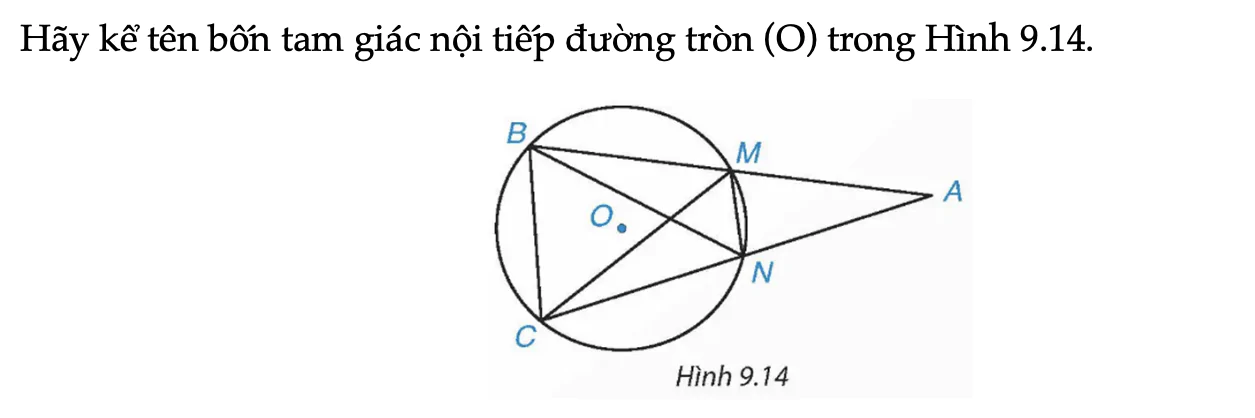
Hãy kể tên bốn tam giác nội tiếp đường tròn (O) trong Hình 9.14.
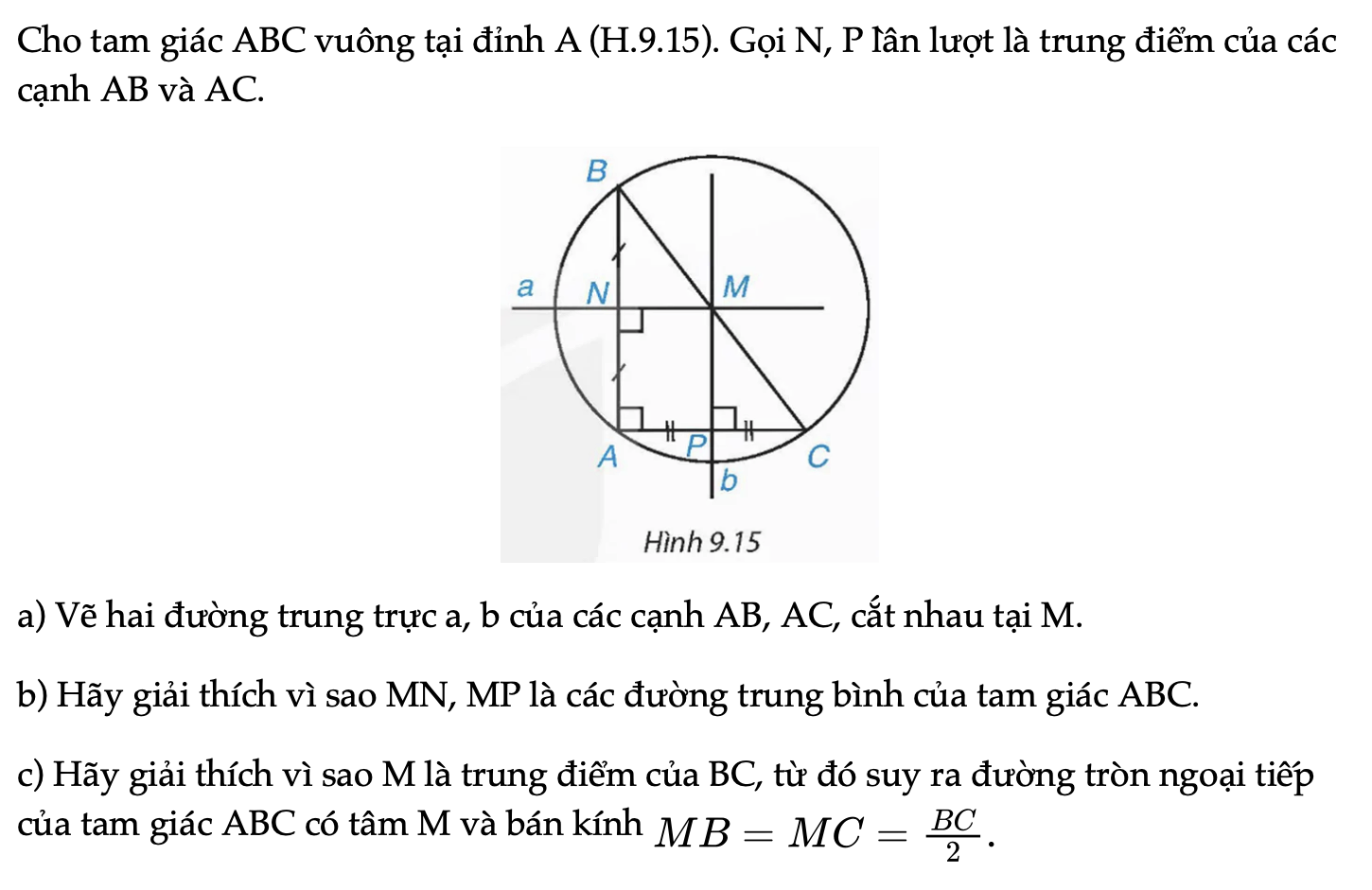
HĐ3 trang 73 Toán 9 Tập 2
Cho tam giác ABC vuông tại đỉnh A (H.9.15). Gọi N, P lần lượt là trung điểm của các cạnh AB và AC.
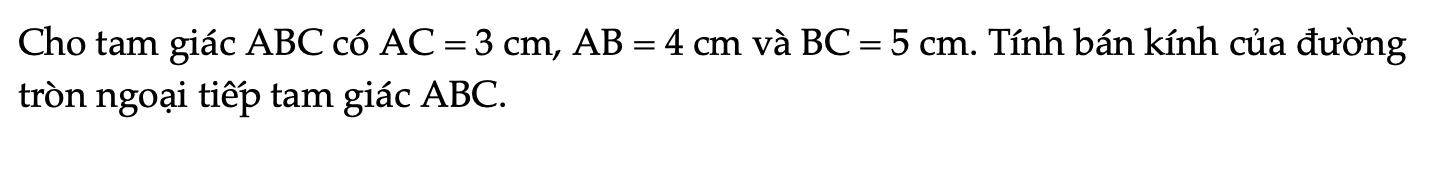
Luyện tập 1 trang 73 Toán 9 Tập 2
Cho tam giác ABC có AC = 3 cm, AB = 4 cm và BC = 5 cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
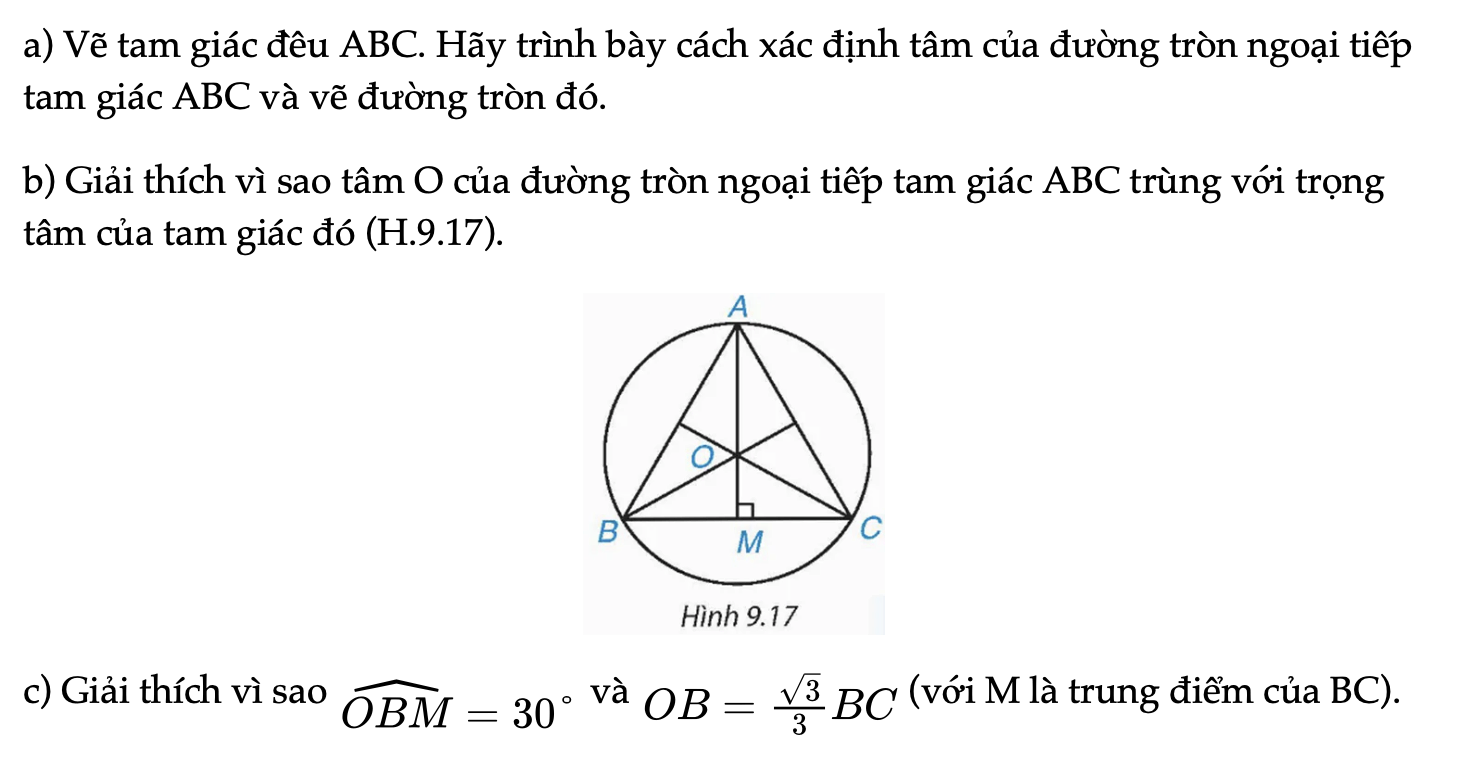
HĐ4 trang 73 Toán 9 Tập 2
a) Vẽ tam giác đều ABC. Hãy trình bày cách xác định tâm của đường tròn ngoại tiếp tam giác ABC và vẽ đường tròn đó. b) Giải thích vì sao tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó (H.9.17).
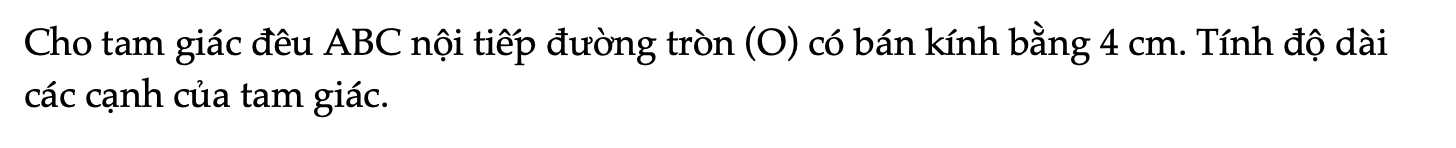
Luyện tập 2 trang 74 Toán 9 Tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O) có bán kính bằng 4 cm. Tính độ dài các cạnh của tam giác.
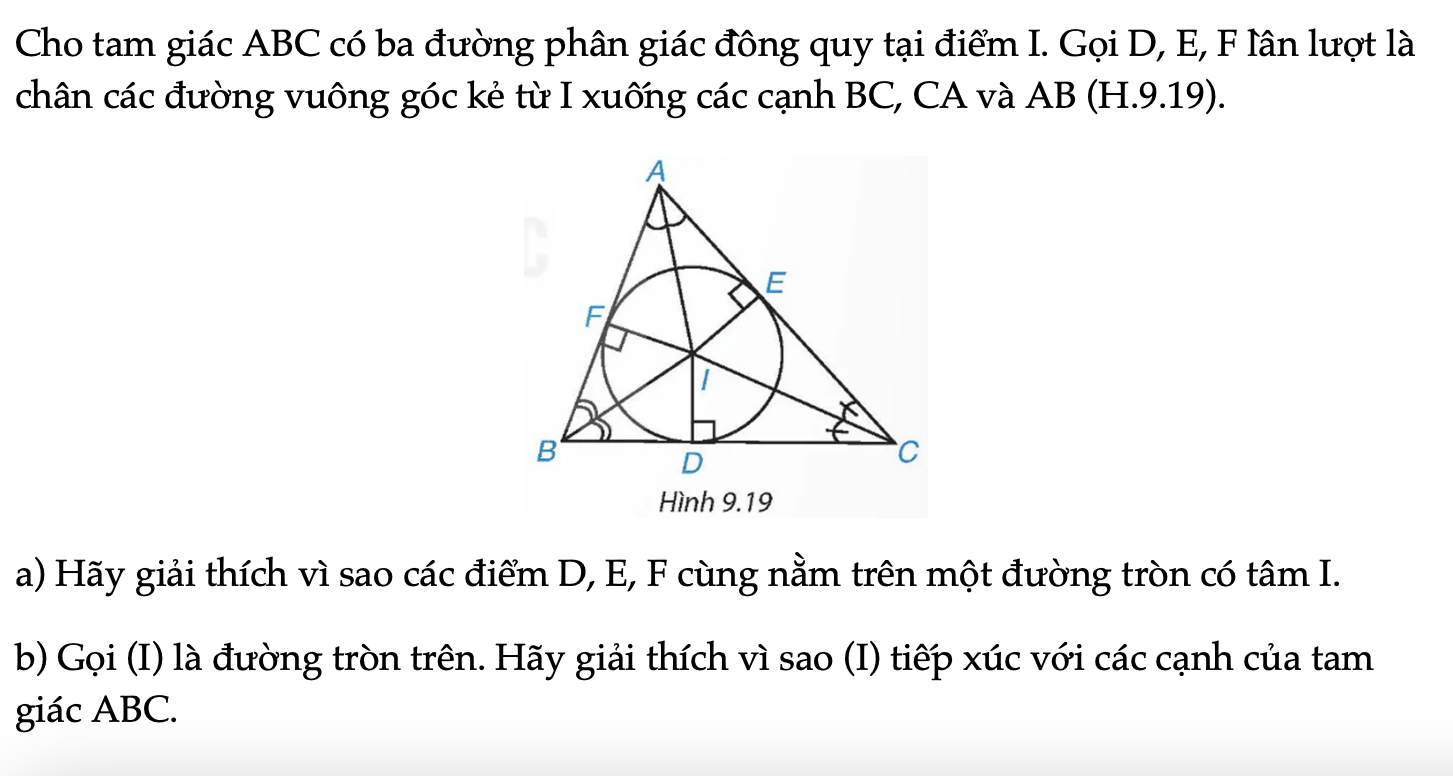
HĐ5 trang 74 Toán 9 Tập 2
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).
Câu hỏi trang 75 Toán 9 Tập 2
Mỗi tam giác có bao nhiêu đường tròn nội tiếp? Có bao nhiêu tam giác cùng ngoại tiếp một đường tròn?

HĐ6 trang 75 Toán 9 Tập 2
Cho tam giác đều ABC có trọng tâm G. a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC. b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa bán kính đường tròn ngoại tiếp tam giác ABC và bằng √3/6BC.
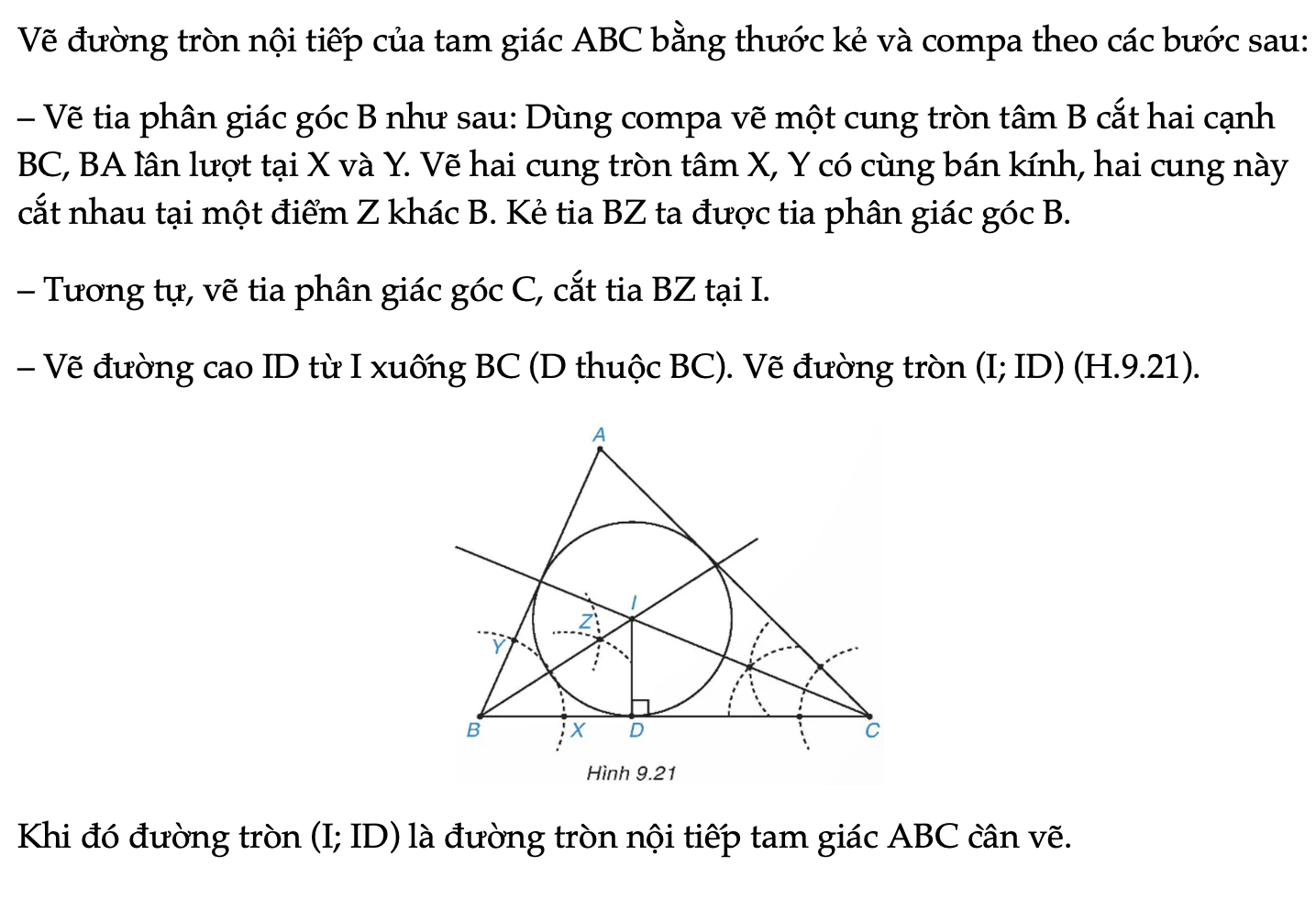
Thực hành trang 75 Toán 9 Tập 2
Vẽ đường tròn nội tiếp của tam giác ABC bằng thước kẻ và compa theo các bước sau.
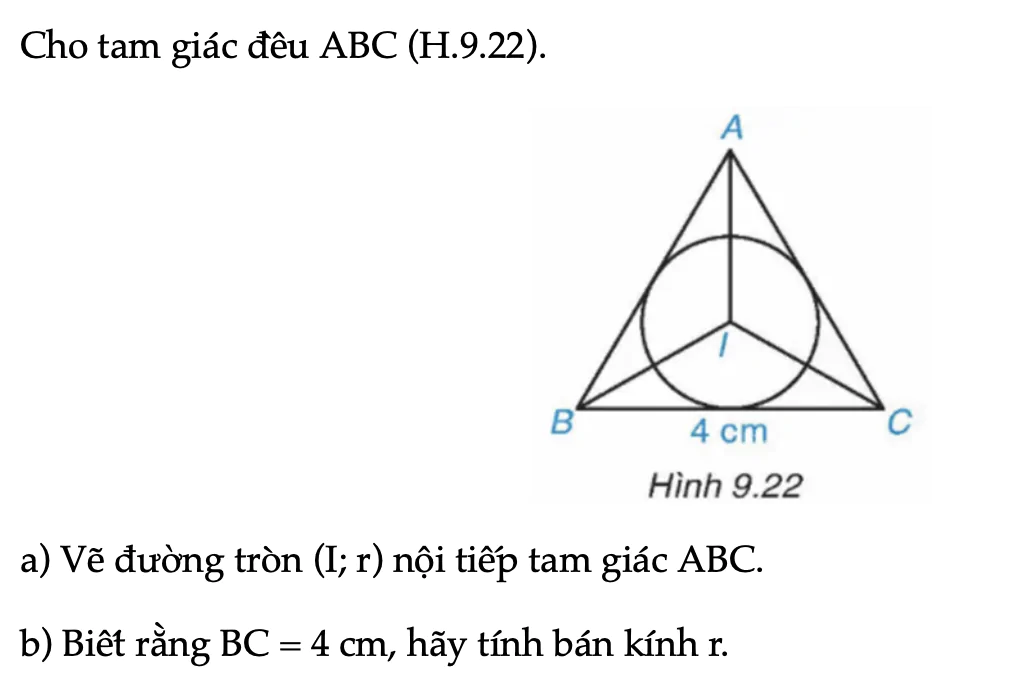
Luyện tập 3 trang 76 Toán 9 Tập 2
Cho tam giác đều ABC (H.9.22). a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC. b) Biết rằng BC = 4 cm, hãy tính bán kính r.

Bài 9.7 trang 76 Toán 9 Tập 2
Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng 2√2 cm.
Bài 9.8 trang 76 Toán 9 Tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3 cm. Tính diện tích tam giác ABC.

Bài 9.9 trang 76 Toán 9 Tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng góc BAH=OAC.
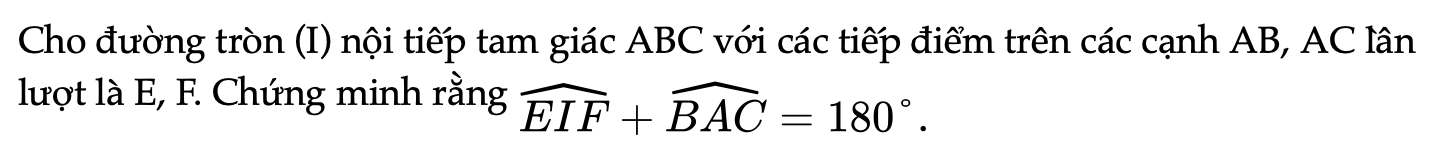
Bài 9.10 trang 76 Toán 9 Tập 2
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng góc EIF+BAC=180°.

Bài 9.11 trang 76 Toán 9 Tập 2
Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1 cm.

Bài 9.12 trang 76 Toán 9 Tập 2
Người ta muốn làm một khung gỗ hình tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30 cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?
Giải bài tập Luyện tập chung trang 78

Bài 9.13 trang 79 Toán 9 Tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng BOC=120° và OCA=20°. Tính số đo các góc của tam giác ABC.

Bài 9.14 trang 79 Toán 9 Tập 2
Cho ABC là tam giác đều có cạnh bằng 4 cm. Tính bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC.
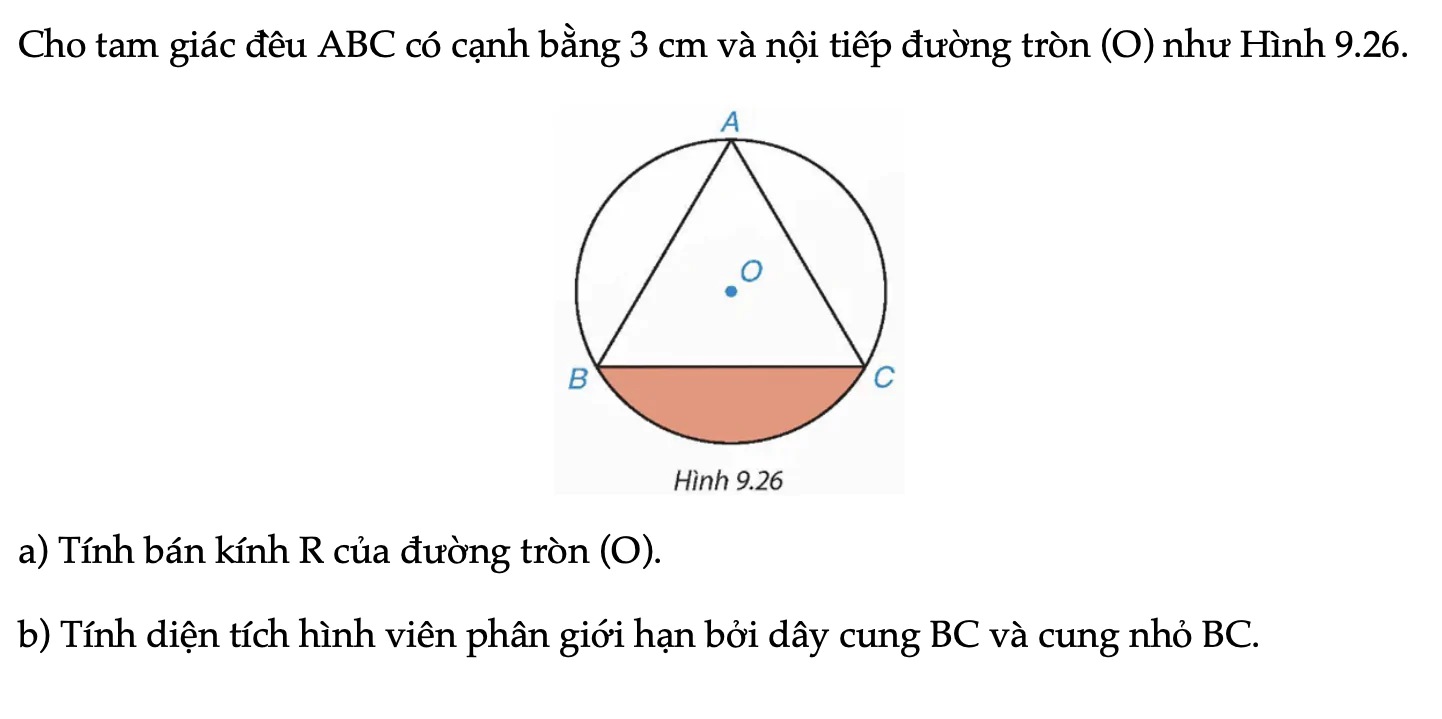
Bài 9.15 trang 79 Toán 9 Tập 2
Cho tam giác đều ABC có cạnh bằng 3 cm và nội tiếp đường tròn (O) như Hình 9.26. a) Tính bán kính R của đường tròn (O). b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.

Bài 9.16 trang 79 Toán 9 Tập 2
Trong một khu vui chơi có dạng hình tam giác đều với cạnh bằng 60 m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng.

Bài 9.17 trang 79 Toán 9 Tập 2
Người ta vẽ bản quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900 m, 1 200 m và 1 500 m (H.9.27).
Giải bài tập Bài 29. Tứ giác nội tiếp

Mở đầu trang 80 Toán 9 Tập 2
Với mỗi tam giác cho trước luôn có một đường tròn đi qua ba đỉnh của tam giác đó. Điều này có đúng với tứ giác hay không? Trong bài học này, các em sẽ tìm hiểu vấn đề đó.
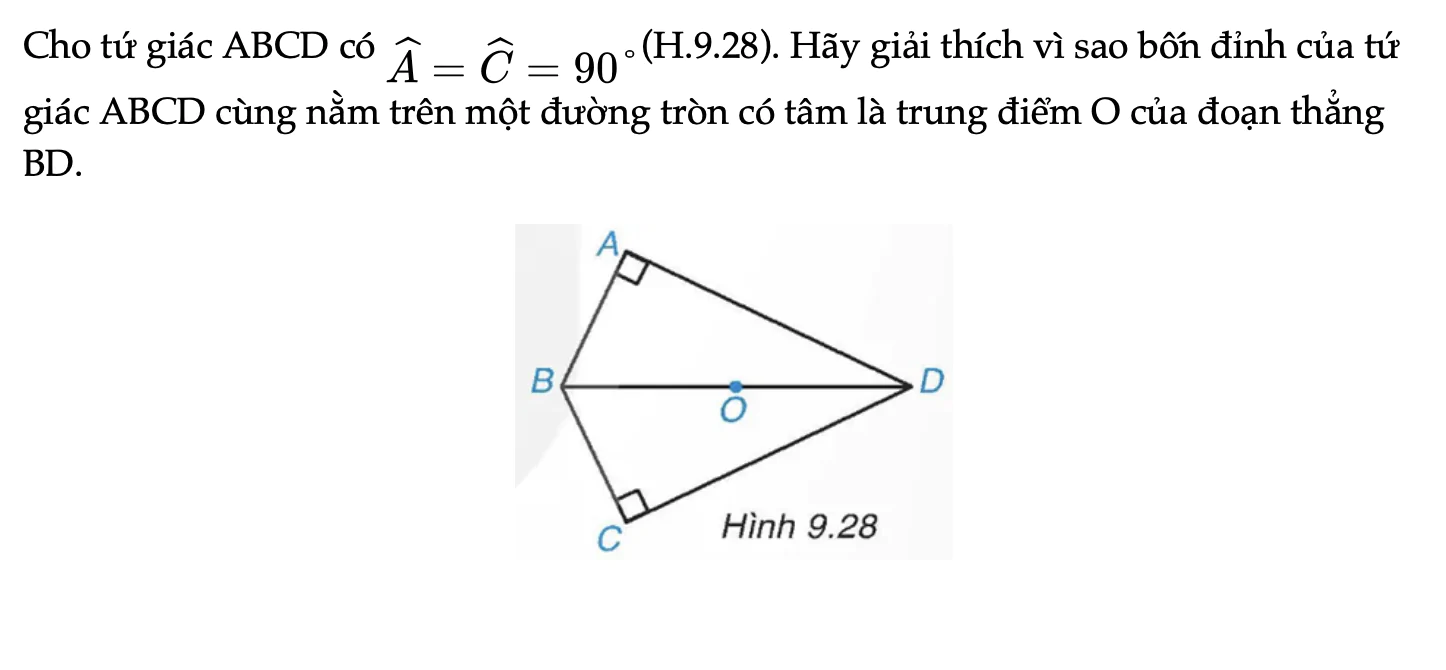
HĐ1 trang 80 Toán 9 Tập 2
Cho tứ giác ABCD có A=C=90°(H.9.28). Hãy giải thích vì sao bốn đỉnh của tứ giác ABCD cùng nằm trên một đường tròn có tâm là trung điểm O của đoạn thẳng BD.
HĐ2 trang 80 Toán 9 Tập 2
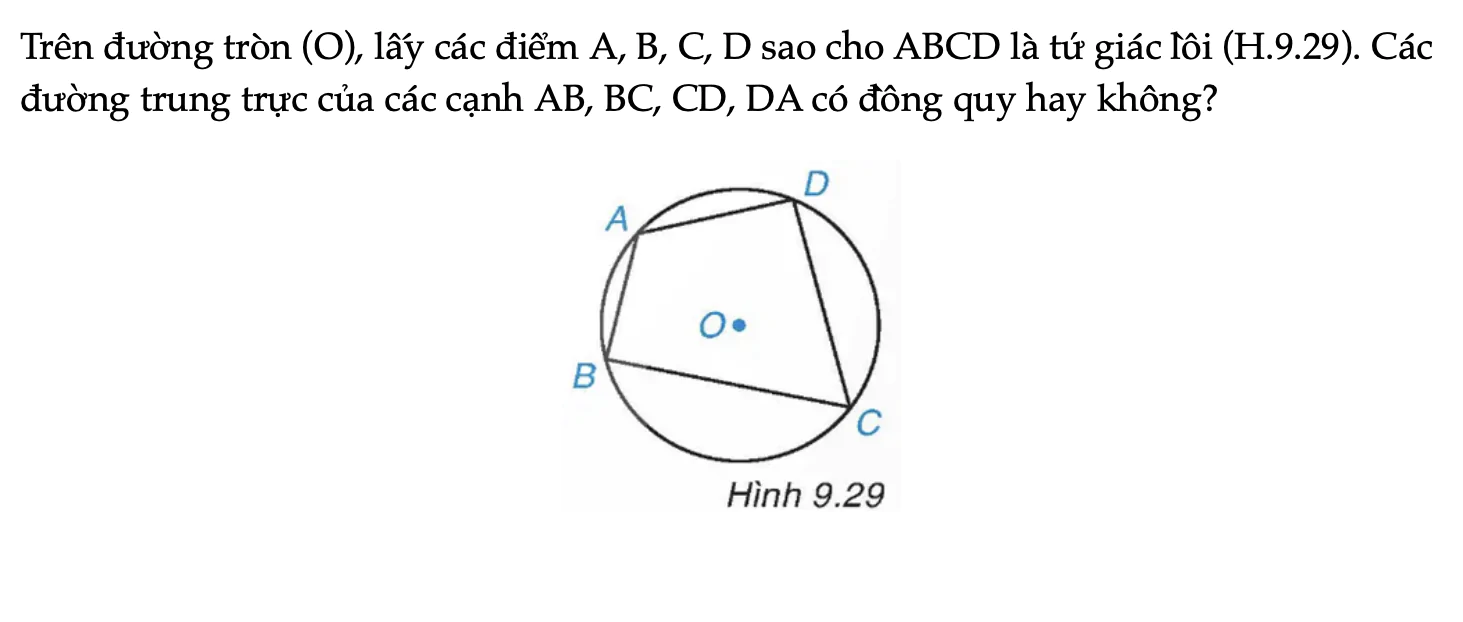
Trên đường tròn (O), lấy các điểm A, B, C, D sao cho ABCD là tứ giác lồi (H.9.29). Các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy hay không?
HĐ3 trang 81 Toán 9 Tập 2
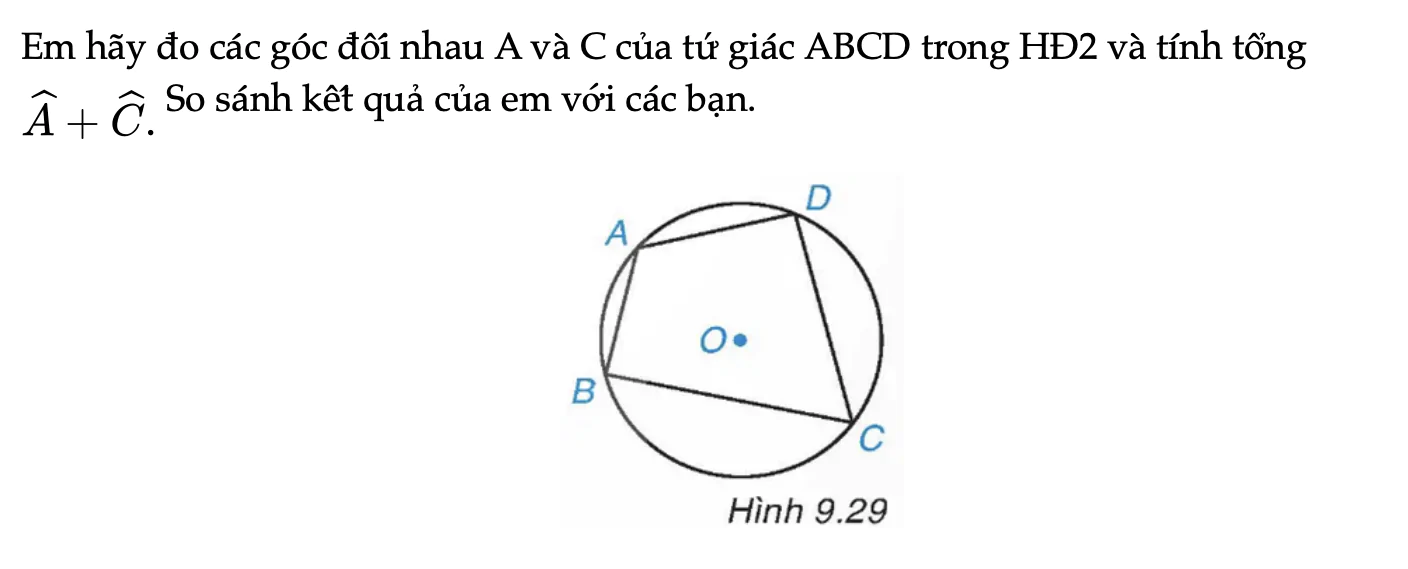
Em hãy đo các góc đối nhau A và C của tứ giác ABCD trong HĐ2 và tính tổng A+C. So sánh kết quả của em với các bạn.

Luyện tập 1 trang 81 Toán 9 Tập 2
Cho tam giác ABC có các đường cao BE, CF. Biết rằng B=60°, C=80°. a) Chứng tỏ rằng tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC. b) Tính số đo của các góc BFE và CEF.

Thử thách nhỏ 1 trang 82 Toán 9 Tập 2
Cho tứ giác ABCD, biết rằng các đường trung trực của ba đoạn thẳng AB, AC, AD đồng quy tại một điểm. Hãy giải thích vì sao ABCD là tứ giác nội tiếp.
HĐ4 trang 82 Toán 9 Tập 2
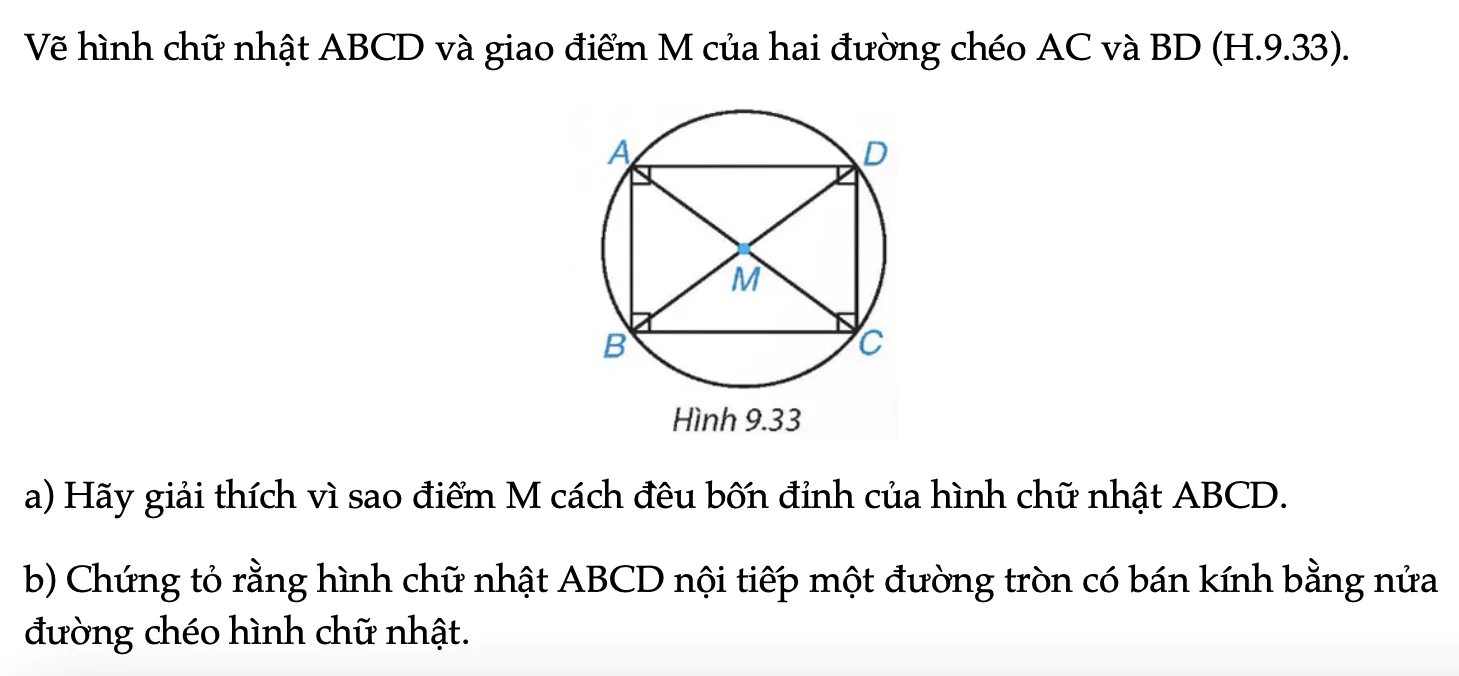
Vẽ hình chữ nhật ABCD và giao điểm M của hai đường chéo AC và BD (H.9.33). a) Hãy giải thích vì sao điểm M cách đều bốn đỉnh của hình chữ nhật ABCD b) Chứng tỏ rằng hình chữ nhật ABCD nội tiếp một đường tròn có bán kính bằng nửa đường chéo hình chữ nhật
HĐ5 trang 82 Toán 9 Tập 2
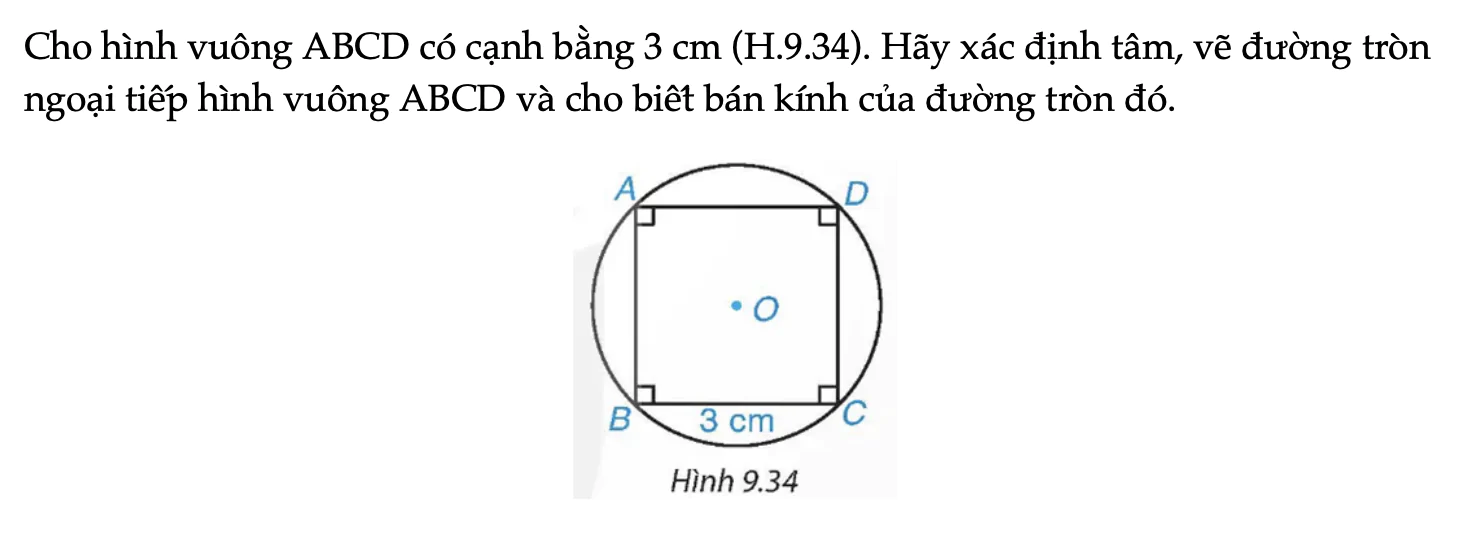
Cho hình vuông ABCD có cạnh bằng 3 cm (H.9.34). Hãy xác định tâm, vẽ đường tròn ngoại tiếp hình vuông ABCD và cho biết bán kính của đường tròn đó.

Câu hỏi trang 82 Toán 9 Tập 2
Với điểm A cho trước nằm trên đường tròn (O), có bao nhiêu hình vuông có một đỉnh là A nội tiếp đường tròn (O)?

Luyện tập 2 trang 83 Toán 9 Tập 2
Cho hình thoi ABCD có các cạnh bằng 3 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng tỏ rằng tứ giác MNPQ là hình chữ nhật và tìm bán kính đường tròn ngoại tiếp của tứ giác đó.
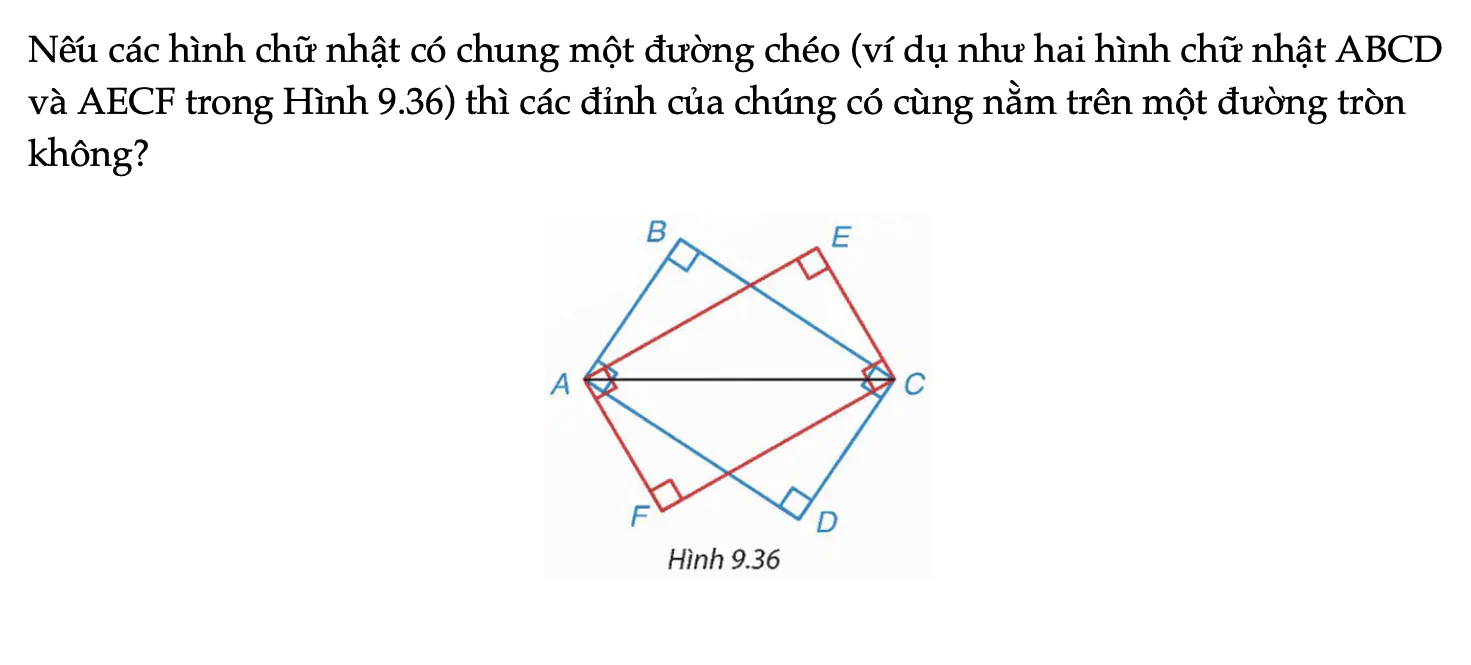
Thử thách nhỏ 2 trang 83 Toán 9 Tập 2
Nếu các hình chữ nhật có chung một đường chéo (ví dụ như hai hình chữ nhật ABCD và AECF trong Hình 9.36) thì các đỉnh của chúng có cùng nằm trên một đường tròn không?

Bài 9.18 trang 83 Toán 9 Tập 2
Cho ABCD là tứ giác nội tiếp. Tính số đo của các góc còn lại của tứ giác trong mỗi trường hợp sau.

Bài 9.19 trang 83 Toán 9 Tập 2
Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại bốn điểm A, B và C, D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng.

Bài 9.20 trang 83 Toán 9 Tập 2
Cho hình bình hành ABCD nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình chữ nhật.

Bài 9.21 trang 83 Toán 9 Tập 2
Cho hình thang ABCD (AB song song với CD) nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình thang cân.

Bài 9.22 trang 83 Toán 9 Tập 2
Tính diện tích của một hình chữ nhật, biết rằng hình chữ nhật đó có chiều dài gấp hai lần chiều rộng và bán kính đường tròn ngoại tiếp bằng 2,5 cm.
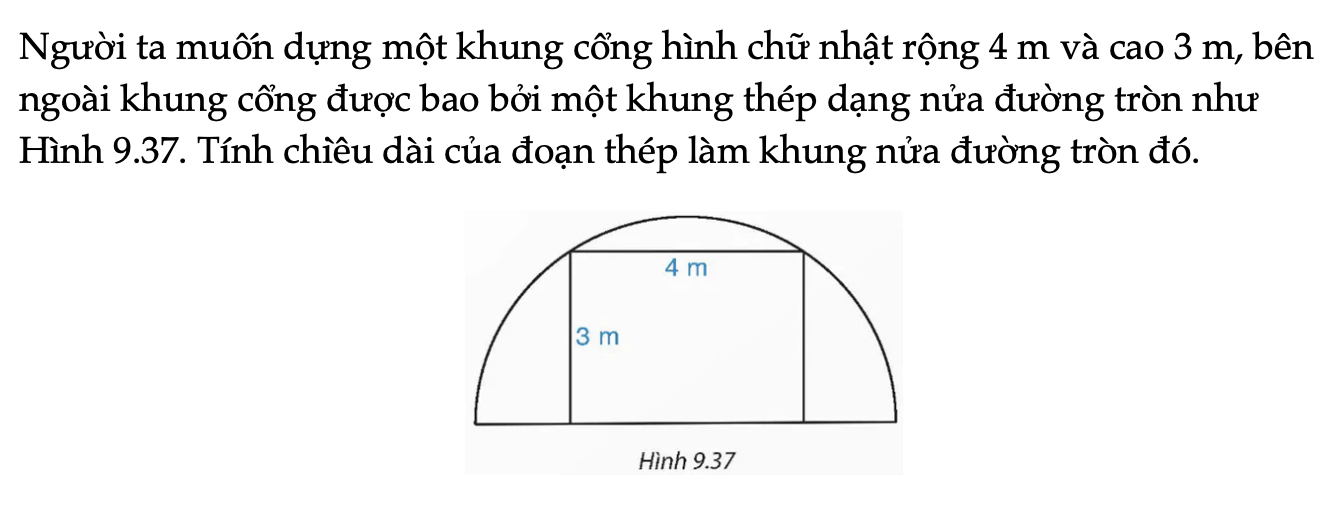
Bài 9.23 trang 83 Toán 9 Tập 2
Người ta muốn dựng một khung cổng hình chữ nhật rộng 4 m và cao 3 m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa đường tròn như Hình 9.37. Tính chiều dài của đoạn thép làm khung nửa đường tròn đó.
Giải bài tập Bài 30. Đa giác đều

HĐ1 trang 84 Toán 9 Tập 2
Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau.
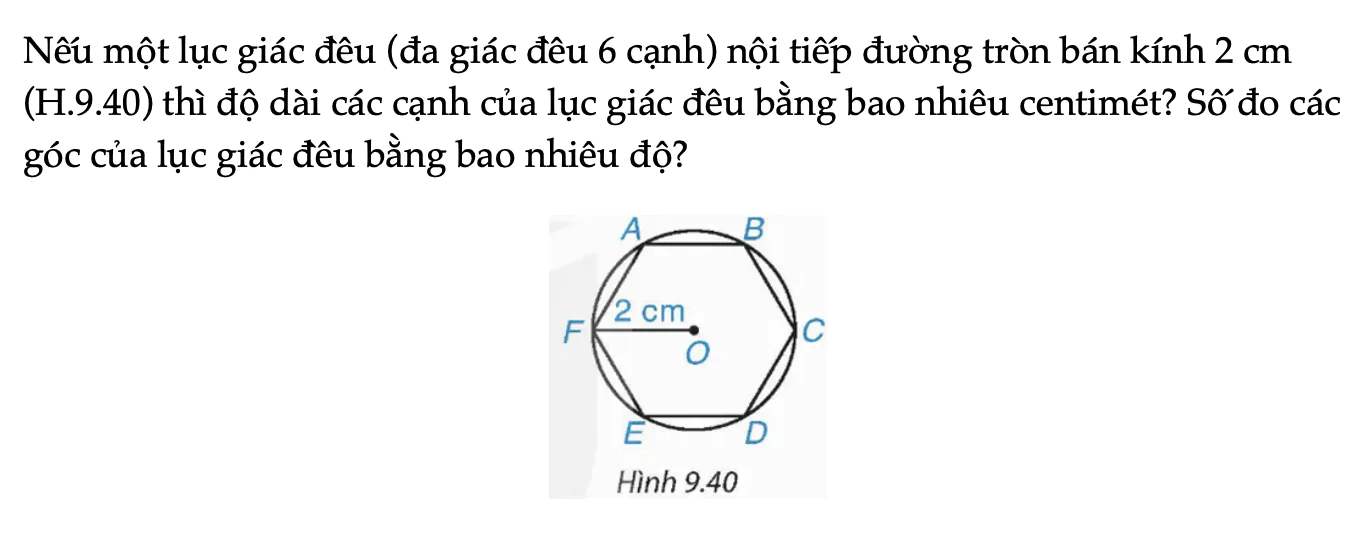
Câu hỏi trang 85 Toán 9 Tập 2
Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp đường tròn bán kính 2 cm (H.9.40) thì độ dài các cạnh của lục giác đều bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?
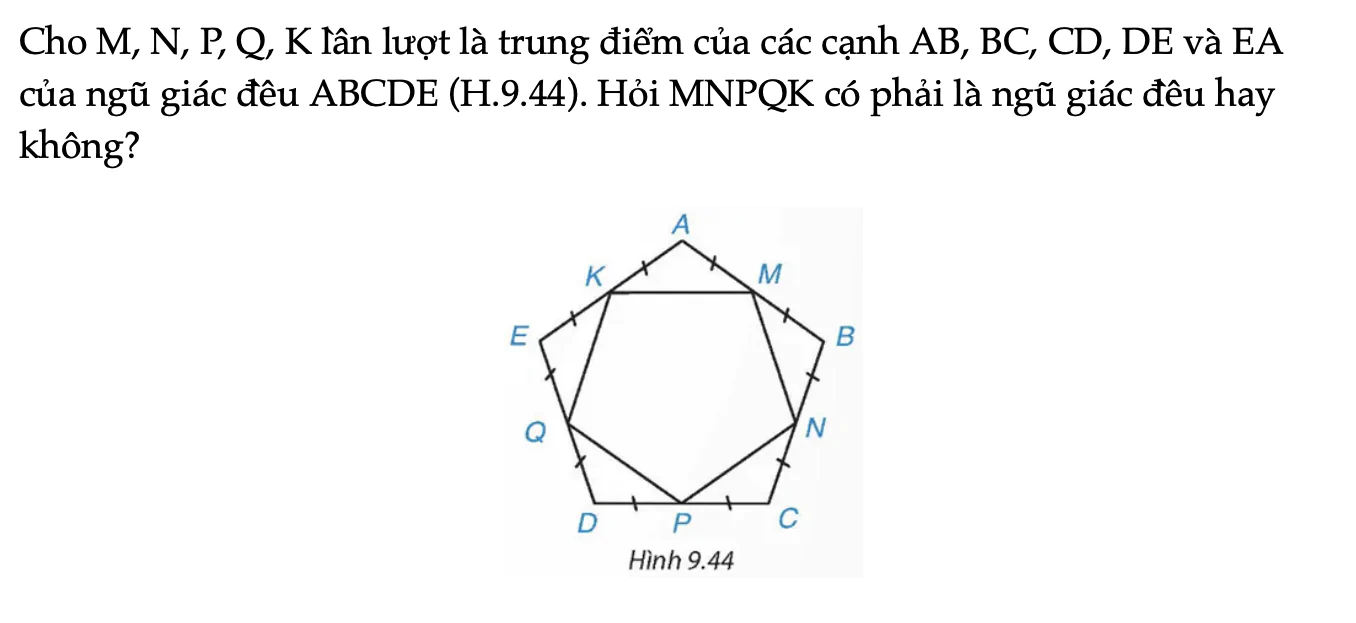
Luyện tập 1 trang 86 Toán 9 Tập 2
Cho M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA của ngũ giác đều ABCDE (H.9.44). Hỏi MNPQK có phải là ngũ giác đều hay không?
Thử thách nhỏ 1 trang 87 Toán 9 Tập 2
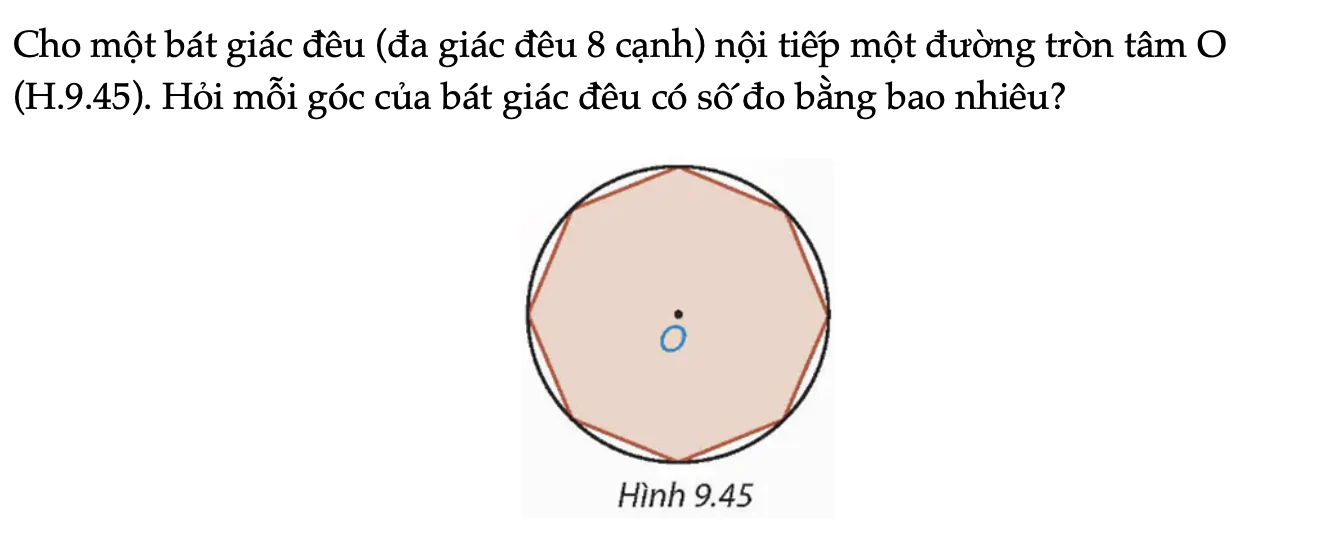
Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?

HĐ2 trang 87 Toán 9 Tập 2
Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có dạng hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay có dạng hình tròn với tâm O sao cho điểm A khác điểm O.
HĐ3 trang 87 Toán 9 Tập 2
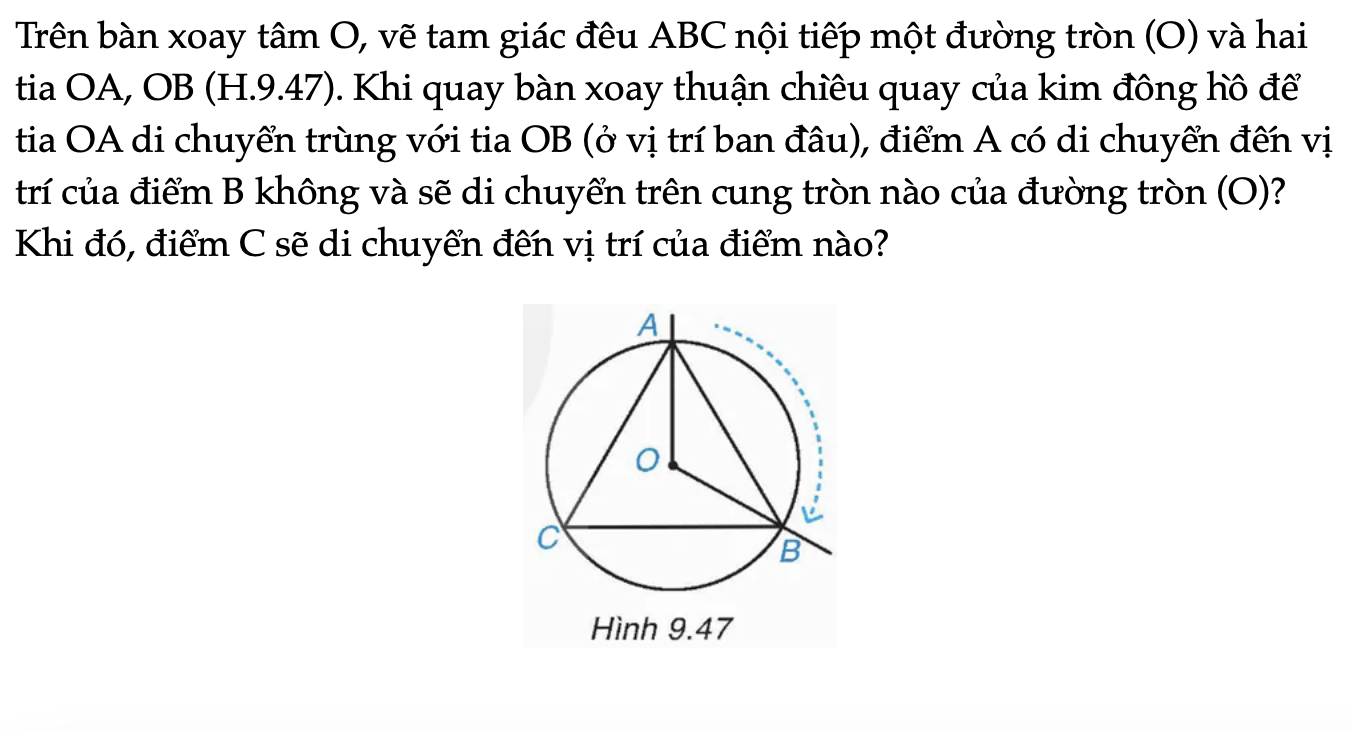
Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) và hai tia OA, OB (H.9.47).

Câu hỏi trang 88 Toán 9 Tập 2:
a) Phép quay ngược chiều 180° tâm O biến điểm A thành điểm A’. Hỏi điểm A’ có đối xứng với điểm A qua O hay không? b) Nếu phép quay thuận chiều α° tâm O biến điểm A thành điểm B thì phép quay ngược chiều α° tâm O có biến điểm B thành điểm A hay không?
Luyện tập 2 trang 88 Toán 9 Tập 2
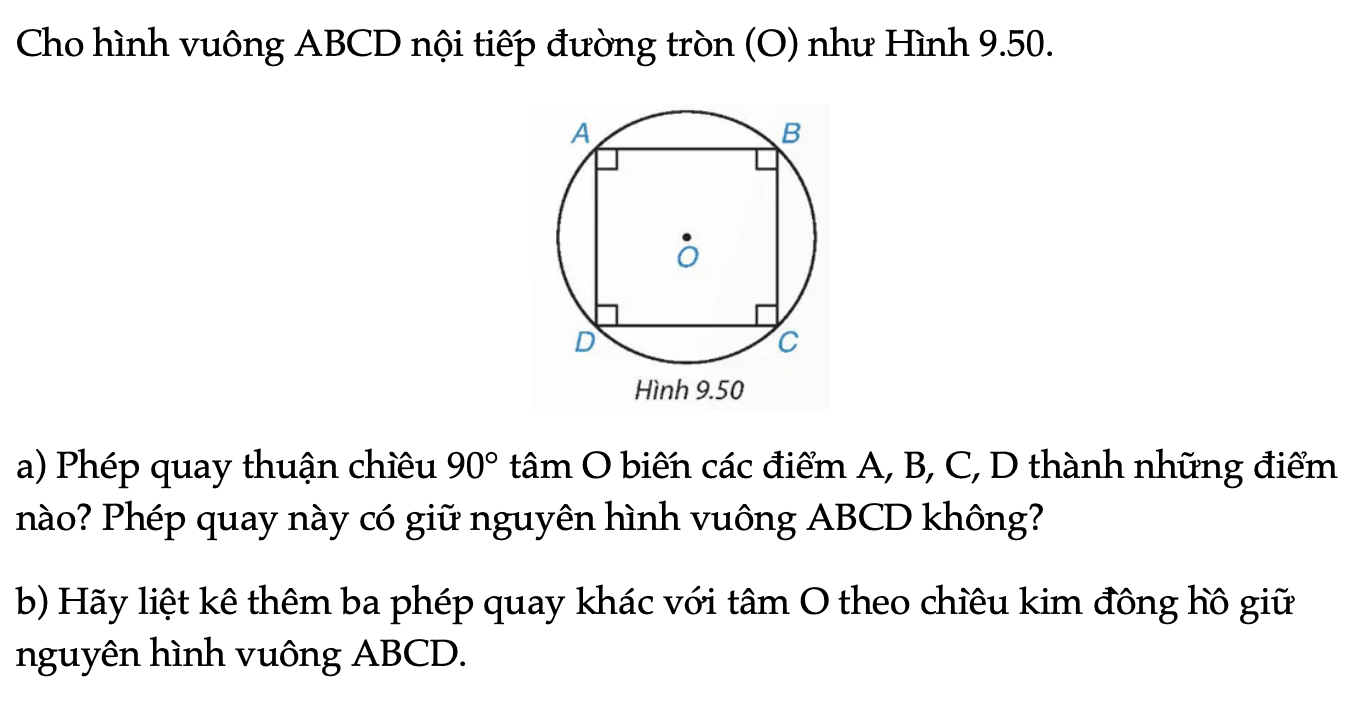
Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.50.
Thực hành trang 88 Toán 9 Tập 2
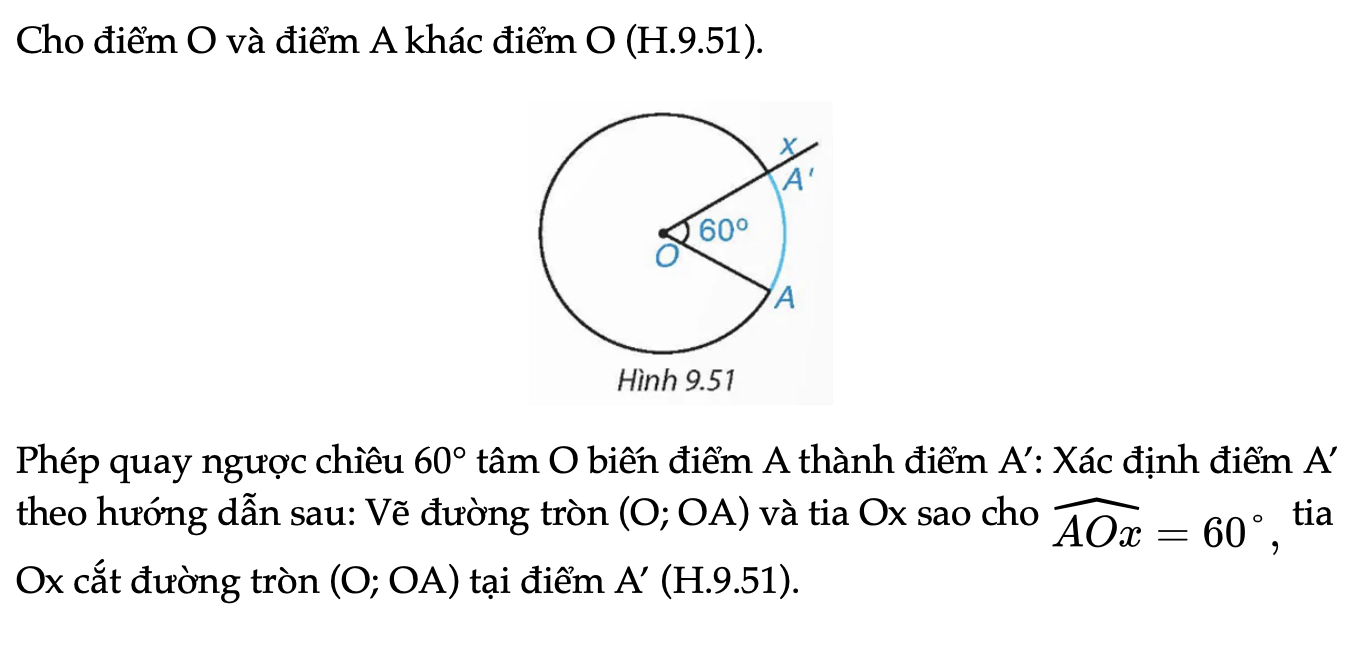
Cho điểm O và điểm A khác điểm O (H.9.51). Phép quay ngược chiều 60° tâm O biến điểm A thành điểm A’: Xác định điểm A’ theo hướng dẫn sau: Vẽ đường tròn (O; OA) và tia Ox sao cho ˆAOx=60°, tia Ox cắt đường tròn (O; OA) tại điểm A’ (H.9.51).
Thử thách nhỏ 2 trang 89 Toán 9 Tập 2
Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O).
Bài 9.24 trang 89 Toán 9 Tập 2
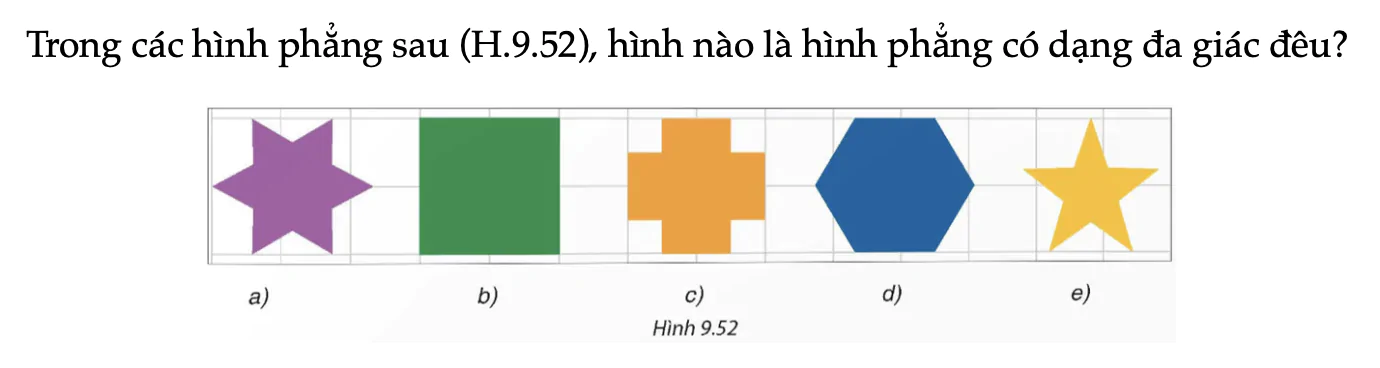
Trong các hình phẳng sau (H.9.52), hình nào là hình phẳng có dạng đa giác đều?
Bài 9.25 trang 89 Toán 9 Tập 2
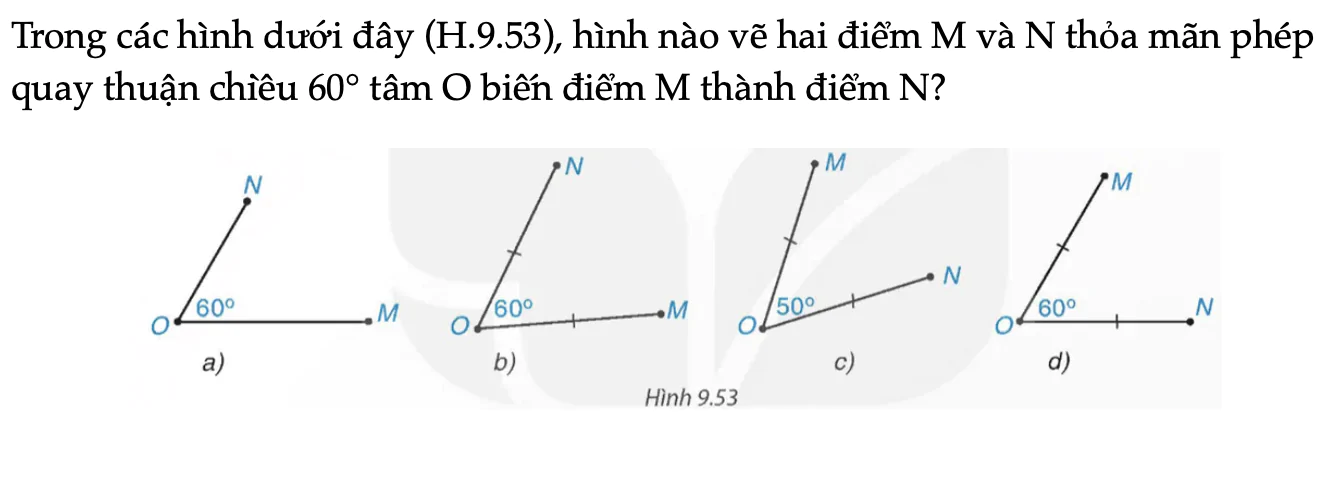
Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều 60° tâm O biến điểm M thành điểm N?

Bài 9.26 trang 89 Toán 9 Tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm. Tính độ dài các cạnh của tam giác ABC.

Bài 9.27 trang 89 Toán 9 Tập 2
Cho hình thoi ABCD có ˆA=60°. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Bài 9.28 trang 89 Toán 9 Tập 2
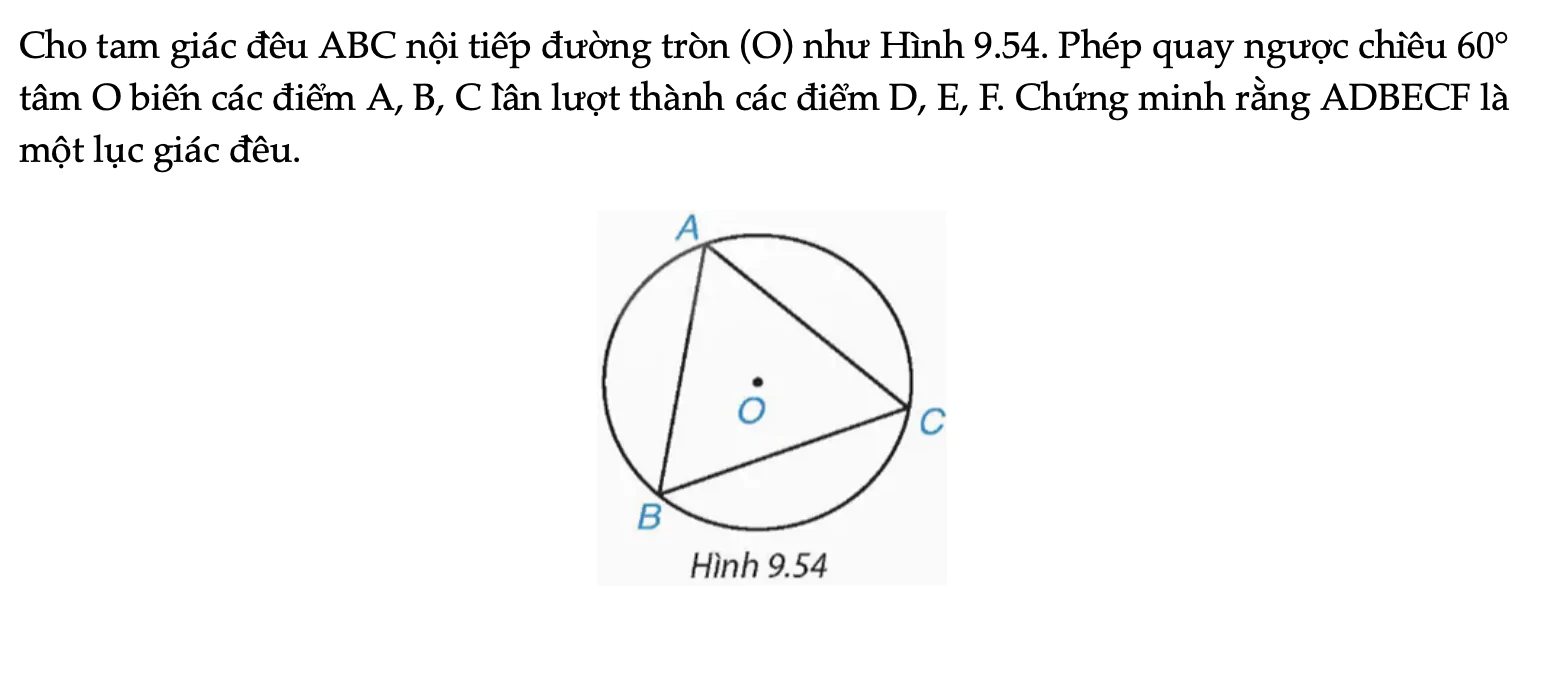
Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.54. Phép quay ngược chiều 60° tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.

Bài 9.29 trang 89 Toán 9 Tập 2
Liệt kê năm phép quay giữ nguyên một ngũ giác đều nội tiếp một đường tròn tâm O.
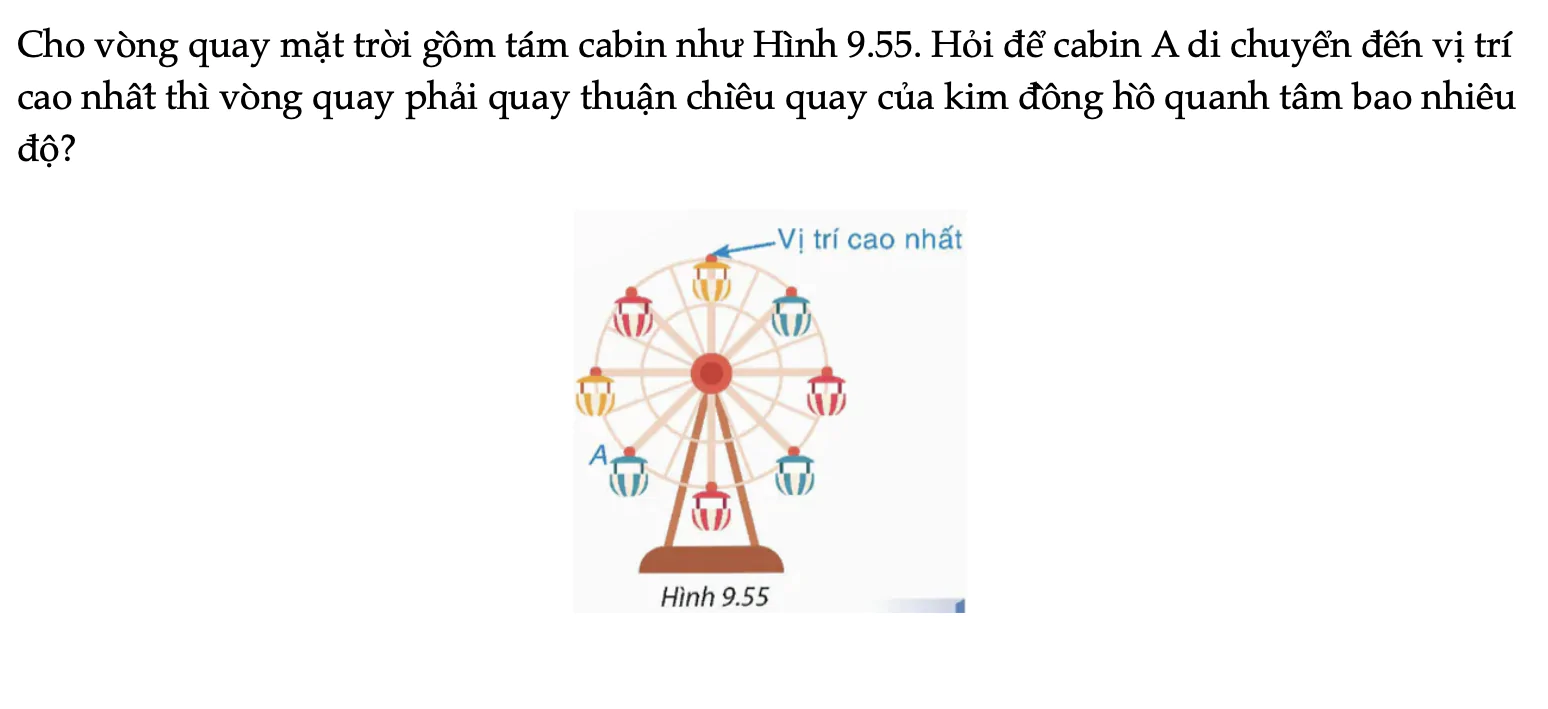
Bài 9.30 trang 89 Toán 9 Tập 2
Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều quay của kim đồng hồ quanh tâm bao nhiêu độ?
Giải bài tập Luyện tập chung trang 90
Bài 9.31 trang 91 Toán 9 Tập 2
Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.
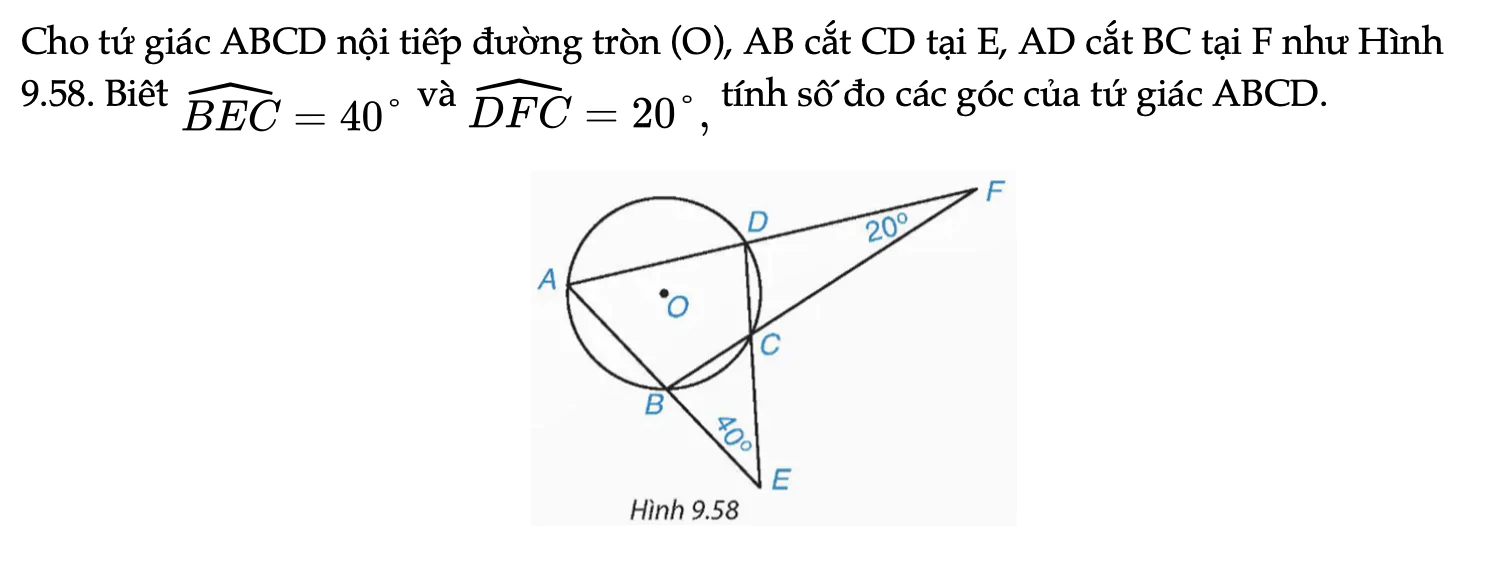
Bài 9.32 trang 91 Toán 9 Tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. BiếtˆBEC=40° và ˆDFC=20°, tính số đo các góc của tứ giác ABCD.

Bài 9.33 trang 91 Toán 9 Tập 2
Cho hình vuông ABCD có cạnh bằng 4 cm. Tính chu vi, diện tích của các đường tròn nội tiếp và ngoại tiếp hình vuông ABCD.

Bài 9.34 trang 91 Toán 9 Tập 2
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều quay của kim đồng hồ. Phép quay thuận chiều 45° biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.
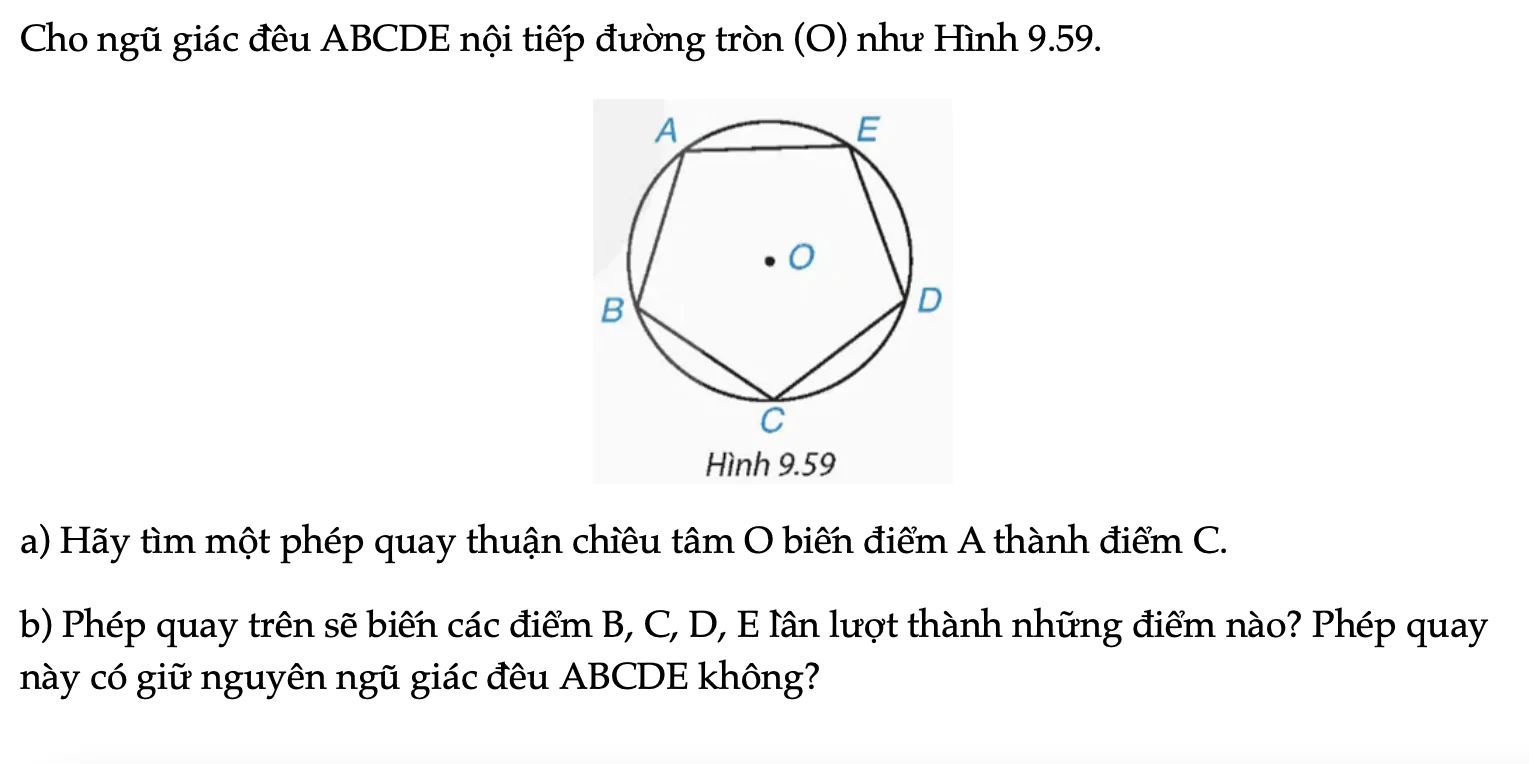
Bài 9.35 trang 91 Toán 9 Tập 2
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như Hình 9.59. a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C. b) Phép quay trên sẽ biến các điểm B, C, D, E lần lượt thành những điểm nào?

Bài 9.36 trang 91 Toán 9 Tập 2
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có S bằng 2 lần S mỗi hình thang?
Giải bài tập Bài tập cuối chương 9

Bài 9.37 trang 92 Toán 9 Tập 2
Khẳng định nào sau đây là đúng?

Bài 9.38 trang 92 Toán 9 Tập 2
Cho tứ giác ABCD nội tiếp một đường tròn có ˆA−ˆC=100°. Khẳng định nào dưới đây là đúng?

Bài 9.39 trang 92 Toán 9 Tập 2
Đa giác nào dưới đây không nội tiếp một đường tròn?

Bài 9.40 trang 92 Toán 9 Tập 2
Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng.

Bài 9.41 trang 92 Toán 9 Tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.

Bài 9.42 trang 92 Toán 9 Tập 2
Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3 cm. Tính chu vi và diện tích của một hình lục giác đều đã cho.
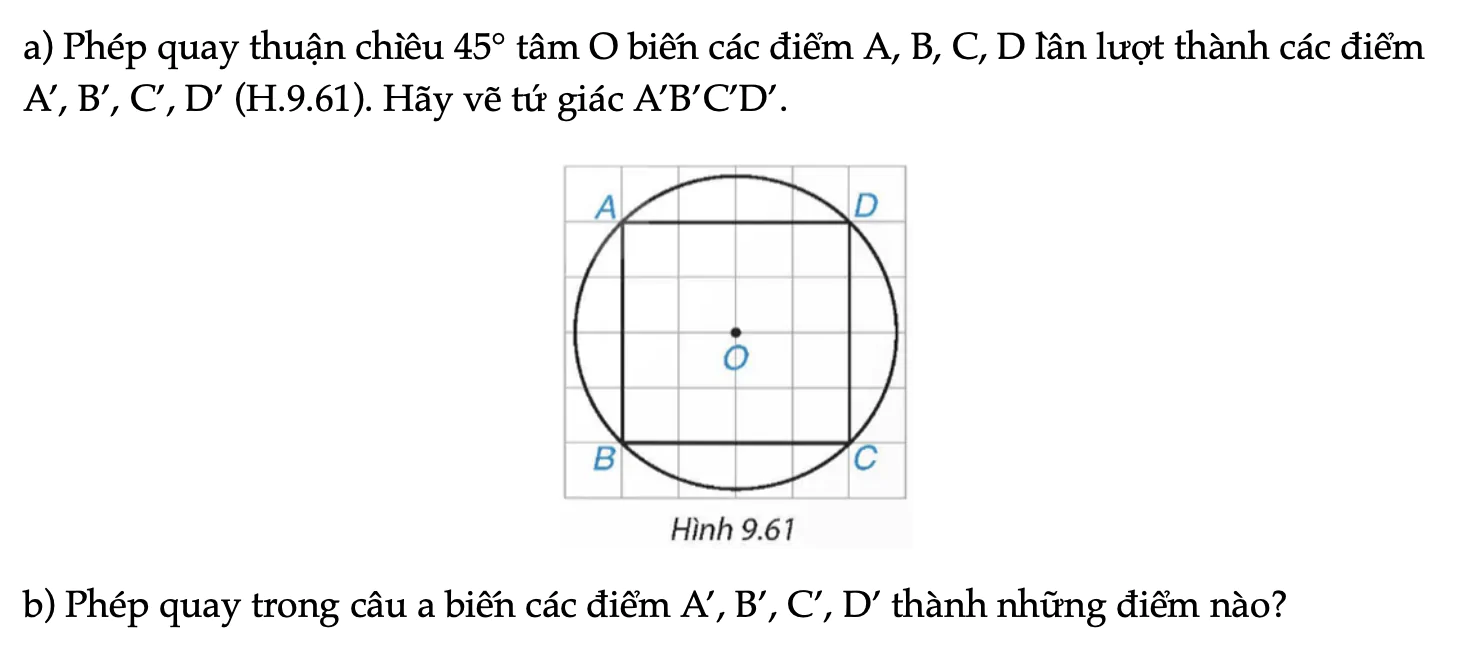
Bài 9.43 trang 92 Toán 9 Tập 2
a) Phép quay thuận chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ (H.9.61). Hãy vẽ tứ giác A’B’C’D’. b) Phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm nào?
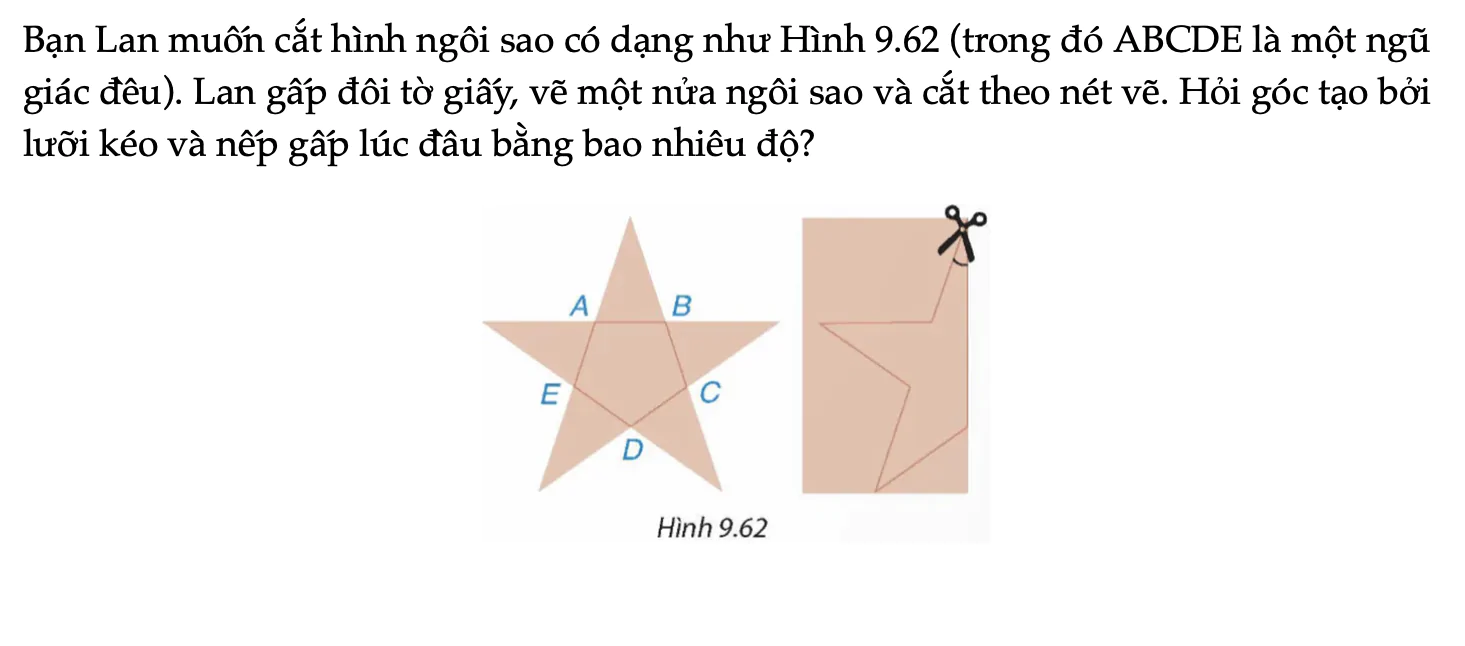
Bài 9.44 trang 92 Toán 9 Tập 2
Bạn Lan muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Hỏi góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu độ?