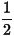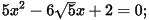Giải bài tập Toán 9 Bài tập cuối chương 6 | Kết Nối Tri Thức
Hướng dẫn giải chi tiết Bài tập cuối chương 6
Bài 6.39 trang 30 Toán 9 Tập 2
Điểm nào sau đây thuộc đồ thị của hàm số 
A. (1; 2).
B. (2; 1).
C. (–1; 2).
D.
Bài 6.40 trang 30 Toán 9 Tập 2
Hình 6.11 là hai đường parabol trong mặt phẳng toạ độ Oxy. Khẳng định nào sau đây là đúng?
A. a < 0 < b.
B. a < b < 0.
C. a > b > 0.
D. a > 0 > b.
Bài 6.41 trang 30 Toán 9 Tập 2
Các nghiệm của phương trình x2 + 7x + 12 = 0 là
A. x1 = 3; x2 = 4.
B. x1 = –3; x2 = –4.
C. x1 = 3; x2 = –4.
D. x1 = –3; x2 = 4.
Bài 6.42 trang 30 Toán 9 Tập 2
Phương trình bậc hai có hai nghiệm x1 = 13 và x2 = 25 là
A. x2 – 13x + 25 = 0.
B. x2 – 25x + 13 = 0.
C. x2 – 38x + 325 = 0.
D. x2 + 38x + 325 = 0.
Bài 6.43 trang 30 Toán 9 Tập 2
Gọi x1, x2 là hai nghiệm của phương trình x2 – 5x + 6 = 0. Khi đó, giá trị của biểu thức 
là
A. 13.
B. 19.
C. 25.
D. 5.
Bài 6.44 trang 30 Toán 9 Tập 2
Chiều dài và chiều rộng của hình chữ nhật có chu vi 20 cm và diện tích 24 cm2 là
A. 5 cm và 4 cm.
B. 6 cm và 4 cm.
C. 8 cm và 3 cm.
D. 10 cm và 2 cm.
Bài 6.45 trang 30 Toán 9 Tập 2
Vẽ đồ thị của các hàm số 
và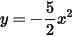 
trên cùng một mặt phẳng toạ độ.
Bài 6.46 trang 30 Toán 9 Tập 2
Cho hàm số y = ax2. Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(3; 3). Vẽ đồ thị của hàm số trong trường hợp đó.
Bài 6.48 trang 31 Toán 9 Tập 2
Cho phương trình x2 – 11x + 30 = 0. Gọi x1, x2 là hai nghiệm của phương trình. Không giải phương trình, hãy tính:
a) 
b) 
Bài 6.49 trang 31 Toán 9 Tập 2
Tìm hai số u và v, biết:
a) u + v = 13 và uv = 40;
b) u – v = 4 và uv = 77.
Bài 6.50 trang 31 Toán 9 Tập 2
Các kĩ sư đảm bảo an toàn của đường cao tốc thường sử dụng công thức d = 0,05v2 + 1,1v để ước tính khoảng cách an toàn tối thiểu d (feet) (tức là độ dài quãng đường mà xe đi được kể từ khi đạp phanh đến khi xe dừng lại) đối với một phương tiện di chuyển với tốc độ v (dặm/giờ) (theo Algebra 2, NXB McGraw-Hill, 2008). Giả sử giới hạn tốc độ trên một đường cao tốc nào đó là 70 dặm/giờ. Nếu một ô tô có thể dừng lại sau 300 feet kể từ khi đạp phanh thì ô tô đó có chạy nhanh hơn giới hạn tốc độ của đường cao tốc này không?
Bài 6.51 trang 31 Toán 9 Tập 2
Bác Hương gửi tiết kiệm ngân hàng 100 triệu đồng với kì hạn 12 tháng. Sau một năm, do chưa có nhu cầu sử dụng nên bác chưa rút sổ tiết kiệm này ra mà gửi tiếp và gửi thêm một sổ tiết kiệm mới với số tiền 50 triệu đồng, cũng với kì hạn 12 tháng. Sau hai năm (kể từ khi gửi lần đầu), bác Hương nhận được số tiền cả vốn lẫn lãi là 176 triệu đồng. Tính lãi suất năm của hình thức gửi tiết kiệm này (giả sử lãi suất không đổi trong suốt quá trình gửi).
Bài 6.52 trang 31 Toán 9 Tập 2
Hai khối học sinh lớp 8 và lớp 9 của một trường trung học cơ sở tham gia lao động. Nếu làm chung thì sẽ hoàn thành công việc sau 1 giờ 12 phút. Nếu mỗi khối lớp làm riêng thì khối lớp 9 làm xong nhanh hơn khối lớp 8 là 1 giờ. Hỏi nếu mỗi khối lớp làm riêng thì sau bao lâu sẽ hoàn thành công việc?