Giải bài tập Luyện tập 1 trang 81 Toán 9 Tập 2 | Toán 9 - Kết nối tri thức

Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 1 trang 81 Toán 9 Tập 2. Bài 29. Tứ giác nội tiếp. Toán 9 - Kết nối tri thức

Đề bài:

Cho tam giác ABC có các đường cao BE, CF. Biết rằng $\hat{B} = 60 °,$ $\hat{B} = 60 °, \hat{C} = 80 ° .$ $\hat{C} = 80 ° .$

a) Chứng tỏ rằng tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC.

b) Tính số đo của các góc BFE và CEF.

Đáp án và cách giải chi tiết:

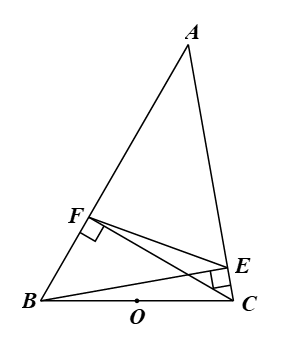
a) Vì BE, CF là hai đường cao của tam giác ABC nên BE ⊥ AC và CF ⊥ AB.

Xét ∆BCE vuông tại E, đường tròn ngoại tiếp tam giác có tâm là trung điểm O của BC và bán kính bằng nửa BC hay ba điểm B, C, E cùng nằm trên đường tròn tâm O, đường kính BC.

Xét ∆BCF vuông tại F, đường tròn ngoại tiếp tam giác có tâm là trung điểm O của BC và bán kính bằng nửa BC hay ba điểm B, C, F cùng nằm trên đường tròn tâm O, đường kính BC.

Do đó bốn điểm B, C, E, F cùng nằm trên đường tròn tâm O, đường kính BC.

Vậy tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC.

b) Vì tứ giác BCEF nội tiếp một đường tròn nên các góc đối diện có tổng số đo bằng 180°. Do đó:

$\hat{B F E} + \hat{B C E} = 180 °,$ suy ra $\hat{B F E} = 180 ° - \hat{B C E} = 180 ° - 80 ° = 100 °;$
$\hat{C E F} + \hat{C B F} = 180 °,$ suy ra $\hat{C E F} = 180 ° - \hat{C B F} = 180 ° - 60 ° = 120 ° .$

Vậy $\hat{B F E} = 100 °; \hat{C E F} = 120 ° .$

Nguồn: loigiaitoan.com

Tổng số đánh giá:

Xếp hạng: / 5 sao

Bài tập liên quan:

Mở đầu trang 80 Toán 9 Tập 2

Với mỗi tam giác cho trước luôn có một đường tròn đi qua ba đỉnh của tam giác đó. Điều này có đúng với tứ giác hay không? Trong bài học này, các em sẽ tìm hiểu vấn đề đó.

Xem cách giải chi tiết

HĐ1 trang 80 Toán 9 Tập 2

Cho tứ giác ABCD có $\hat{A} = \hat{C} = 90 °$ (H.9.28). Hãy giải thích vì sao bốn đỉnh của tứ giác ABCD cùng nằm trên một đường tròn có tâm là trung điểm O của đoạn thẳng BD.

Xem cách giải chi tiết

HĐ2 trang 80 Toán 9 Tập 2

Trên đường tròn (O), lấy các điểm A, B, C, D sao cho ABCD là tứ giác lồi (H.9.29). Các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy hay không?

Xem cách giải chi tiết

HĐ3 trang 81 Toán 9 Tập 2

Em hãy đo các góc đối nhau A và C của tứ giác ABCD trong HĐ2 và tính tổng $\hat{A} + \hat{C} .$ So sánh kết quả của em với các bạn.

Xem cách giải chi tiết

Thử thách nhỏ 1 trang 82 Toán 9 Tập 2

Cho tứ giác ABCD, biết rằng các đường trung trực của ba đoạn thẳng AB, AC, AD đồng quy tại một điểm. Hãy giải thích vì sao ABCD là tứ giác nội tiếp.

Xem cách giải chi tiết

HĐ4 trang 82 Toán 9 Tập 2

Vẽ hình chữ nhật ABCD và giao điểm M của hai đường chéo AC và BD (H.9.33).

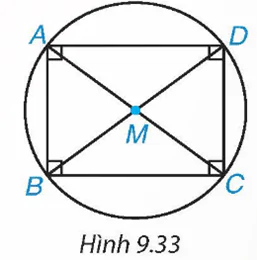
a) Hãy giải thích vì sao điểm M cách đều bốn đỉnh của hình chữ nhật ABCD.

b) Chứng tỏ rằng hình chữ nhật ABCD nội tiếp một đường tròn có bán kính bằng nửa đường chéo hình chữ nhật.

Xem cách giải chi tiết

HĐ5 trang 82 Toán 9 Tập 2

Cho hình vuông ABCD có cạnh bằng 3 cm (H.9.34). Hãy xác định tâm, vẽ đường tròn ngoại tiếp hình vuông ABCD và cho biết bán kính của đường tròn đó.

Xem cách giải chi tiết

Câu hỏi trang 82 Toán 9 Tập 2

Với điểm A cho trước nằm trên đường tròn (O), có bao nhiêu hình vuông có một đỉnh là A nội tiếp đường tròn (O)?

Xem cách giải chi tiết

Luyện tập 2 trang 83 Toán 9 Tập 2

Cho hình thoi ABCD có các cạnh bằng 3 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng tỏ rằng tứ giác MNPQ là hình chữ nhật và tìm bán kính đường tròn ngoại tiếp của tứ giác đó.

Xem cách giải chi tiết

Thử thách nhỏ 2 trang 83 Toán 9 Tập 2

Nếu các hình chữ nhật có chung một đường chéo (ví dụ như hai hình chữ nhật ABCD và AECF trong Hình 9.36) thì các đỉnh của chúng có cùng nằm trên một đường tròn không?