Giải bài tập HĐ3 trang 73 Toán 9 Tập 2 | Toán 9 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập HĐ3 trang 73 Toán 9 Tập 2. Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác. Toán 9 - Kết nối tri thức
Đề bài:
Cho tam giác ABC vuông tại đỉnh A (H.9.15). Gọi N, P lần lượt là trung điểm của các cạnh AB và AC.
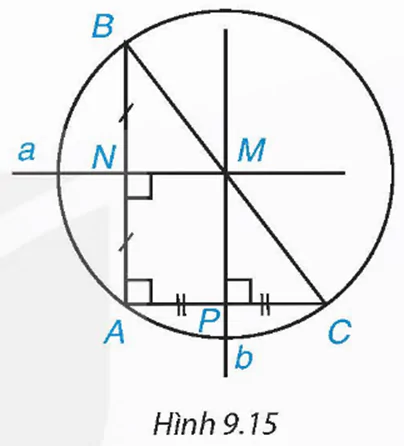
a) Vẽ hai đường trung trực a, b của các cạnh AB, AC, cắt nhau tại M.
b) Hãy giải thích vì sao MN, MP là các đường trung bình của tam giác ABC.
c) Hãy giải thích vì sao M là trung điểm của BC, từ đó suy ra đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính
Đáp án và cách giải chi tiết:
a) Vẽ đường thẳng a vuông góc với AB tại N và vẽ đường thẳng b vuông góc với AC tại P, ta được hai đường trung trực a, b của các cạnh AB, AC. Hai đường thẳng a và b cắt nhau tại M.
b) Vì ∆ABC vuông tại A nên AB ⊥ AC. (1)
Vì a là đường trung trực của AB nên a ⊥ AB hay MN ⊥ AB. (2)
Vì b là đường trung trực của AC nên b ⊥ AC hay MP ⊥ AC. (3)
Từ (1) và (2) suy ra MN // AC.
Từ (1) và (3) suy ra MP // AB.
Xét ∆ABC có:
⦁ N là trung điểm của AB và MN // AC nên MN là đường trung bình của tam giác.
⦁ P là trung điểm của AC và MP // AB nên MP là đường trung bình của tam giác.
c) Vì MN là đường trung bình của tam giác ABC nên M là trung điểm của BC.
Suy ra
Lại có M thuộc đường trung trực của AB nên MA = MB.
Do đó
Vậy đường tròn ngoại tiếp của tam giác ABC có tâm M là bán kính
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Mở đầu trang 72 Toán 9 Tập 2:
Cho trước một tam giác ABC. Bằng thước kẻ và compa, em có thể vẽ được một đường tròn đi qua ba đỉnh của tam giác và đường tròn tiếp xúc với cả ba cạnh của tam giác hay không?
HĐ1 trang 72 Toán 9 Tập 2
Cho d là đường trung trực của đoạn thẳng AB và O là một điểm trên d (H.9.12). Hỏi đường tròn tâm O đi qua A thì có đi qua B không?

HĐ2 trang 72 Toán 9 Tập 2
Cho tam giác ABC có ba đường trung trực đồng quy tại O (H.9.13). Hãy giải thích tại sao đường tròn (O; OA) đi qua ba đỉnh của tam giác ABC.

Câu hỏi trang 73 Toán 9 Tập 2
Hãy kể tên bốn tam giác nội tiếp đường tròn (O) trong Hình 9.14.

Luyện tập 1 trang 73 Toán 9 Tập 2
Cho tam giác ABC có AC = 3 cm, AB = 4 cm và BC = 5 cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
HĐ4 trang 73 Toán 9 Tập 2
a) Vẽ tam giác đều ABC. Hãy trình bày cách xác định tâm của đường tròn ngoại tiếp tam giác ABC và vẽ đường tròn đó.
b) Giải thích vì sao tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó (H.9.17).

c) Giải thích vì sao và (với M là trung điểm của BC).
Luyện tập 2 trang 74 Toán 9 Tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O) có bán kính bằng 4 cm. Tính độ dài các cạnh của tam giác.
HĐ5 trang 74 Toán 9 Tập 2
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).

a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.
Câu hỏi trang 75 Toán 9 Tập 2
Mỗi tam giác có bao nhiêu đường tròn nội tiếp? Có bao nhiêu tam giác cùng ngoại tiếp một đường tròn?
HĐ6 trang 75 Toán 9 Tập 2
Cho tam giác đều ABC có trọng tâm G.
a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.
b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa bán kính đường tròn ngoại tiếp tam giác ABC và bằng
Thực hành trang 75 Toán 9 Tập 2
Vẽ đường tròn nội tiếp của tam giác ABC bằng thước kẻ và compa theo các bước sau:
– Vẽ tia phân giác góc B như sau: Dùng compa vẽ một cung tròn tâm B cắt hai cạnh BC, BA lần lượt tại X và Y. Vẽ hai cung tròn tâm X, Y có cùng bán kính, hai cung này cắt nhau tại một điểm Z khác B. Kẻ tia BZ ta được tia phân giác góc B.
– Tương tự, vẽ tia phân giác góc C, cắt tia BZ tại I.
– Vẽ đường cao ID từ I xuống BC (D thuộc BC). Vẽ đường tròn (I; ID) (H.9.21).
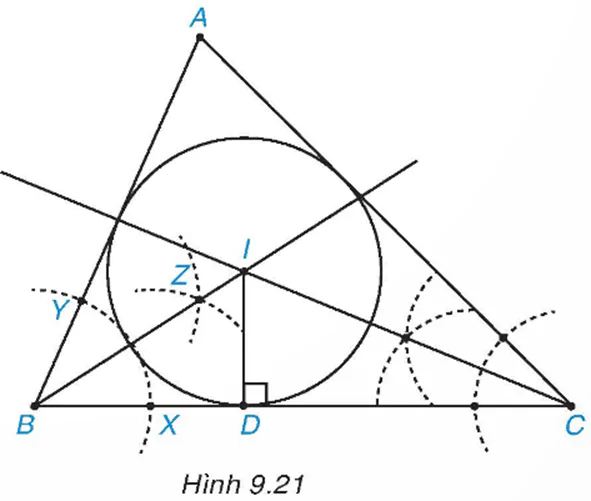
Khi đó đường tròn (I; ID) là đường tròn nội tiếp tam giác ABC cần vẽ.
Luyện tập 3 trang 76 Toán 9 Tập 2
Cho tam giác đều ABC (H.9.22).

a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.
b) Biết rằng BC = 4 cm, hãy tính bán kính r.
Bài 9.7 trang 76 Toán 9 Tập 2
Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng 2 cm.
Bài 9.8 trang 76 Toán 9 Tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3 cm. Tính diện tích tam giác ABC.
Bài 9.9 trang 76 Toán 9 Tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng
Bài 9.10 trang 76 Toán 9 Tập 2
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng
Bài 9.11 trang 76 Toán 9 Tập 2
Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1 cm.
Bài 9.12 trang 76 Toán 9 Tập 2
Người ta muốn làm một khung gỗ hình tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30 cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?
