Giải bài tập Toán 11 Chuyên đề 2. Làm quen với một vài khái niệm của lý thuyết đồ thị | Kết Nối Tri Thức
Chuyên đề 2. Làm quen với một vài khái niệm của lý thuyết đồ thị. Một số khái niệm cơ bản. Đường đi Euler và đường đi Hamilton. Bài toán tìm đường đi tối ưu trong một vài trường hợp đơn giản.
Giải bài tập Bài 8. Một số khái niệm cơ bản
Mở đầu trang 34 Chuyên đề toán 11
Mở đầu trang 34 Chuyên đề toán 11

HĐ1 trang 35 Chuyên đề Toán 11
HĐ1 trang 35 Chuyên đề Toán 11: Nhận biết khái niệm đồ thị

HĐ2 trang 36 Chuyên đề Toán 11
HĐ2 trang 36 Chuyên đề Toán 11: Nhận biết khái niệm đơn đồ thị Xét đồ thị cho trong Hình 2.2. a) Đồ thị trên có khuyên không? b) Có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh không?

HĐ3 trang 36 Chuyên đề Toán 11
HĐ3 trang 36 Chuyên đề Toán 11: Nhận biết đồ thị đầy đủ Xét đồ thị nhận được trong Luyện tập 1. Có cặp đỉnh nào của đồ thị này mà không có cạnh nào nối chúng không?
HĐ4 trang 37 Chuyên đề Toán 11
HĐ4 trang 37 Chuyên đề Toán 11: Nhận biết bậc của đỉnh Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.

HĐ5 trang 38 Chuyên đề Toán 11
HĐ5 trang 38 Chuyên đề Toán 11: Nhận biết khái niệm đường đi và chu trình

HĐ6 trang 39 Chuyên đề Toán 11
HĐ6 trang 39 Chuyên đề Toán 11: Nhận biết tính liên thông của đồ thị

Luyện tập 1 trang 36 Chuyên đề Toán 11
Luyện tập 1 trang 36 Chuyên đề Toán 11
Luyện tập 2 trang 36 Chuyên đề Toán 11
Luyện tập 2 trang 36 Chuyên đề Toán 11: Vẽ đồ thị G với các đỉnh và các cạnh như sau: V(G) = {U, W, X, Z} và E(G) = {UW, WX, WZ, XZ}. G có phải là một đơn đồ thị không?
Luyện tập 3 trang 37 Chuyên đề Toán 11
Luyện tập 3 trang 37 Chuyên đề Toán 11: Vẽ các đồ thị đầy đủ có 5 đỉnh, có 6 đỉnh.

Luyện tập 4 trang 38 Chuyên đề Toán 11
Luyện tập 4 trang 38 Chuyên đề Toán 11: Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.
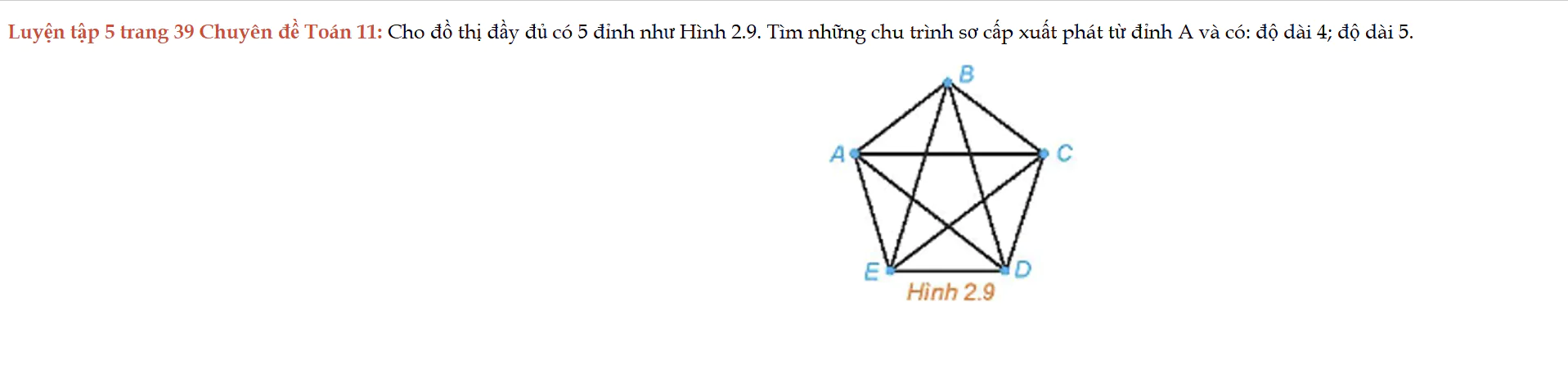
Luyện tập 5 trang 39 Chuyên đề Toán 11
Luyện tập 5 trang 39 Chuyên đề Toán 11: Cho đồ thị đầy đủ có 5 đỉnh như Hình 2.9. Tìm những chu trình sơ cấp xuất phát từ đỉnh A và có: độ dài 4; độ dài 5.
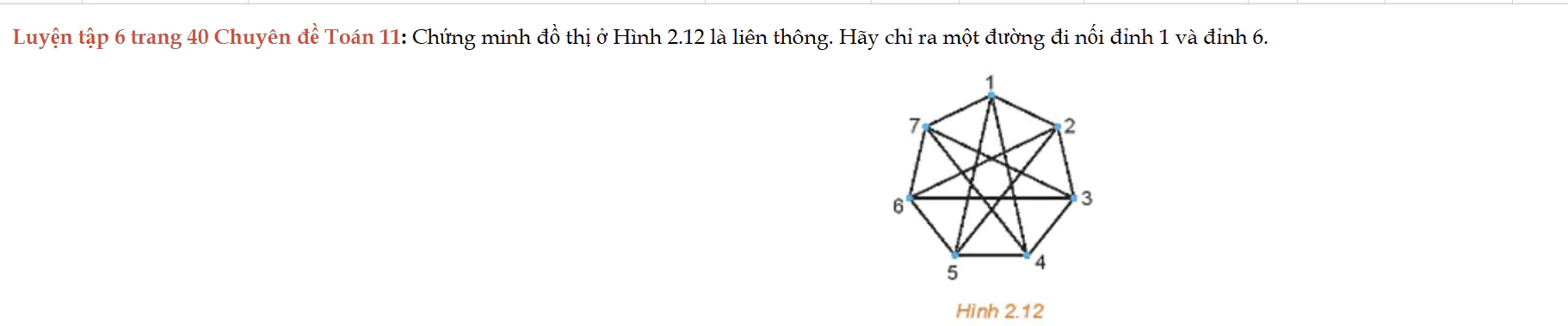
Luyện tập 6 trang 40 Chuyên đề Toán 11
Luyện tập 6 trang 40 Chuyên đề Toán 11: Chứng minh đồ thị ở Hình 2.12 là liên thông. Hãy chỉ ra một đường đi nối đỉnh 1 và đỉnh 6.
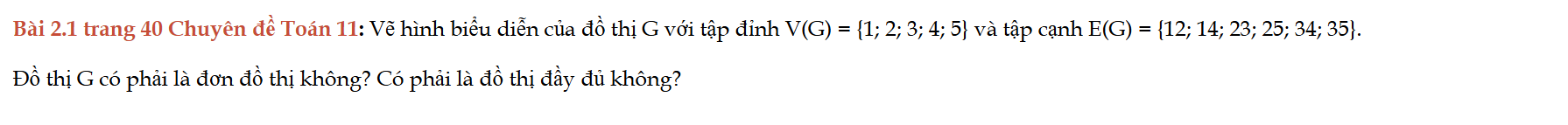
Bài 2.1 trang 40 Chuyên đề Toán 11
Bài 2.1 trang 40 Chuyên đề Toán 11: Vẽ hình biểu diễn của đồ thị G với tập đỉnh V(G) = {1; 2; 3; 4; 5} và tập cạnh E(G) = {12; 14; 23; 25; 34; 35}. Đồ thị G có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?

Bài 2.2 trang 40 Chuyên đề Toán 11
Bài 2.2 trang 40 Chuyên đề Toán 11
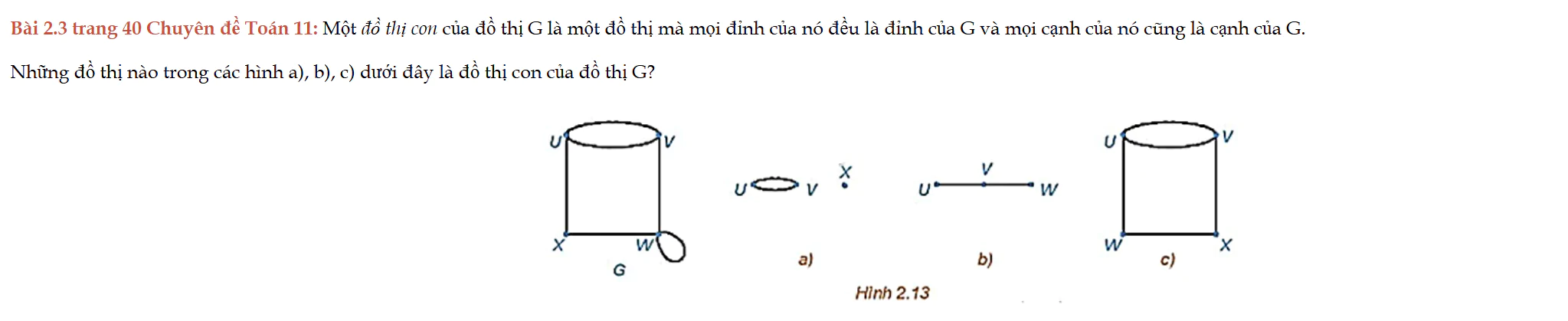
Bài 2.3 trang 40 Chuyên đề Toán 11
Bài 2.3 trang 40 Chuyên đề Toán 11: Một đồ thị con của đồ thị G là một đồ thị mà mọi đỉnh của nó đều là đỉnh của G và mọi cạnh của nó cũng là cạnh của G. Những đồ thị nào trong các hình a), b), c) dưới đây là đồ thị con của đồ thị G?
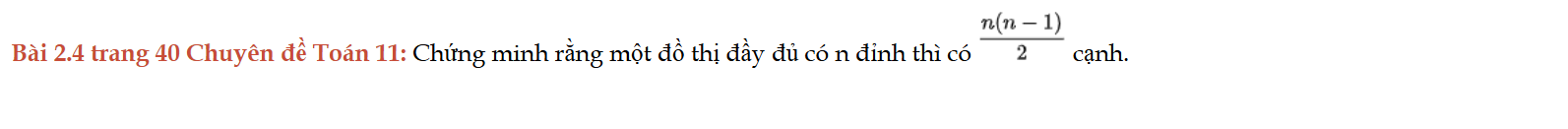
Bài 2.4 trang 40 Chuyên đề Toán 11
Bài 2.4 trang 40 Chuyên đề Toán 11

Bài 2.5 trang 40 Chuyên đề Toán 11
Bài 2.5 trang 40 Chuyên đề Toán 11: Chứng minh rằng không tồn tại đồ thị với các đỉnh có bậc là 2, 3, 3, 4, 4 và 5.
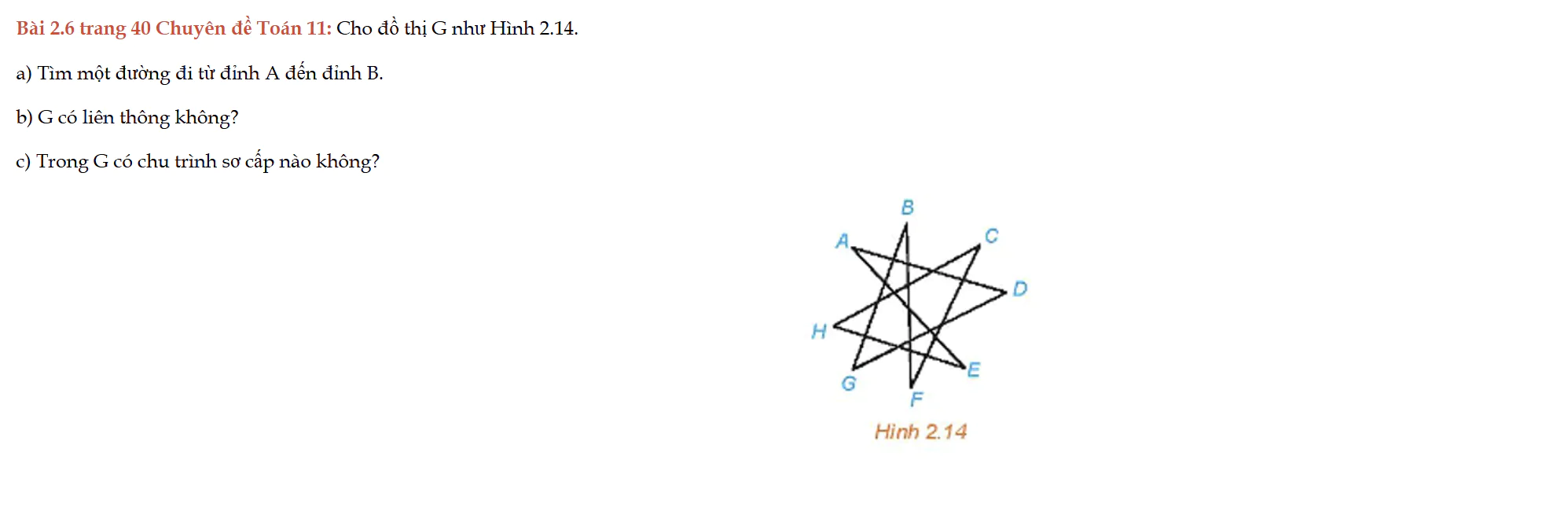
Bài 2.6 trang 40 Chuyên đề Toán 11
Bài 2.6 trang 40 Chuyên đề Toán 11: Cho đồ thị G như Hình 2.14. a) Tìm một đường đi từ đỉnh A đến đỉnh B. b) G có liên thông không? c) Trong G có chu trình sơ cấp nào không?
Giải bài tập Bài 9. Đường đi Euler và đường đi Hamilton
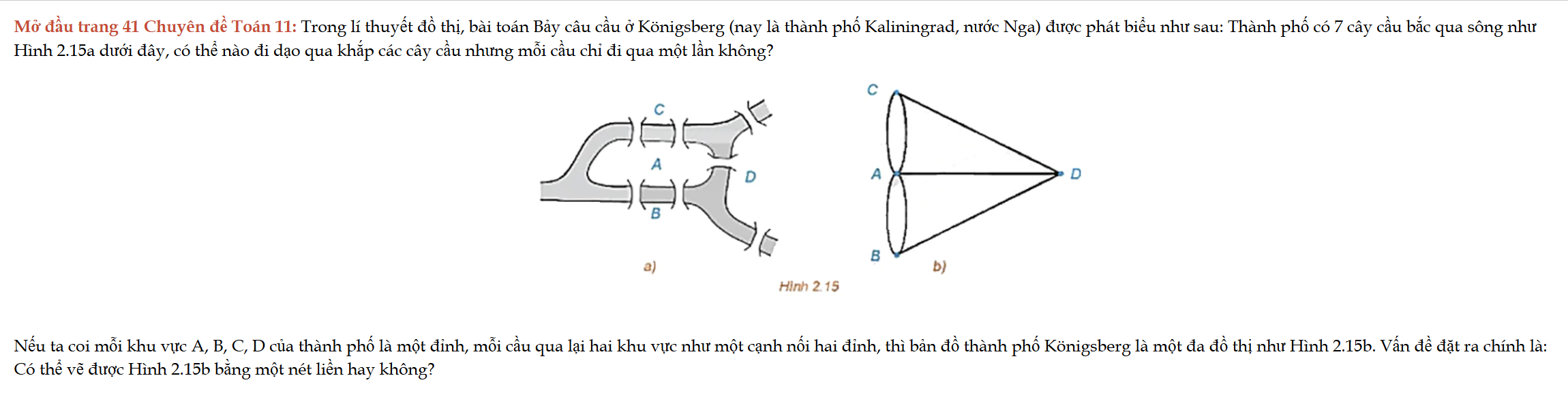
Mở đầu trang 41 Chuyên đề Toán 11
Mở đầu trang 41 Chuyên đề Toán 11
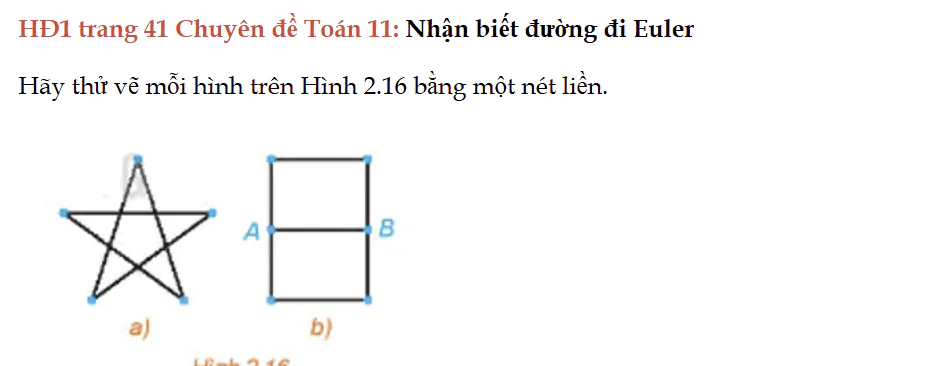
HĐ1 trang 41 Chuyên đề Toán 11
HĐ1 trang 41 Chuyên đề Toán 11: Nhận biết đường đi Euler

HĐ2 trang 43 Chuyên đề Toán 11
HĐ2 trang 43 Chuyên đề Toán 11: Nhận biết đường đi Hamilton
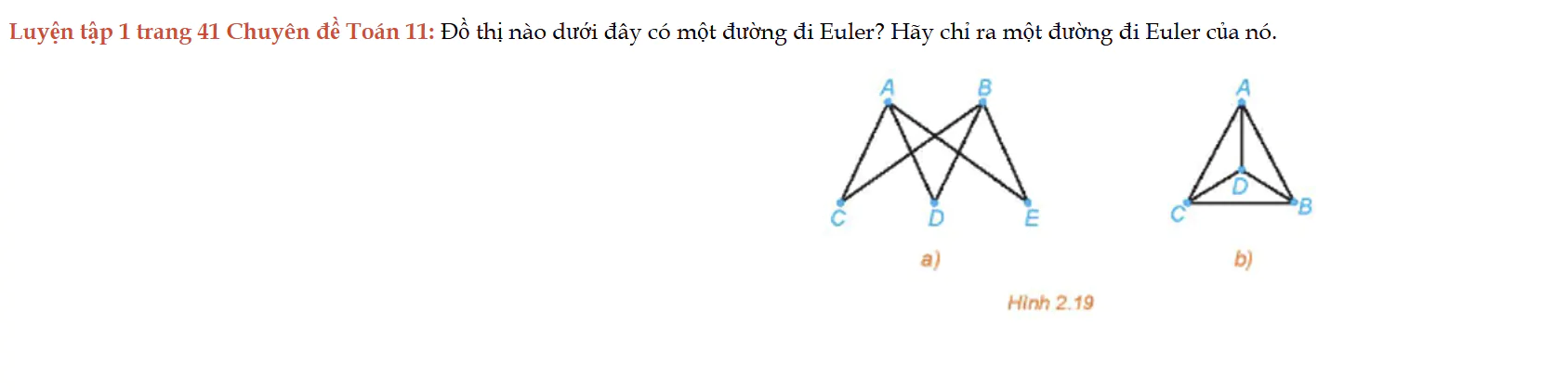
Luyện tập 1 trang 41 Chuyên đề Toán 11
Luyện tập 1 trang 41 Chuyên đề Toán 11: Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.
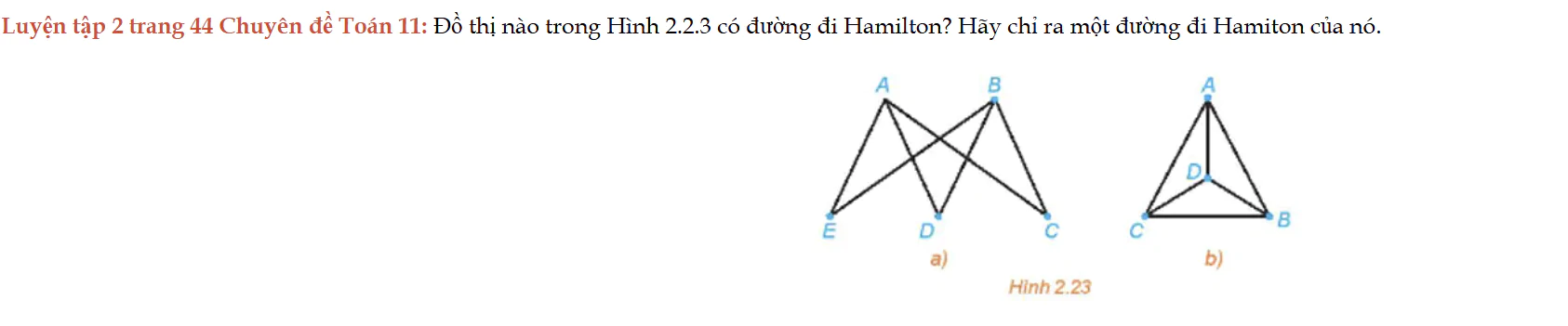
Luyện tập 2 trang 44 Chuyên đề Toán 11
Luyện tập 2 trang 44 Chuyên đề Toán 11: Đồ thị nào trong Hình 2.2.3 có đường đi Hamilton? Hãy chỉ ra một đường đi Hamiton của nó.

Bài 2.7 trang 44 Chuyên đề Toán 11
Bài 2.7 trang 44 Chuyên đề Toán 11: Mỗi đồ thị sau có một chu trình Euler hoặc một chu trình Hamilton hay không? Hãy vẽ một chu trình Euler hoặc một chu trình Hamilton khi có thể.
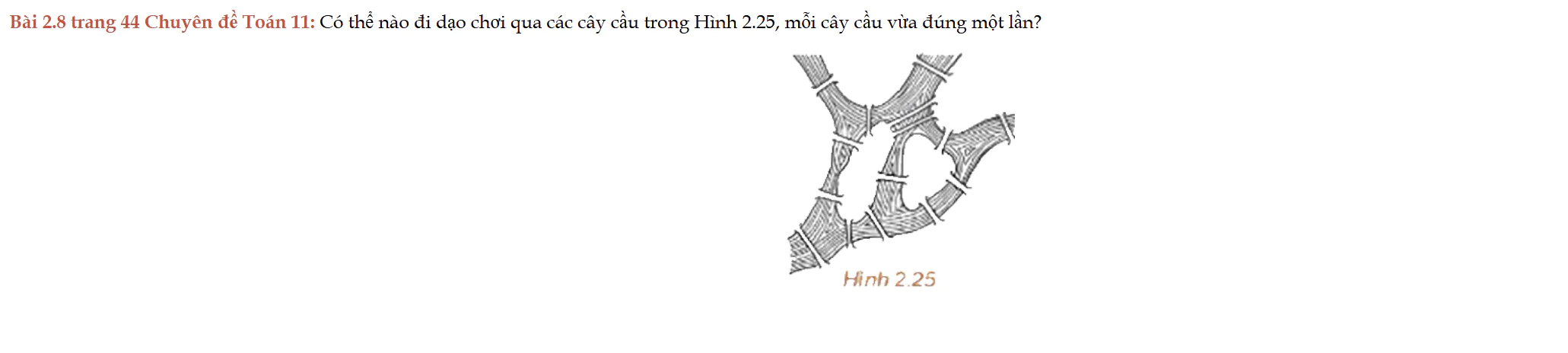
Bài 2.8 trang 44 Chuyên đề Toán 11
Bài 2.8 trang 44 Chuyên đề Toán 11: Có thể nào đi dạo chơi qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần?
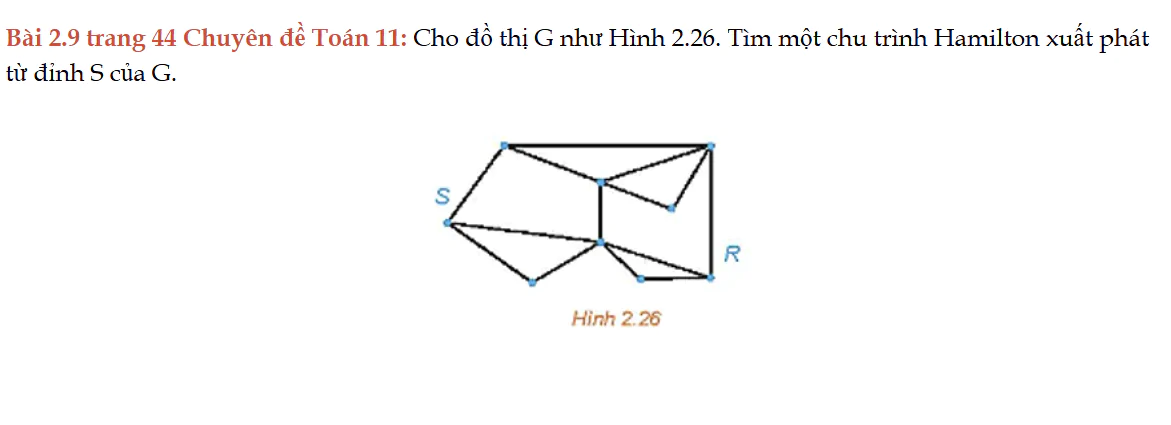
Bài 2.9 trang 44 Chuyên đề Toán 11
Bài 2.9 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.
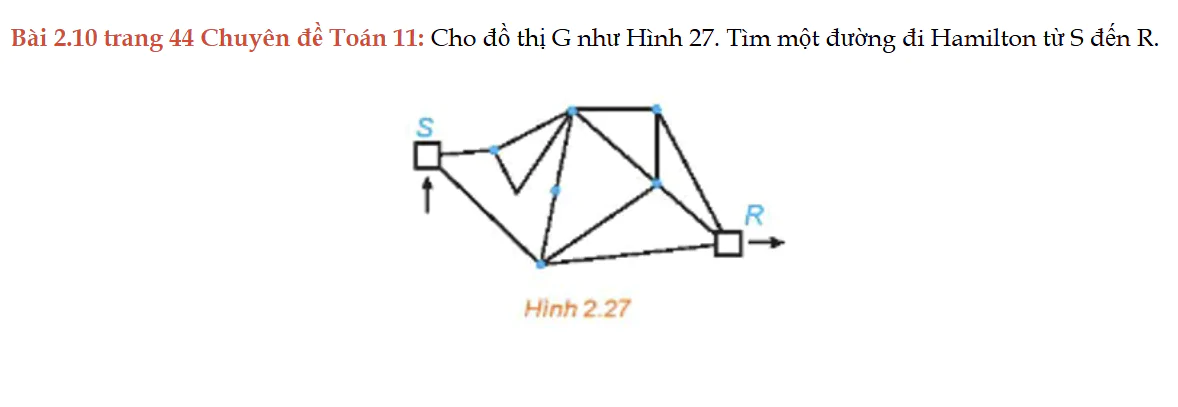
Bài 2.10 trang 44 Chuyên đề Toán 11
Bài 2.10 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 27. Tìm một đường đi Hamilton từ S đến R.

Bài 2.11 trang 45 Chuyên đề Toán 11
Bài 2.11 trang 45 Chuyên đề Toán 11

Bài 2.13 trang 45 Chuyên đề Toán 11
Bài 2.13 trang 45 Chuyên đề Toán 11: Với giá trị nào của n thì đồ thị đầy đủ Kn có một chu trình Euler? Có một đường đi Euler?

Bài 2.14 trang 45 Chuyên đề Toán 11
Bài 2.14 trang 45 Chuyên đề Toán 11: Với giá trị nào của n thì đồ thị đầy đủ Kn có một chu trình Hamilton? Có một đường đi Hamilton?
Giải bài tập Bài 10. Bài toán tìm đường đi tối ưu trong một vài trường hợp đơn giản
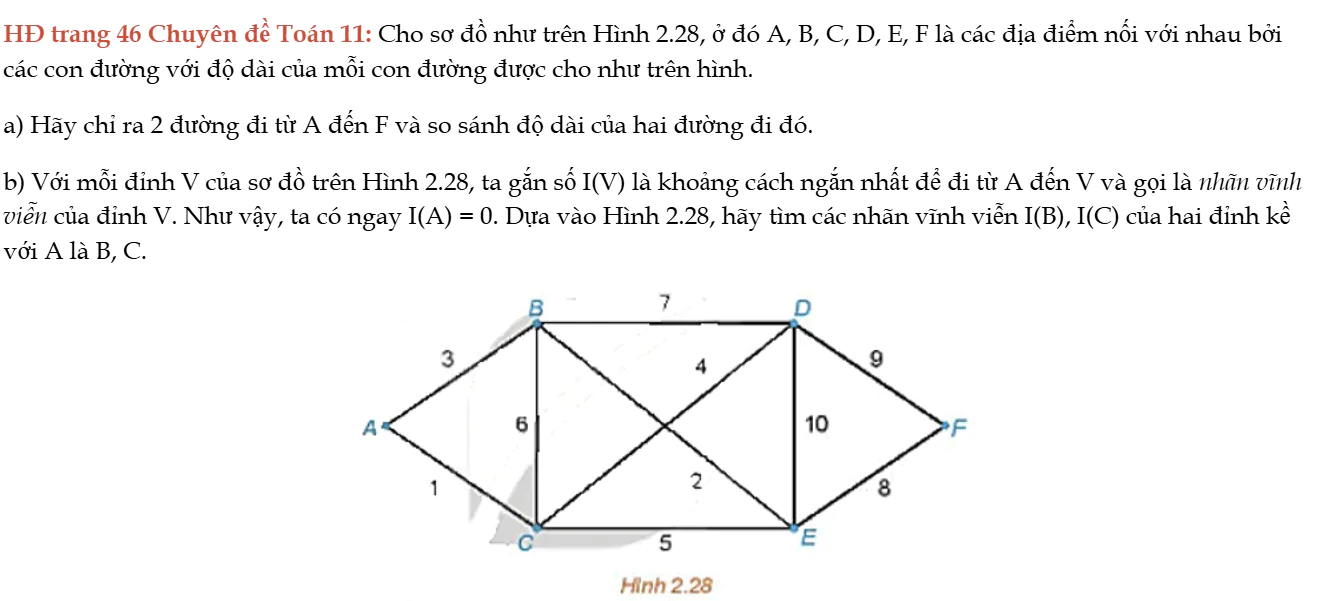
HĐ trang 46 Chuyên đề Toán 11
HĐ trang 46 Chuyên đề Toán 11
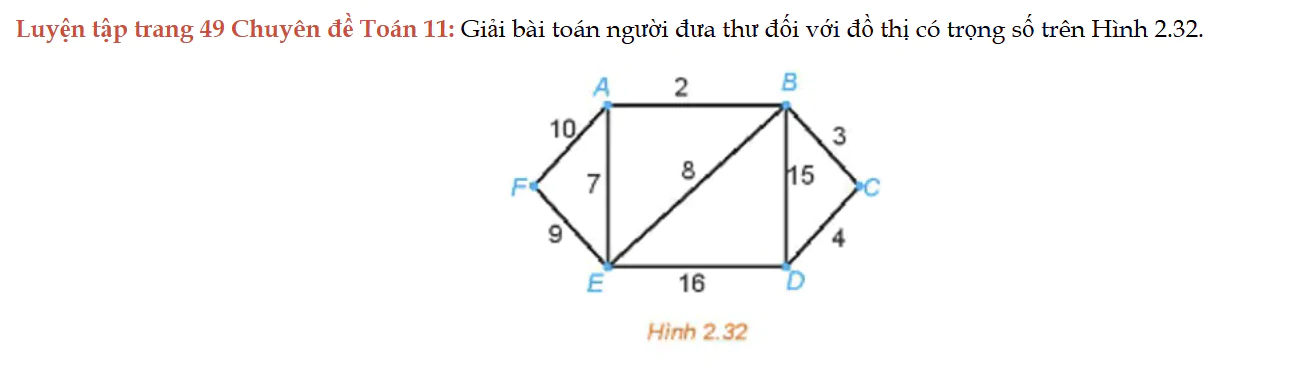
Luyện tập trang 49 Chuyên đề Toán 11
Luyện tập trang 49 Chuyên đề Toán 11: Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.32.
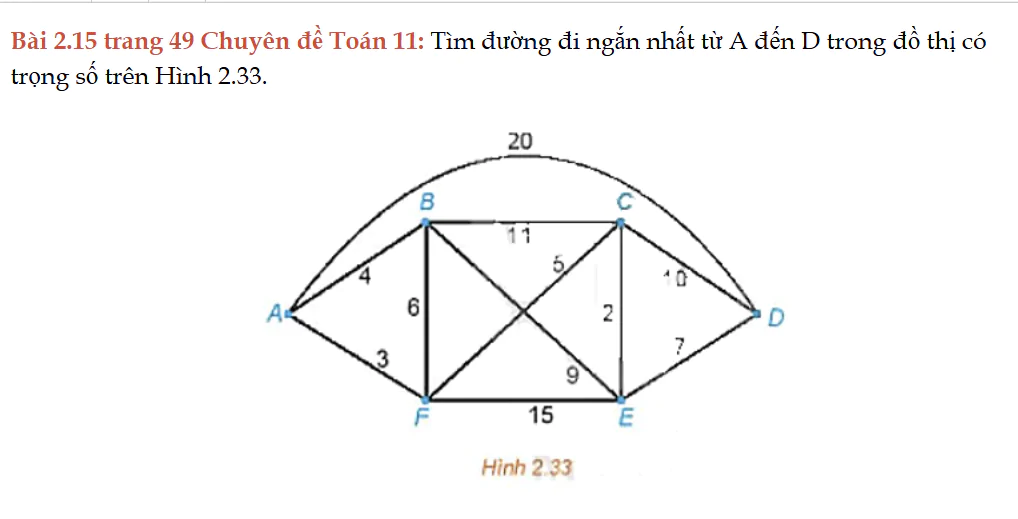
Bài 2.15 trang 49 Chuyên đề Toán 11
Bài 2.15 trang 49 Chuyên đề Toán 11
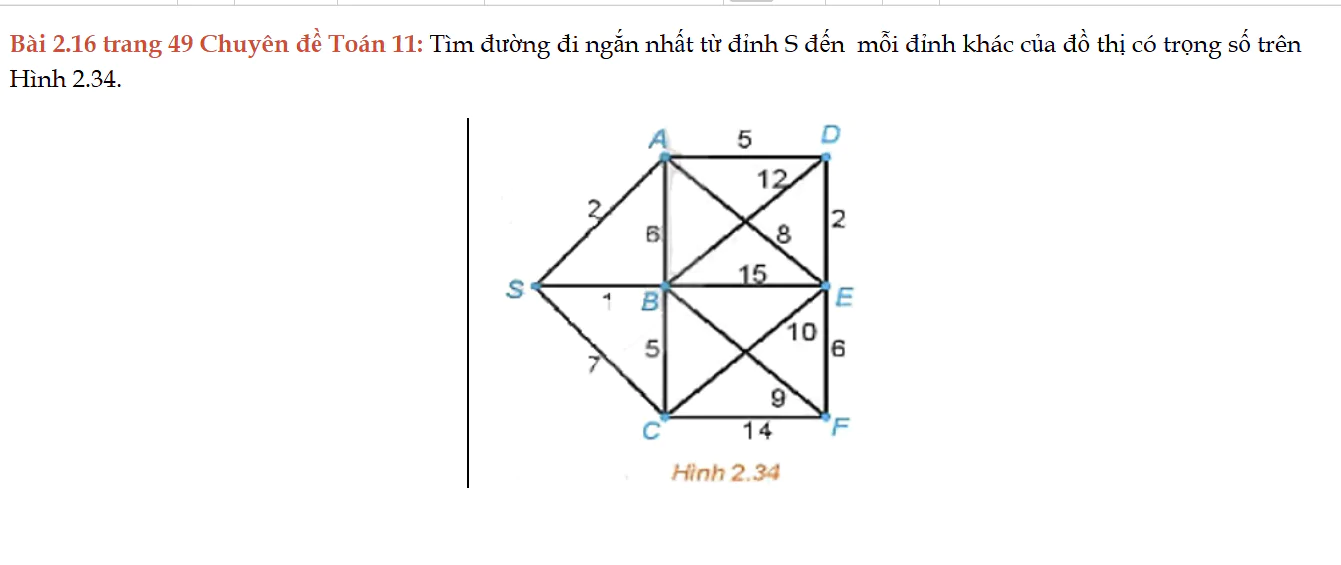
Bài 2.16 trang 49 Chuyên đề Toán 11
Bài 2.16 trang 49 Chuyên đề Toán 11: Tìm đường đi ngắn nhất từ đỉnh S đến mỗi đỉnh khác của đồ thị có trọng số trên Hình 2.34.
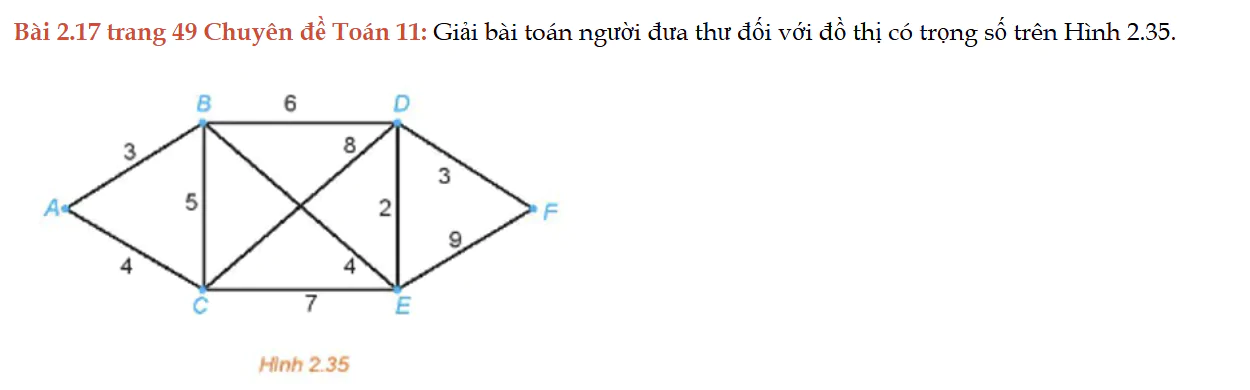
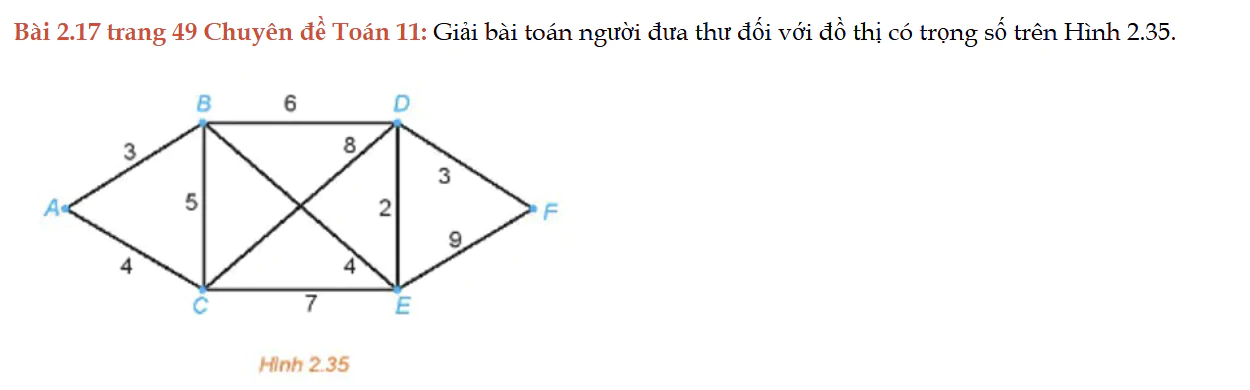
Bài 2.17 trang 49 Chuyên đề Toán 11
Bài 2.17 trang 49 Chuyên đề Toán 11: Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.35.
Bài 2.18 trang 49 Chuyên đề Toán 11
Bài 2.18 trang 49 Chuyên đề Toán 11: Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.36.
Giải bài tập Bài tập cuối chuyên đề 2
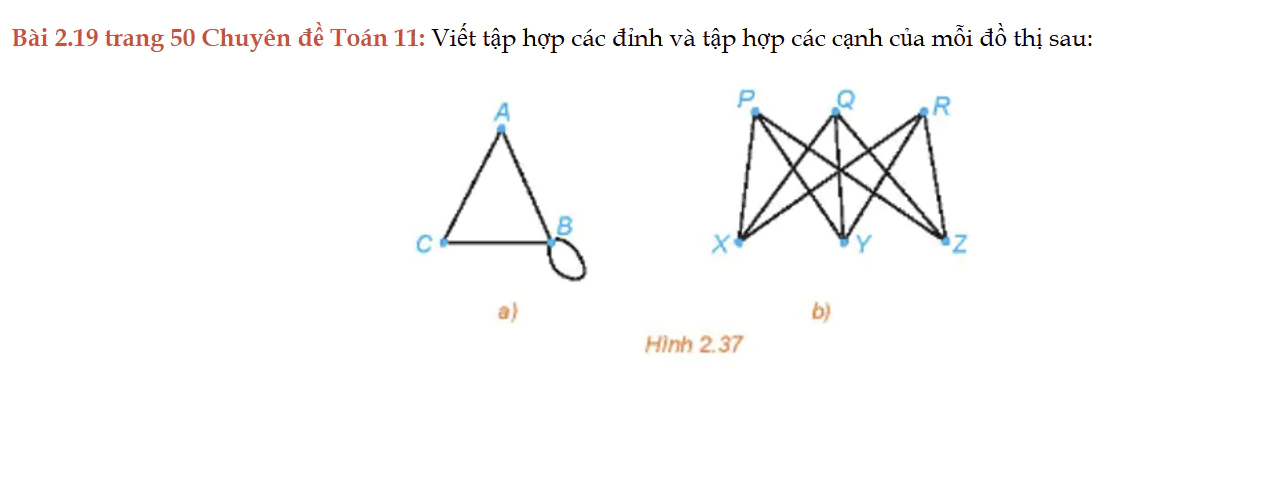
Bài 2.19 trang 50 Chuyên đề Toán 11
Bài 2.19 trang 50 Chuyên đề Toán 11: Viết tập hợp các đỉnh và tập hợp các cạnh của mỗi đồ thị sau:

Bài 2.20 trang 50 Chuyên đề Toán 11
Bài 2.20 trang 50 Chuyên đề Toán 11: Vẽ đồ thị G = (V, E) với các đỉnh và các cạnh như sau: V = {1; 2; 3; 4; 5; 6; 7; 8} và E = {12; 13; 23; 34; 35; 67; 68; 78}. Đồ thị này có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?

Bài 2.21 trang 50 Chuyên đề Toán 11
Bài 2.21 trang 50 Chuyên đề Toán 11: Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 6.

Bài 2.22 trang 50 Chuyên đề Toán 11
Bài 2.22 trang 50 Chuyên đề Toán 11: Chứng minh rằng nếu G là một đơn đồ thị có ít nhất hai đỉnh thì G có ít nhất hai đỉnh cùng bậc.

Bài 2.23 trang 50 Chuyên đề Toán 11
Bài 2.23 trang 50 Chuyên đề Toán 11: Tìm số đỉnh nhỏ nhất cần thiết để có thể xây dựng một đồ thị đầy đủ với ít nhất 1 000 cạnh.
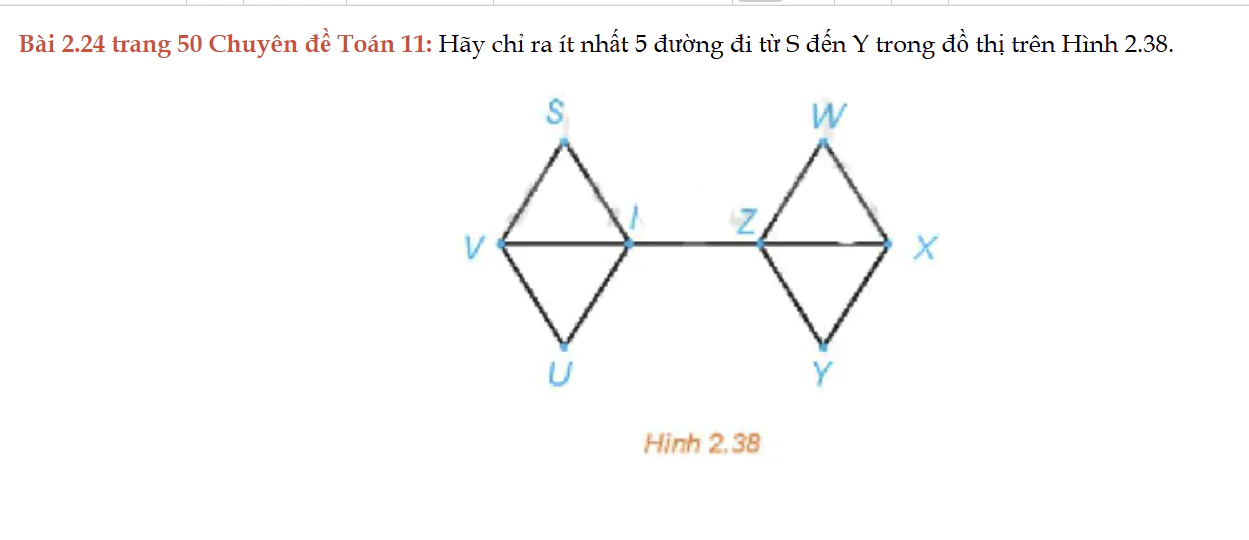
Bài 2.24 trang 50 Chuyên đề Toán 11
Bài 2.24 trang 50 Chuyên đề Toán 11: Hãy chỉ ra ít nhất 5 đường đi từ S đến Y trong đồ thị trên Hình 2.38.
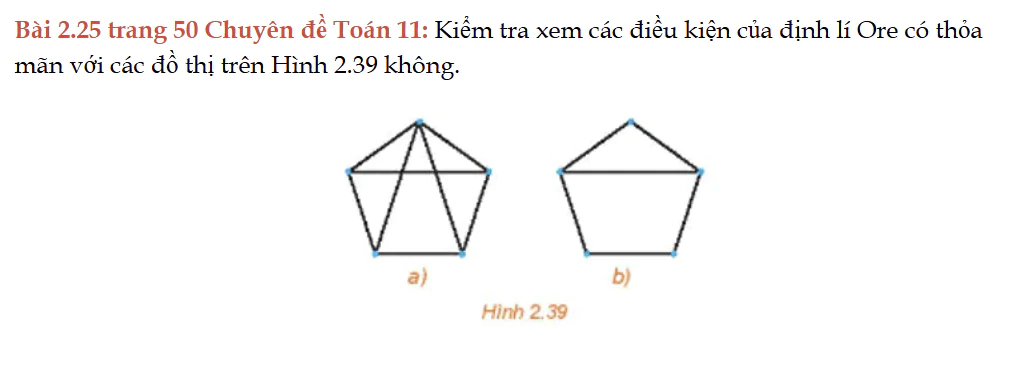
Bài 2.25 trang 50 Chuyên đề Toán 11
Bài 2.25 trang 50 Chuyên đề Toán 11: Kiểm tra xem các điều kiện của định lí Ore có thỏa mãn với các đồ thị trên Hình 2.39 không.
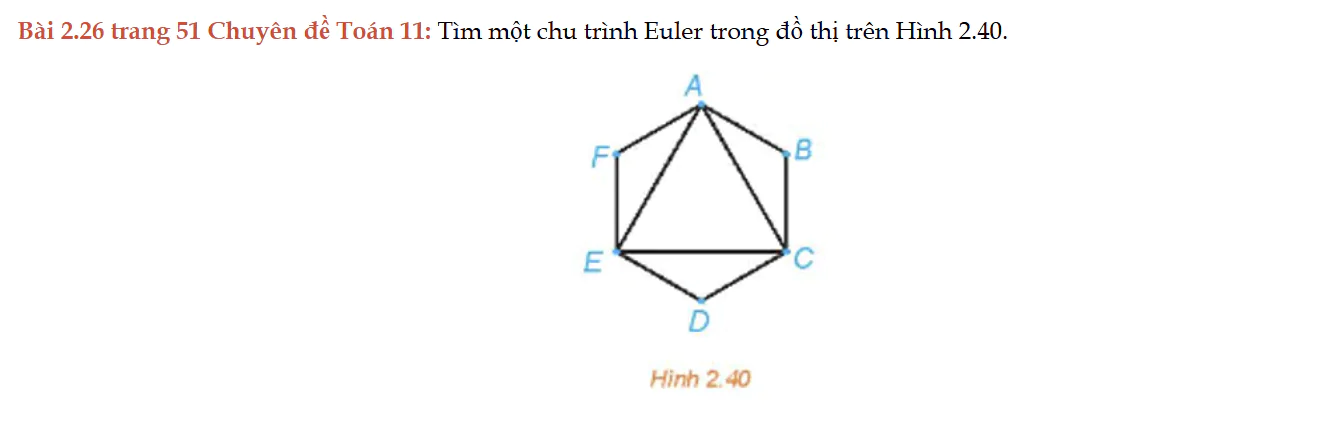
Bài 2.26 trang 51 Chuyên đề Toán 11
Bài 2.26 trang 51 Chuyên đề Toán 11: Tìm một chu trình Euler trong đồ thị trên Hình 2.40.

Bài 2.27 trang 51 Chuyên đề Toán 11
Bài 2.27 trang 51 Chuyên đề Toán 11: Giải bài toán người đưa thư với đồ thị có trọng số trên Hình 2.41.
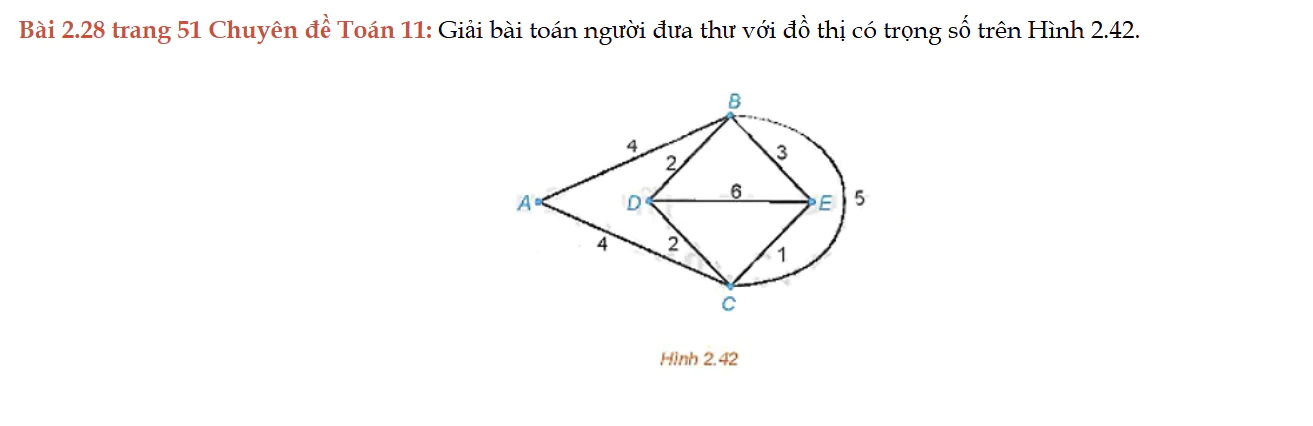
Bài 2.28 trang 51 Chuyên đề Toán 11
Bài 2.28 trang 51 Chuyên đề Toán 11: Giải bài toán người đưa thư với đồ thị có trọng số trên Hình 2.42.