Giải bài tập Bài 2.8 trang 44 Chuyên đề Toán 11 | Chuyên đề học tập Kết Nối Tri Thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 2.8 trang 44 Chuyên đề Toán 11. Bài 9. Đường đi Euler và đường đi Hamilton. Chuyên đề học tập Kết Nối Tri Thức
Đề bài:
Bài 2.8 trang 44 Chuyên đề Toán 11: Có thể nào đi dạo chơi qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần?
Đáp án và cách giải chi tiết:
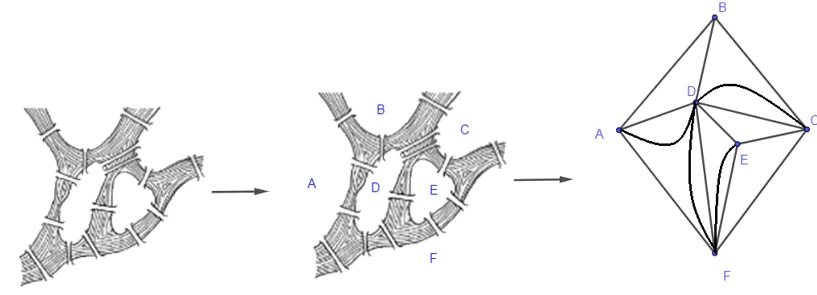
Bằng cách loaị bỏ tất cả các chi tiết ngoại trừ các vùng đất và các cây cầu, sau đó thay thế mỗi vùng đất bằng một điểm và thay thế mỗi câu cầu nối hai vùng đất bằng một đoạn nối hai điểm, ta nhận được một đồ thị G có 6 đỉnh (tương ứng 6 vùng đất) và có 15 cạnh (tương ứng 15 cây cầu) như hình vẽ trên.
Ta thấy đồ thị G liên thông và đỉnh A có bậc 4, đỉnh B có bậc 3, đỉnh C có bậc 5, đỉnh D có bậc 8, đỉnh E có bậc 4, đỉnh F có bậc 6 hay mọi đỉnh của G đều có bậc chẵn, chỉ trừ B và C có bậc lẻ, do đó theo Định lí 2, ta suy ra đồ thị G có một đường đi Euler từ A đến B. Chẳng hạn, một đường đi Euler của đồ thị G là BAFCDADFDEFECDBC.
Vậy có thể đi dạo chơi qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Mở đầu trang 41 Chuyên đề Toán 11
Mở đầu trang 41 Chuyên đề Toán 11: Trong lí thuyết đồ thị, bài toán Bảy câu cầu ở Königsberg (nay là thành phố Kaliningrad, nước Nga) được phát biểu như sau: Thành phố có 7 cây cầu bắc qua sông như Hình 2.15a dưới đây, có thể nào đi dạo qua khắp các cây cầu nhưng mỗi cầu chỉ đi qua một lần không?
Nếu ta coi mỗi khu vực A, B, C, D của thành phố là một đỉnh, mỗi cầu qua lại hai khu vực như một cạnh nối hai đỉnh, thì bản đồ thành phố Königsberg là một đa đồ thị như Hình 2.15b. Vấn đề đặt ra chính là: Có thể vẽ được Hình 2.15b bằng một nét liền hay không?
HĐ1 trang 41 Chuyên đề Toán 11
HĐ1 trang 41 Chuyên đề Toán 11: Nhận biết đường đi Euler
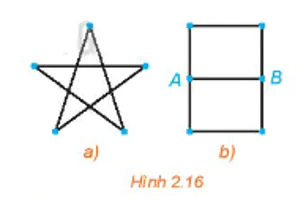
Hãy thử vẽ mỗi hình trên Hình 2.16 bằng một nét liền.
HĐ2 trang 43 Chuyên đề Toán 11
HĐ2 trang 43 Chuyên đề Toán 11: Nhận biết đường đi Hamilton
Có 5 thành phố du lịch A, B, C, D, E và các con đường nối các thành phố này như Hình 2.20. Hãy chỉ ra một cách để đi tham quan cả 5 thành phố đó, mà không cần đến địa điểm nào quá một lần.
Luyện tập 1 trang 41 Chuyên đề Toán 11
Luyện tập 1 trang 41 Chuyên đề Toán 11: Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.
Luyện tập 2 trang 44 Chuyên đề Toán 11
Luyện tập 2 trang 44 Chuyên đề Toán 11: Đồ thị nào trong Hình 2.2.3 có đường đi Hamilton? Hãy chỉ ra một đường đi Hamiton của nó.
Bài 2.7 trang 44 Chuyên đề Toán 11
Bài 2.7 trang 44 Chuyên đề Toán 11: Mỗi đồ thị sau có một chu trình Euler hoặc một chu trình Hamilton hay không? Hãy vẽ một chu trình Euler hoặc một chu trình Hamilton khi có thể.
Bài 2.9 trang 44 Chuyên đề Toán 11
Bài 2.9 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.
Bài 2.10 trang 44 Chuyên đề Toán 11
Bài 2.10 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 27. Tìm một đường đi Hamilton từ S đến R.
Bài 2.11 trang 45 Chuyên đề Toán 11
Bài 2.11 trang 45 Chuyên đề Toán 11: Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn 
trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn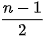 
”.
Bài 2.13 trang 45 Chuyên đề Toán 11
Bài 2.13 trang 45 Chuyên đề Toán 11: Với giá trị nào của n thì đồ thị đầy đủ Kn có một chu trình Euler? Có một đường đi Euler?
Bài 2.14 trang 45 Chuyên đề Toán 11
Bài 2.14 trang 45 Chuyên đề Toán 11: Với giá trị nào của n thì đồ thị đầy đủ Kn có một chu trình Hamilton? Có một đường đi Hamilton?