Giải bài tập Bài 4 trang 66 Toán 9 Tập 1 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 4 trang 66 Toán 9 Tập 1. Bài 1. Tỉ số lượng giác của góc nhọn. Toán 9 - Chân trời sáng tạo
Đề bài:
Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau:
a) 26°;
b) 72°;
c) 81°27'.
Đáp án và cách giải chi tiết:
Sử dụng máy tính cầm tay, ta tính được các tỉ số lượng giác như sau:
a) Tỉ số lượng giác của góc 26° là:
sin 26° ≈ 0,44; cos 26° ≈ 0,9;
tan 26° ≈ 0,49; cot 26° ≈ 2,05.
b) Tỉ số lượng giác của góc 72° là:
sin 72° ≈ 0,95; cos 72° ≈ 0,31;
tan 72° ≈ 3,08; cot 72° ≈ 0,32.
c) Tỉ số lượng giác của góc 81°27' là:
sin 81°27' ≈ 0,99; cos 81°27' ≈ 0,15;
tan 81°27' ≈ 6,65; cot 81°27' ≈ 0,15.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 60 Toán 9 Tập 1
Tại một thời điểm, khi những tia nắng chiếu, cây và bóng tạo thành các tam giác vuông như hình bên. Với 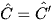 , so sánh các tỉ số
, so sánh các tỉ số  và
và  .
.

Khám phá 1 trang 60 Toán 9 Tập 1
Cho góc nhọn  . Lấy hai điểm A và A' trên On, kẻ hai đường thẳng qua A và A' vuông góc với On cắt Om lần lượt tại B và B'.
. Lấy hai điểm A và A' trên On, kẻ hai đường thẳng qua A và A' vuông góc với On cắt Om lần lượt tại B và B'.
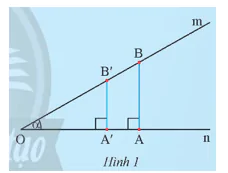
a) Có nhận xét gì về hai tam giác OAB và OA'B' ?
b) So sánh các cặp tỉ số:
 và
và 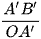 ;
;  và
và  ;
; 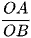 và
và 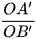 .
.
Thực hành 1 trang 61 Toán 9 Tập 1
Tính các tỉ số lượng giác của góc nhọn A trong mỗi tam giác vuông ABC có 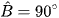 ở Hình 5 (kết quả làm tròn đến hàng phần trăm).
ở Hình 5 (kết quả làm tròn đến hàng phần trăm).

Vận dụng 1 trang 61 Toán 9 Tập 1
Sử dụng tỉ số lượng giác để giải thích tình huống trong Hoạt động khởi động (trang 60).
Tại một thời điểm, khi những tia nắng chiếu, cây và bóng tạo thành các tam giác vuông như hình bên. Với  , so sánh các tỉ số
, so sánh các tỉ số  và
và 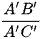 .
.

Khám phá 2 trang 62 Toán 9 Tập 1
a) Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng a (Hình 6a). Tính độ dài cạnh huyền BC theo a, rồi tính các tỉ số lượng giác của góc 45°.
b) Cho tam giác đều MNP có cạnh bằng a (Hình 6b). Tính độ dài đường cao MH theo a, rồi tính các tỉ số lượng giác của góc 30° và góc 60°.

Vận dụng 2 trang 62 Toán 9 Tập 1
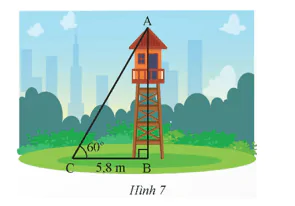
Tìm chiều cao của tháp canh trong Hình 7 (kết quả làm tròn đến hàng phần trăm).
Khám phá 3 trang 63 Toán 9 Tập 1
a) Tính các tỉ số lượng giác của góc α và của góc 90° – α trong Hình 8 theo a, b, c.

b) So sánh 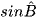 và
và  ,
,  và
và  ,
,  và
và  ,
, 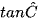 và
và  .
.
Thực hành 3 trang 63 Toán 9 Tập 1
a) So sánh: sin 72° và cos 18°; cos 72° và sin 18°; tan 72° và cot 18°.
b) Cho biết sin 18° ≈ 0,31; tan 18° ≈ 0,32. Tính cos 72° và cot 72°.
Vận dụng 3 trang 63 Toán 9 Tập 1
Tia nắng chiếu qua điểm B của nóc tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB của tòa nhà một góc y (Hình 9). Cho biết cos x ≈ 0,78 và cot x ≈ 1,25. Tính sin y và tan y (kết quả làm tròn đến hàng phần trăm).

Thực hành 4 trang 65 Toán 9 Tập 1
a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):
22°; 52°; 15°20'; 52°18'.
b) Tìm các góc nhọn x, y, z, t trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm hoặc đến phút):
sin x = 0,723; cos y = 0,828;
tan z = 3,77; cot t = 1,54.
Vận dụng 4 trang 65 Toán 9 Tập 1
a) Vẽ một tam giác vuông có một góc bằng 40°. Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40°. Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.
b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thước đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.
Bài 1 trang 66 Toán 9 Tập 1
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau:
a) BC = 5 cm; AB = 3 cm;
b) BC = 13 cm; AC = 12 cm;
c) BC = 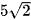 cm; AB = 5 cm;
cm; AB = 5 cm;
d) AB =  ; AC = a.
; AC = a.
Bài 3 trang 66 Toán 9 Tập 1
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:
a) sin 60°;
b) cos 75°;
c) tan 80°.
Bài 5 trang 66 Toán 9 Tập 1
Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau:
a) cos α = 0,6;
b) tan α =  .
.
Bài 6 trang 66 Toán 9 Tập 1
Tia nắng chiếu qua nóc của một tòa nhà hợp với mặt đất một góc α. Cho biết tòa nhà cao 21 m và bóng của nó trên mặt đất dài 15 m (Hình 10). Tính góc α (kết quả làm tròn đến độ).

Bài 7 trang 66 Toán 9 Tập 1
Một cái thang 12 m được đặt vào một bức tường sao cho chân thang cách tường 7 m (Hình 11). Tính góc α tạo bởi thang và tường.


