Giải bài tập Bài 3 trang 10 Toán 9 Tập 2 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 10 Toán 9 Tập 2. Bài 1. Hàm số và đồ thị của hàm số y = ax² (a ≠ 0). Toán 9 - Chân trời sáng tạo
Đề bài:
Cho hai hàm số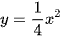 
và 
. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Oxy.
Đáp án và cách giải chi tiết:
Ta có bảng giá trị của hàm số:
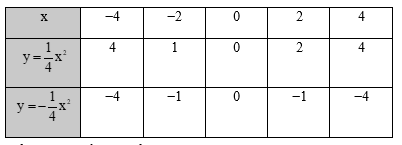
Trên mặt phẳng tọa độ, lấy các điểm A(−4; 4), B(−2; 1), O(0; 0), C(2; 1), D(4; 4),
A'(−4; −4), B'(−2; −1), C'(2; −1), D'(4; −4).
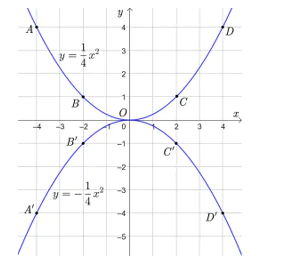
• Đồ thị hàm số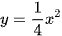 
là một đường parabol đỉnh O, đi qua các điểm A(−4; 4), B(−2; 1), O(0; 0), C(2; 1), D(4; 4).
• Đồ thị hàm số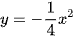 
là một đường parabol đỉnh O, đi qua các điểm A'(−4; −4), B'(−2; −1), O(0; 0), C'(2; −1), D'(4; −4).
Ta có đồ thị của hai hàm số hai hàm số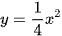 
và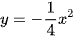 
được vẽ trên cùng một mặt phẳng tọa độ Oxy như sau:
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 6 Toán 9 Tập 2
Một vật được thả rơi tự do từ độ cao 45 m. Quãng đường chuyển động s (m) của vật theo thời gian rơi t (giây) được cho bởi công thức s = 5t2. Sau khi thả 2 giây, quãng đường vật di chuyển được là bao nhiêu mét?
Khám phá 1 trang 6 Toán 9 Tập 2
Diện tích S của hình tròn được tính bởi công thức S = πR2, trong đó R là bán kính của hình tròn và π ≈ 3,14.
a) Diện tích S của hình tròn với R = 10 cm.
b) Diện tích S có phải là hàm số của biến số R không?
Thực hành 1 trang 7 Toán 9 Tập 2
a) Xác định hệ số của x2 trong các hàm số sau: y = 0,75x2; y = −3x2;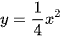 
.
b) Với mỗi hàm số đã cho ở câu a), tính giá trị của y khi x = −2; x = 2.
Vận dụng 1 trang 7 Toán 9 Tập 2
Gọi x (cm) là chiều dài cạnh của một viên gạch lát nền hình vuông.
a) Viết công thức tính diện tích S (cm2) của viên gạch đó.
b) Tính S khi x = 20; x = 30; x = 60.
Khám phá 2 trang 7 Toán 9 Tập 2
Cho hàm số 
.
Hoàn thành bảng giá trị sau:
Thực hành 2 trang 8 Toán 9 Tập 2
Lập bảng giá trị của hai hàm số 
và 
với x lần lượt bằng -4; -2; 0; 2; 4.
Vận dụng 2 trang 8 Toán 9 Tập 2
Một vật rơi tự do từ độ cao 125 m so với mặt đất. Quãng đường chuyển động s (m) của vật phụ thuộc vào thời gian t (giây) được cho bởi công thức s = 5t2.
a) Sau 2 giây, vật này cách mặt đất bao nhiêu mét? Tương tự, sau 3 giây vật này cách mặt đất bao nhiêu mét?
b) Sau bao lâu thì vật này tiếp đất?
Khám phá 3 trang 8 Toán 9 Tập 2
Cho hàm số y = x2. Ta lập bảng giá trị sau:
Từ bảng trên, ta lấy các điểm A(−3; 9), B(−2; 4), C(−1; 1), O(0; 0), C'(1; 1), B'(2; 4), A'(3; 9) trên mặt phẳng tọa độ Oxy. Đồ thị hàm số y = x2 là một đường cong đi qua các điểm nêu trên và có dạng như Hình 2.
Từ đồ thị ở Hình 2, hãy trả lời các câu hỏi sau:
a) Đồ thị của hàm số có vị trí như thế nào so với trục hoành?
b) Có nhận xét gì về vị trí của các cặp điểm A và A', B và B', C và C' so với trục tung?
c) Điểm nào là điểm thấp nhất của đồ thị?
Khám phá 4 trang 8 Toán 9 Tập 2
Cho hàm số 
.
a) Lập bảng giá trị của hàm số khi x lần lượt nhận các giá trị −2; −1; 0; 1; 2.
b) Vẽ đồ thị của hàm số. Có nhận xét gì về đồ thị của hàm số đó?
Vận dụng 3 trang 10 Toán 9 Tập 2
Động năng (tính bằng J) của một quả bưởi nặng 1 kg rơi với vận tốc v (m/s) được tính bằng công thức 
.
a) Tính động năng của quả bưởi đạt được khi nó rơi với tốc độ lần lượt là 3 m/s, 4 m/s.
b) Tính tốc độ rơi của quả bưởi tại thời điểm quả bưởi đạt được động năng 32 J.
Bài 1 trang 10 Toán 9 Tập 2
Cho hàm số y = −x2.
a) Lập bảng giá trị của hàm số.
b) Vẽ đồ thị của hàm số.
Bài 2 trang 10 Toán 9 Tập 2
Cho hàm số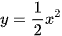 
.
a) Vẽ đồ thị của hàm số.
b) Trong các điểm A(-6; 8), B(6; 8),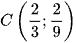 
, điểm nào thuộc đồ thị của hàm số trên?
Bài 4 trang 10 Toán 9 Tập 2
Cho hàm số y = ax2 (a ≠ 0).
a) Tìm a, biết đồ thị của hàm số đi qua điểm M(2; 6).
b) Vẽ đồ thị của hàm số với a vừa tìm được.
c) Tìm các điểm thuộc đồ thị của hàm số có tung độ y = 9.
Bài 5 trang 10 Toán 9 Tập 2
Cho một hình lập phương có độ dài cạnh x (cm).
a) Viết công thức tính diện tích toàn phần S (cm2) của hình lập phương theo x.
b) Lập bảng giá trị của hàm số S khi x lần lượt nhận các giá trị: 
, 1,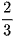 
, 2, 3.
c) Tính độ dài cạnh của hình lập phương, biết S = 54 cm2.
Bài 6 trang 10 Toán 9 Tập 2
Khi gió thổi vuông góc vào cánh buồm của một con thuyền thì lực F (N) của nó tỉ lệ thuận với bình phương tốc độ v (m/s) của gió, tức là F = av2 (a là hằng số). Biết rằng khi tốc độ của gió bằng 3 m/s thì lực tác động lên cánh buồm bằng 180 N.
a) Tính hằng số a.
b) Với a vừa tìm được, tính lực F khi v = 15 m/s và khi v = 26 m/s.
c) Biết rằng cánh buồm chỉ có thể chịu được một lực