Giải bài tập Bài 2 trang 34 Toán 9 Tập 1 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 2 trang 34 Toán 9 Tập 1. Bài tập cuối chương 2.. Toán 9 - Chân trời sáng tạo
Đề bài:
Bài 2 trang 34 Toán 9 Tập 1: Cho các số thực x, y, z biết 
. Khẳng định nào sau đây sai?
A. 
.
B. 
nếu z âm.
C.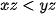 
nếu z dương.
D. 
.
Đáp án và cách giải chi tiết:
Đáp án đúng là: B
Vớ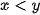i
thì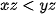 
nếu z âm.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 34 Toán 9 Tập 1
Bài 1 trang 34 Toán 9 Tập 1: Bất đẳng thức n ≤ 3 có thể được phát biểu là
A. n lớn hơn 3.
B. n nhỏ hơn 3.
C. n không nhỏ hơn 3.
D. n không lớn hơn 3.
Bài 3 trang 35 Toán 9 Tập 1
Bài 3 trang 35 Toán 9 Tập 1: Hệ thức nào sau đây là bất đẳng thức?
A. 
.
B.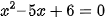 
.
C.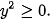
D. 
.
Bài 4 trang 35 Toán 9 Tập 1
Bài 4 trang 35 Toán 9 Tập 1: Bất phương trình 
có nghiệm là
A. 
.
B. 
.
C. 
.
D. 
.
Bài 5 trang 35 Toán 9 Tập 1
Bài 5 trang 35 Toán 9 Tập 1: Bất phương trình 
có nghiệm là
A. 
.
B. 
.
C.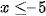 
.
D.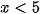 
.
Bài 6 trang 35 Toán 9 Tập 1
Bài 6 trang 35 Toán 9 Tập 1: Cho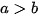 
, chứng minh:
a) 
;
b) 
;
c) 
;
d)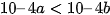 
.
Bài 7 trang 35 Toán 9 Tập 1
Bài 7 trang 35 Toán 9 Tập 1: Giải các bất phương trình sau:
a) 
;
b) 
c) 
;
d) 
Bài 8 trang 35 Toán 9 Tập 1
Bài 8 trang 35 Toán 9 Tập 1: Tìm x sao cho:
a) Giá trị của biểu thức 
không nhỏ hơn giá trị của biểu thức 
;
b) Giá trị của biểu thức không lớn hơn giá trị của biểu thức .
Bài 9 trang 35 Toán 9 Tập 1
Bài 9 trang 35 Toán 9 Tập 1: Trong cuộc thi “Đố vui để học”, mỗi thí sinh phải trả lời 12 câu hỏi của ban tổ chức. Mỗi câu hỏi gồm bốn phương án, trong đó chỉ có một phương án đúng. Với mỗi câu hỏi, nếu trả lời đúng thì được cộng 5 điểm, trả lời sai bị trừ 2 điểm. Khi bắt đầu cuộc thi, mỗi thí sinh có sẵn 20 điểm. Thí sinh nào đạt từ 50 điểm trở lên sẽ được vào vòng thi tiếp theo. Hỏi thí sinh phải trả lời đúng ít nhất bao nhiêu câu thì được vào vòng thi tiếp theo?
Bài 10 trang 35 Toán 9 Tập 1
Bài 10 trang 35 Toán 9 Tập 1: Tìm lỗi sai trong các lời giải sau:
a) Giải bất phương trình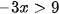 
.
Ta có: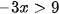
.
Vậy nghiệm của bất phương trình là .
b) Giải bất phương trình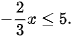 
Ta có: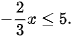
Vậy nghiệm của bất phương trình là .