Giải bài tập Vận dụng trang 91 Toán 9 Tập 2 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Vận dụng trang 91 Toán 9 Tập 2. Bài 2. Hình nón. Toán 9 - Chân trời sáng tạo
Đề bài:
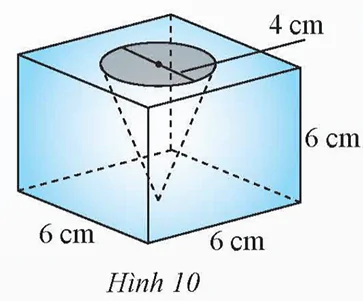
Từ một khối gỗ có dạng hình lập phương cạnh 6 cm, người ta khoét một hình nón có đường kính mặt đáy là 4 cm và đỉnh của hình nón chạm vào mặt đáy của khối gỗ (Hình 10). Hãy tính thể tích của phần khối gỗ còn lại (kết quả làm tròn đến hàng đơn vị).
Đáp án và cách giải chi tiết:
Thể tích khối lập phương là: V1 = 63 = 216 (cm3).
Bán kính mặt đáy của phần khoét hình nón là:
r =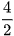 
= 2 (cm).
Thể tích phần khoét hình nón là:
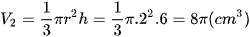
Thể tích khối gỗ còn lại là:
V = V1 – V2 = 216 – 8π ≈ 191 (cm3).
Vậy thể tích của phần khối gỗ còn lại khoảng 191 cm3.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 2 trang 92 Toán 9 Tập 2
Hãy cho biết chiều cao, bán kính đáy, độ dài đường sinh và diện tích xung quanh của mỗi hình nón sau:
Bài 3 trang 92 Toán 9 Tập 2
Tạo lập hình nón có bán kính đáy bằng 4 cm, chiều cao 7 cm.
Bài 4 trang 92 Toán 9 Tập 2
Tính thể tích của hình nón biết:
a) Bán kính đáy 6 cm, chiều cao 12 cm;
b) Đường kính của mặt đáy là 7 m, chiều cao 10 m;
c) Diện tích đáy 152 cm2, chiều cao 6 cm;
d) Chu vi đáy 130 cm, chiều cao 24 cm.
Bài 5 trang 92 Toán 9 Tập 2
Một cái mũ chú hề có kích thước như Hình 13. Hãy tính tổng diện tích giấy làm nên chiếc mũ (không tính phần hao hụt, kết quả làm tròn đến hàng đơn vị).
Khởi động trang 88 Toán 9 Tập 2
Vỏ kem ốc quế, chao đèn trang trí, chiếc nón lá ở hình bên có đặc điểm gì chung?
Tìm một số vật thể trong thực tế có hình dạng tương tự.
Khám phá 1 trang 88 Toán 9 Tập 2
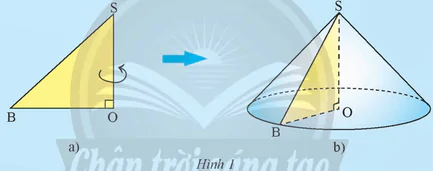
Cho tấm bìa có dạng hình tam giác OSB vuông tại O, cạnh SO cố định (Hình 1a). Khi quay tấm bìa một vòng quanh cạnh SO thì hình tạo ra giống với đồ vật quen thuộc nào?
Thực hành 1 trang 89 Toán 9 Tập 2
Chiếc mũ ở Hình 4 có dạng hình nón. Cho biết bán kính đáy, chiều cao và độ dài đường sinh của hình nón đó.
Thực hành 2 trang 89 Toán 9 Tập 2
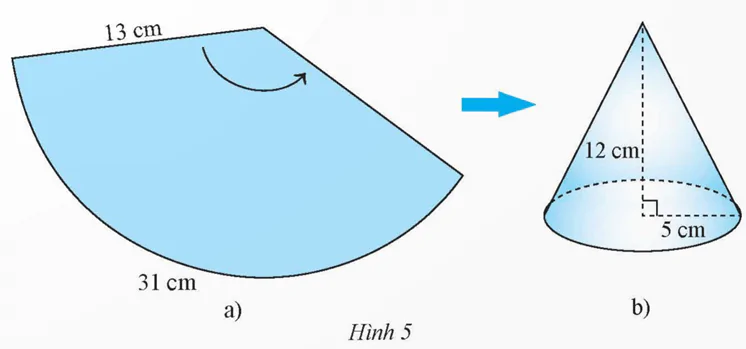
Tạo lập hình nón có chiều cao 12 cm và bán kính đáy 5 cm theo hướng dẫn sau:
− Cắt tấm bìa hình quạt tròn có bán kính bằng độ dài đường sinh l = 
= 13 (cm), độ dài cung của hình quạt tròn bằng 10π cm ≈ 31 cm (Hình 5a).
− Cắt tấm bìa hình tròn bán kính 5 cm.
− Ghép và dán hai mép quạt lại với nhau sao cho cung của nó tạo thành đường tròn, rồi dán tấm bìa hình tròn ở trên vào làm đáy, ta được hình nón như Hình 5b.
Khám phá 2 trang 90 Toán 9 Tập 2
Cho một hình nón có bán kính r, có độ dài đường sinh l (Hình 6a). Cắt mặt xung quanh của hình nón theo một đường sinh của nó rồi trải phẳng ra, ta được hình quạt tròn (Hình 6b). Tính theo r và l:
a) Độ dài cung BB';
b) Số đo cung BB';
c) Diện tích của hình quạt tròn.
Thực hành 3 trang 90 Toán 9 Tập 2
Tính diện tích xung quanh và diện tích toàn phần của hình nón có đường kính đáy d = 10 m và chiều cao h = 12 m (kết quả làm tròn đến hàng phần trăm).
Khám phá 3 trang 91 Toán 9 Tập 2
Lấy một cái gàu hình nón và một cái bình hình trụ (Hình 8a) có cùng bán kính đáy r và chiều cao h. Múc đầy nước vào gàu rồi đổ qua cái bình. Sau ba lần đổ nước như thế thì cái bình vừa đầy nước (Hình 8b). Tính theo r và h:
a) Thể tích của bình hình trụ;
b) Thể tích của gàu hình nón.
Thực hành 4 trang 91 Toán 9 Tập 2
Tính thể tích của hình nón có bán kính đáy 6 cm, chiều cao 4 cm.
