Giải bài tập Thực hành 4 trang 49 Toán 11 Tập 1 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Thực hành 4 trang 49 Toán 11 Tập 1. Bài 1: Dãy số. Toán 11 - Chân trời sáng tạo
Đề bài:
Xét tính bị chặn của các dãy số sau:
a) (an) với ;
b) (bn) với .
Đáp án và cách giải chi tiết:
a) Vì nên , ∀n ∈ ℕ*.
Do đó dãy số (an) bị chặn trên và chặn dưới.
Vì vậy dãy số (an) bị chặn.
b) Ta có:
Vì n ∈ ℕ* nên nên hay bn < 1.
Vì n ∈ ℕ* nên hay bn > 0.
Suy ra 0 < bn < 1. Do đó (bn) là dãy bị chặn trên và chặn dưới.
Vì vậy dãy số (bn) bị chặn.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 50 Toán 11 Tập 1
Bài 1 trang 50 Toán 11 Tập 1: Tìm u2, u3 và dự đoán công thức số hạng tổng quát của un dãy số:
Bài 2 trang 50 Toán 11 Tập 1
Bài 2 trang 50 Toán 11 Tập 1: Cho dãy số (un) với . Tìm u1, u2, u3 và dự đoán công thức số hạng tổng quát của un.
Bài 3 trang 50 Toán 11 Tập 1
Bài 3 trang 50 Toán 11 Tập 1: Xét tính tăng, giảm của dãy số (yn) với
Bài 4 trang 50 Toán 11 Tập 1
Bài 4 trang 50 Toán 11 Tập 1: Xét tính bị chặn của các dãy số sau:
a) (an) với
b) (un) với
Bài 5 trang 50 Toán 11 Tập 1
Bài 5 trang 50 Toán 11 Tập 1: Cho dãy số (un) với . Chứng minh (un) là dãy số tăng và bị chặn.
Bài 6 trang 50 Toán 11 Tập 1
Bài 6 trang 50 Toán 11 Tập 1: Cho dãy số (un) với . Tìm các giá trị của a để:
a) (un) là dãy số tăng;
b) (un) là dãy số giảm.
Bài 7 trang 50 Toán 11 Tập 1
Bài 7 trang 50 Toán 11 Tập 1: Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đó từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
Hoạt động khởi động trang 45 Toán 11 Tập 1
Gọi u1; u2; u3; ...; un lần lượt là diện tích các tình huống có độ dài cạnh là 1; 2; 3; ...; n. Tính u3 và u4.
Hoạt động khám phá 1 trang 45 Toán 11 Tập 1
Cho hàm số:
u: N* R
n u(n) = n2.
Tính u(1), u(2), u(50), u(100).
Hoạt động khám phá 2 trang 46 Toán 11 Tập 1
Cho hàm số:
v: {1;2;3;4;5} R
n v(n) = 2n.
Tính v(1), v(2), v(3), v(4), v(5).
Thực hành 1 trang 46 Toán 11 Tập 1
Cho dãy số:
u: N* R
n un = n3.
a) Hãy cho biết dãy số trên là hữu hạn hay vô hạn.
b) Viết năm số hạng đầu tiên của dãy số đã cho
Vận dụng 1 trang 46 Toán 11 Tập 1
Cho 5 hình tròn theo thứ tự có bán kính 1; 2; 3; 4; 5.
a) Viết dãy số chỉ diện tích của 5 hình tròn này.
b) Tìm số hạng đầu và số hạng cuối của dãy số trên.
Hoạt động khám phá 3 trang 46 Toán 11 Tập 1
Cho các dãy số (an), (bn), (cn), (dn) được xác định như sau:
+) a1 = 0; a2 = 1; a3 = 2; a4 = 3; a5 = 4.
+) bn = 2n.
+) 
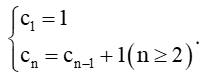
+) dn là chu vi của đường tròn có bán kính n.
Tính bốn số hạng đầu tiên của các dãy số trên.
Thực hành 2 trang 47 Toán 11 Tập 1
Cho dãy số (un) xác định bởi: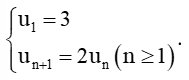 
a) Chứng minh u2 = 2.3; u3 = 22.3; u4 = 23.3.
b) Dự đoán công thức số hạng tổng quát của dãy số (un).
Vận dụng 2 trang 47 Toán 11 Tập 1
Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1 cột dỗ (Hình 1). Gọi un là số cột gỗ nằm ở lớp thứ n tính từ trên xuống và cho biết lớp trên cùng có 14 cột gỗ. Hãy xác định dãy số (un) bằng hai cách:
a) Viết công thức số hạng tổng quát un.
b) Viết hệ thức truy hồi.
Hoạt động khám phá 4 trang 48 Toán 11 Tập 1
Cho hai dãy số (an) và (bn) được xác định như sau: an = 3n + 1, bn = – 5n.
a) So sánh an và an + 1, ∀n ∈ ℕ*.
b) So sánh bn và bn + 1, ∀n ∈ ℕ*.
Thực hành 3 trang 48 Toán 11 Tập 1
Xét tính tăng, giảm của các dãy số sau:
a) (un) với ;
b) (xn) với ;
c) (tn) với tn = (– 1)n . n2.
Vận dụng 3 trang 49 Toán 11 Tập 1
Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp nhau hơn kém nhau 1 cột gỗ (Hình 2).
a) Gọi u1 = 25 là số cột gỗ có ở hàng dưới cùng của chồng cột gỗ, un là số cột gỗ có ở hàng thứ n tính từ dưới lên trên. Xét tính tăng, giảm của dãy số này.
b) Gọi vt = 14 là số cột gỗ có ở hàng trên cùng của chồng cột gỗ, vn là số cột gỗ có ở hàng thứ n tính từ trên xuống dưới. Xét tính tăng, giảm của dãy số này.
Hoạt động khám phá 5 trang 49 Toán 11 Tập 1
Cho dãy số (un) với . So sánh các số hạng của dãy số với 0 và 1.