Giải bài tập Khám phá 2 trang 85 Toán 9 Tập 2 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Khám phá 2 trang 85 Toán 9 Tập 2. Bài 1. Hình trụ. Toán 9 - Chân trời sáng tạo
Đề bài:
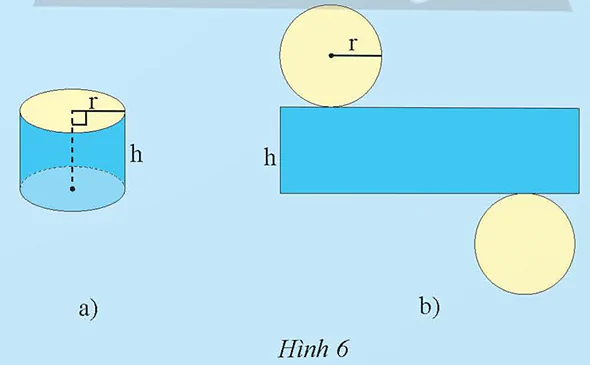
Hình khai triển của một hình trụ có bán kính đáy r, chiều cao h (Hình 6a) gồm hai hình tròn và một hình chữ nhật (Hình 6b). Diện tích của hình chữ nhật trong Hình 6b được gọi là diện tích xung quanh của hình trụ.
Hãy tính diện tích xung quanh của hình trụ theo r và h.
Đáp án và cách giải chi tiết:
Trong Hình 6b:
• Chiều dài hình chữ nhật bằng chu vi hình tròn và bằng 2πr (đvđd).
• Chiều rộng hình chữ nhật là h.
Diện tích xung quanh của hình trụ cũng là diện tích hình chữ nhật và bằng 2πrh (đvdt).
Vậy diện tích xung quanh của hình trụ là Sxq = 2πrh.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 84 Toán 9 Tập 2
Cuộn giấy in trong nhà máy, hộp sữa, hộp đựng quả cầu lông như hình bên có đặc điểm gì chung? Trong thực tế có đồ vật nào có hình dạng tương tự?

Khám phá 1 trang 84 Toán 9 Tập 2
Cho tấm bìa có dạng hình chữ nhật AA'O'O (Hình 1a). Khi quay tấm bìa một vòng quanh OO' cố định thì hình tạo ra giống với đồ vật quen thuộc nào?

Thực hành 1 trang 85 Toán 9 Tập 2
Quan sát và cho biết đường sinh, độ dài bán kính đáy và chiều cao của hình trụ trong Hình 4.

Thực hành 2 trang 85 Toán 9 Tập 2
Tạo lập chiếc hộp dạng hình trụ có chiều cao 10 cm, bán kính đáy 3 cm theo hướng dẫn sau:
Bước 1: Cắt một tấm bìa hình chữ nhật có cạnh 10 cm và cạnh 6π cm (≈ 19 cm) (Hình 5a).
Bước 2: Ghép hai cạnh 10 cm của tấm bìa lại với nhau sao cho hai cạnh 6π cm được uốn cong tạo thành hai đường tròn như Hình 5b.
Bước 3: Cắt hai tấm bìa hình tròn bán kính 3 cm rồi dán vào hai đường tròn vừa tạo thành ở Bước 2, ta được chiếc hộp như yêu cầu (Hình 5c).

Vận dụng trang 86 Toán 9 Tập 2
Một nhà máy dự định sản xuất thùng phuy đựng dầu nhớt dạng hình trụ có đường kính đáy 0,6 m và chiều cao 0,9 m (Hình 7). Bỏ qua diện tích các mép thùng, hãy tính diện tích thép cần để sản xuất 100 thùng phuy như vậy (kết quả làm tròn đến hàng phần trăm).

Khám phá 3 trang 86 Toán 9 Tập 2
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình.
a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B.
b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r và h.

Thực hành 3 trang 87 Toán 9 Tập 2
Phần bên trong của một cái bể hình trụ có chiều cao 2,1 m và bán kính đáy 1,5 m. Tính thể tích lượng nước trong bể biết mực nước bằng  chiều cao của bể (kết quả làm tròn đến hàng đơn vị).
chiều cao của bể (kết quả làm tròn đến hàng đơn vị).
Bài 2 trang 87 Toán 9 Tập 2
Tìm chiều cao, bán kính đáy và diện tích xung quanh, thể tích của mỗi hình trụ sau:

Bài 3 trang 87 Toán 9 Tập 2
Tạo lập hình trụ có bán kính đáy 4 cm, chiều cao 7 cm.
Bài 4 trang 87 Toán 9 Tập 2
Phần bên trong một chiếc thùng có dạng hình trụ với bán kính đáy 0,6 m, chiều cao 0,8 m. Người ta muốn sơn mặt bên trong hình trụ (bao gồm mặt đáy). Hỏi diện tích cần sơn là bao nhiêu (kết quả làm tròn đến hàng phần trăm).
Bài 5 trang 87 Toán 9 Tập 2
Một bể nước hình trụ có bán kính R = 1,2 m (tính từ tâm bể đến mép ngoài), bề dày của thành bể là b = 0,05 m, chiều cao lòng bể là h = 1,6 m (Hình 12). Tính dung tích của bể nước (kết quả làm tròn đến hàng phần trăm).