Giải bài tập Khám phá 1 trang 98 Toán 9 Tập 1 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Khám phá 1 trang 98 Toán 9 Tập 1. Bài 4. Hình quạt tròn và hình vành khuyên. Toán 9 - Chân trời sáng tạo
Đề bài:
Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau. Hãy tính:
a) Độ dài của toàn bộ hàng rào.
b) Độ dài của mỗi phần hàng rào.
c) Độ dài của n phần hàng rào.
Đáp án và cách giải chi tiết:
a) Độ dài củ toàn bộ hàng rào (chu vi của đường tròn) là: 2π.10 = 20π (m).
b) Độ dài của mỗi phần hàng rào là: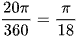 
(m).
c) Độ dài của n phần hàng rào là: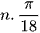 
(m).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 98 Toán 9 Tập 1
Số lượng cây ăn trái của trang trại Đất Lành được cho trong bảng sau:
Số liệu trên được biểu diễn trong biểu đồ hình quạt tròn bên.
Hình các phần được chia từ hình tròn trong biểu đồ bên gọi là gì? Làm thế nào để vẽ được chúng?
Thực hành 1 trang 99 Toán 9 Tập 1
Tính độ dài cung 72° của một đường tròn có bán kính 25 cm.
Vận dụng 1 trang 99 Toán 9 Tập 1
Tính độ dài của đoạn hàng rào từ A đến B của sân cỏ trong Hình 3, cho biết 
.
Khám phá 2 trang 99 Toán 9 Tập 1
a) Ta có thể tính diện tích của miếng bánh pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không?
b) Chia một hình tròn bán kính R thành 360 phần bằng nhau.
i) Tính diện tích của mỗi phần đó.
ii) Tính diện tích phần hình tròn ghép bởi n phần bằng nhau nói trên (Hình 4b).
Thực hành 2 trang 100 Toán 9 Tập 1
Tính diện tích hình quạt tròn bán kính R = 20 cm, ứng với cung 72°.
Vận dụng 2 trang 100 Toán 9 Tập 1
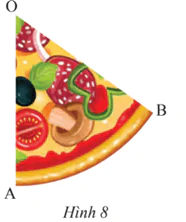
Tính diện tích của miếng bánh pizza có dạng hình quạt tròn trong Hình 8. Biết OA = 15 cm và 
.
Khám phá 3 trang 101 Toán 9 Tập 1
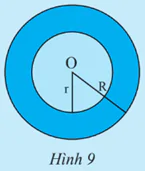
a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm.
b) Tính diện tích S của (C) và diện tích S’ của (C’).
c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.
Thực hành 3 trang 101 Toán 9 Tập 1
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) (kết quả làm tròn đến hàng phần trăm).
Vận dụng 3 trang 101 Toán 9 Tập 1
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11).
a) Tính độ dài đoạn thẳng BC theo r và R.
b) Cho BC = 
. Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a.
Bài 1 trang 102 Toán 9 Tập 1
Tính độ dài các cung 30°; 90°; 120° của đường tròn (O; 6 cm).
Bài 2 trang 102 Toán 9 Tập 1
Tính diện tích các hình quạt tròn ứng với cung có số đo lần lượt là 30°; 90°; 120° của hình tròn (O; 12 cm).
Bài 3 trang 102 Toán 9 Tập 1
Tính diện tích các hình quạt tròn ứng với cung có độ dài lần lượt là 8 cm, 15 cm của hình tròn (O; 5 cm).
Bài 4 trang 102 Toán 9 Tập 1
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 9 cm) và (O; 12 cm).
Bài 5 trang 102 Toán 9 Tập 1
Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung có số đo là 95° (Hình 12).
Bài 6 trang 102 Toán 9 Tập 1
Một máy kéo nông nghiệp có đường kính bánh xe sau là 124 cm và đường kính bánh xe trước là 80 cm. Hỏi khi bánh xe sau lăn được 20 vòng thì bánh xe trước lăn được bao nhiêu vòng?
Bài 7 trang 102 Toán 9 Tập 1
Thành phố Đà Lạt nằm vào khoảng 11°58’ vĩ độ Bắc. Mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000 km. Hãy tính độ dài cung kinh tuyến từ Đà Lạt đến xích đạo.
