Giải bài tập Hoạt động 2: Vẽ đường tròn bằng phần mềm GeoGebra | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động 2: Vẽ đường tròn bằng phần mềm GeoGebra. Hoạt động 2. Vẽ đường tròn bằng phần mềm GeoGebra. Toán 9 - Chân trời sáng tạo
Đề bài:

Mục tiêu:
− Thực hành sử dụng phần mềm Geogebra để vẽ các đường tròn.
− Xem xét sự thay đổi của diện tích hình tròn khi thay đổi bán kính.
− Ôn tập và minh họa các tính chất đã học về đường tròn.
− Thực hành sử dụng phần mềm để thiết kế đồ họa liên quan đến đường tròn.
Chuẩn bị:
− Máy tính xách tay hoặc máy tính bảng có cài đặt Geogebra hoặc có kết nối Internet.
− Máy chiếu hoặc màn hình ti vi lớn.
− Thực hành trong phòng máy nếu các trường có điều kiện.
− Sách giáo khoa Toán 9, tập một – Chân trời sáng tạo.
Hướng dẫn chức năng của Geogebra:
Để vẽ đường tròn trên Geogebra ta thực hiện các thao tác trên hai vùng sau:
1. Vùng chứa các thanh công cụ;
2. Vùng vẽ hình: chứa các đường tròn vẽ được.

Đáp án và cách giải chi tiết:
Hoạt động 1. Vẽ đường tròn theo các cách khác nhau
Để vẽ đường tròn trên Geogebra, ta có các cách sau:
Cách 1. Vẽ đường tròn khi biết tâm và một điểm trên đường tròn.
1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online.
2. Các bước thao tác trên Geogebra:
− Chọn thẻ điểm trên thanh công cụ.
− Nhấp chuột vào hai điểm tùy ý trên vùng vẽ hình.
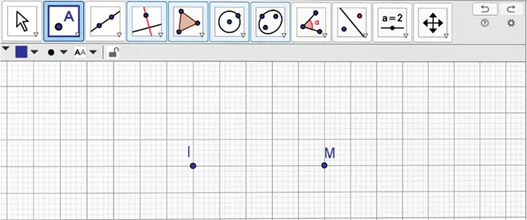
− Phần mềm sẽ tự động đặt tên điểm, tuy nhiên ta có thể đổi tên điểm bằng cách nhấp chuột phải vào điểm, chọn đổi tên và gõ tên mới vào hộp thoại.

− Chọn thẻ vẽ đường tròn trên thanh công cụ. Tiếp tục chọn “Đường tròn khi biết tâm và 1 điểm trên đường tròn”.
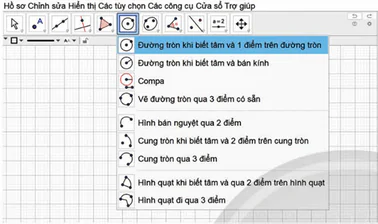
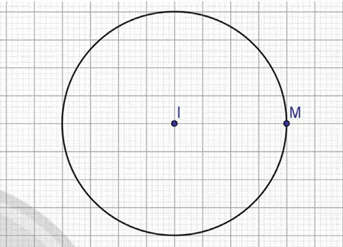
− Nhấp chuột vào hai điểm I và điểm M. Phần mềm sẽ tự động vẽ đường tròn tâm I bán kính IM.
Cách 2. Vẽ đường tròn khi biết tâm và số đo của bán kính.
1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online.
2. Các bước thao tác trên Geogebra:
− Vẽ trước tâm O và tạo thanh trượt biểu thị tham số r.
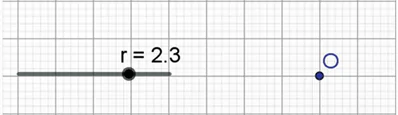
− Chọn thẻ vẽ đường tròn trên thanh công cụ. Tiếp tục chọn “Đường tròn khi biết tâm và bán kính”.
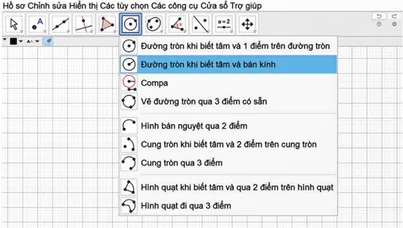
− Nhấp chuột vào điểm O và nhập bán kính bằng r vào hộp thoại hiện ra.
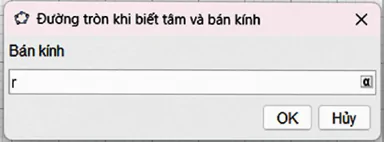
− Phần mềm tự động vẽ đường tròn (O; r).
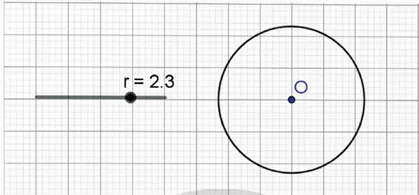
− Dùng chuột thay đổi r để thay đổi bán kính.
Tương tự như cách 1 và cách 2, ta có thể vẽ đường tròn theo các cách sau:
Cách 3. Vẽ đường tròn khi biết tâm và một đoạn thẳng có độ dài bằng bán kính (chế độ Compa).
Thao tác trên phần mềm GeoGebra được thực hiện như sau:
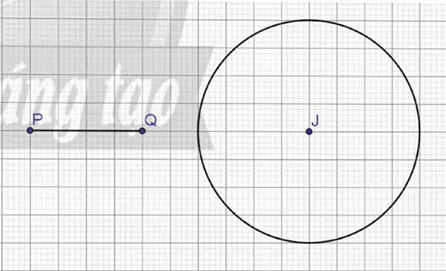
− Vẽ trước tâm J và một đoạn thẳng PQ.
− Chọn thẻ vẽ đường tròn trên thanh công cụ. Tiếp tục chọn “Compa”.
− Nhấp chuột vào tâm J, sau đó nhấp chuột vào đoạn thẳng PQ.
− Ta có đường tròn tâm J bán kính r = PQ.
Cách 4. Vẽ đường tròn đi qua ba điểm. Thao tác trên phần mềm GeoGebra được thực hiện như sau:
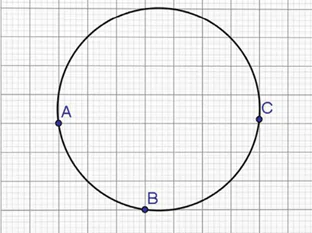
− Vẽ trước ba điểm A, B, C không thẳng hàng.
− Chọn thẻ vẽ đường tròn trên thanh công cụ. Tiếp tục chọn “Vẽ đường tròn qua 3 điểm có sẵn”.
− Nhấp chuột lần lượt vào ba điểm A, B, C.
− Ta có đường tròn đi qua ba điểm A, B, C như hình bên.
Hoạt động 2. Tính diện tích hình tròn
Tính diện tích của hình tròn tâm O bán kính r.
1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online.
2. Các bước thao tác trên Geogebra:
− Vẽ đường tròn tâm O bán kính r theo Cách 2.
− Chọn chức năng đo diện tích 
− Nhấp chuột vào đường tròn tâm O bán kính r.
− Ta có diện tích hình tròn vừa vẽ (theo cm2) như hình dưới đây.
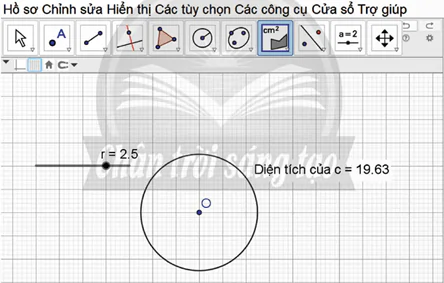
− Dùng chuột kéo con chạy để thay đổi bán kính r. Quan sát diện tích hình tròn thay đổi khi thay đổi bán kính r.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Thực hành 1
a) Vẽ đường tròn tâm O bán kính r = 5 theo Cách 2.
b) Vẽ tam giác MNP rồi vẽ đường tròn ngoại tiếp theo Cách 4.
Thực hành 2
a) Vẽ đường tròn tâm J bán kính r = 4 theo Cách 2 và tính diện tích hình tròn vừa vẽ được.
b) Vẽ điểm O, đoạn thẳng AB và đường tròn O bán kính bằng AB theo Cách 3. Tính diện tích hình tròn vừa vẽ được.