Giải bài tập Bài 3 trang 21 Toán 9 Tập 1 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 21 Toán 9 Tập 1. Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn.. Toán 9 - Chân trời sáng tạo
Đề bài:
Bài 3 trang 21 Toán 9 Tập 1: Xác định a, b để đồ thị hàm số 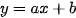 đi qua hai điểm A và B trong mỗi trường hợp sau
đi qua hai điểm A và B trong mỗi trường hợp sau
a)  và
và  ;
;
b) 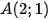 và
và 
Đáp án và cách giải chi tiết:
a) • Đồ thị hàm số 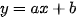 đi qua hai điểm
đi qua hai điểm 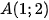 nên
nên
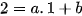 hay
hay 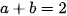 . (1)
. (1)
• Đồ thị hàm số 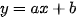 đi qua hai điểm
đi qua hai điểm 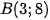 nên
nên
8 = a . 3 + b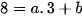 hay
hay 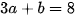 . (2)
. (2)
Từ (1) và (2) ta có hệ phương trình 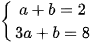 (I)
(I)
Trừ từng vế hai phương trình của hệ (I), ta được 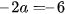 . Suy ra
. Suy ra 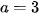 .
.
Thay 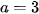 vào phương trình thứ nhất của hệ (I), ta được
vào phương trình thứ nhất của hệ (I), ta được 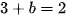 . Do đó
. Do đó 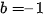 .
.
Vậy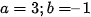 .
.
b) • Đồ thị hàm số  đi qua hai điểm
đi qua hai điểm 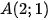 nên
nên
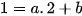 hay
hay 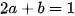 . (1)
. (1)
• Đồ thị hàm số 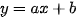 đi qua hai điểm
đi qua hai điểm 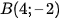 nên
nên
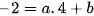 hay
hay 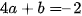 . (2)
. (2)
Từ (1) và (2) ta có hệ phương trình 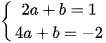 (I)
(I)
Trừ từng vế hai phương trình của hệ (I), ta được 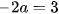 . Suy ra
. Suy ra 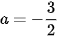 .
.
Thay 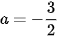 vào phương trình thứ nhất của hệ (I), ta được
vào phương trình thứ nhất của hệ (I), ta được 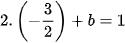 hay
hay 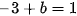 . Do đó
. Do đó 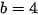 .
.
Vậy 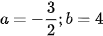 .
.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 21 Toán 9 Tập 1
Bài 1 trang 21 Toán 9 Tập 1: Giải các hệ phương trình:
a)  ;
;
b)  ;
;
c)  ;
;
d) 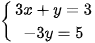 .
.
Bài 2 trang 21 Toán 9 Tập 1
Bài 2 trang 21 Toán 9 Tập 1: Giải các hệ phương trình:
a) 
b) 
c) 
d)  .
.
Bài 4 trang 21 Toán 9 Tập 1
Bài 4 trang 21 Toán 9 Tập 1: Trong tháng thứ nhất, hai tổ sản xuất được 800 chi tiết máy. So với tháng thứ nhất, trong tháng thứ hai, tổ một sản xuất vược 15%, tổ hai sản xuất vượt 20% nên trong tháng này, cả hai tổ đã sản xuất được 945 chi tiết máy. Hỏi trong tháng thứ nhất mỗi tổ sản xuất được bao nhiêu chi tiết máy?
Bài 5 trang 21 Toán 9 Tập 1
Bài 5 trang 21 Toán 9 Tập 1: Hai tổ sản xuất cùng may một loại áo khoác xuất khẩu. Nếu tổ thứ nhất may trong 7 ngày và tổ thứ hai may trong 5 ngày thì cả hai tổ may được 1540 chiếc áo. Biết rằng mỗi ngày tổ thứ hai may được nhiều hơn tổ thứ nhất 20 chiếc áo. Hỏi trong một ngày mỗi tổ may được bao nhiêu chiếc áo? (Năng suất may áo của mỗi tổ trong các ngày là như nhau.)
Bài 6 trang 21 Toán 9 Tập 1
Bài 6 trang 21 Toán 9 Tập 1: Trên một cánh đồng, người ta cấy 60 ha lúa giống mới và 40 ha lúa giống cũ, thu hoạch được tất cả 660 tấn thóc. Hỏi năng suất lúa giống mới trên 1 ha bằng bao nhiêu? Biết rằng 3 ha trồng lúa giống mới thu hoạch được ít hơn 4 ha trồng lúa giống cũ là 3 tấn.
Bài 7 trang 21 Toán 9 Tập 1
Bài 7 trang 21 Toán 9 Tập 1: Cân bằng các phương trình hóa học sau bằng phương pháp đại số
a) Ag + Cl2 → AgCl
b) CO2 + C → CO
Khởi động trang 15 Toán 9 Tập 1
Tại một cửa hàng, chị An mua 1,2 kg thịt lợn và 0,7 kg thịt bò hết 362 000 đồng; chị Ba mua 0,8 kg thịt lợn và 0,5 kg thịt bò cùng loại hết 250 000 đồng. Làm thế nào để tính được giá tiền 1 kg mỗi loại thịt lợn và thịt bò?
Khám phá 1 trang 15 Toán 9 Tập 1
Cho hệ phương trình 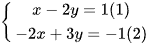
Thực hiện giải hệ phương trình này theo hướng dẫn sau:
– Từ phương trình (1), hãy biểu diễn x theo y.
– Thế x được biểu diễn ở trên vào phương trình (2), để nhận được một phương trình ẩn y.
– Giải phương trình ẩn y đó, rồi suy ra nghiệm của hệ.
Khám phá 2 trang 17 Toán 9 Tập 1
Cho hệ hai phương trình  và
và 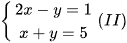 .
.
a) Giải hệ phương trình (I) và hệ phương trình (II) bằng phương pháp thế. Có nhận xét gì về nghiệm của hai hệ này?
b) Bằng cách cộng từng vế hai phương trình của hệ (II), ta nhận được một phương trình mới. Thay phương trình thứ nhất của hệ (II) bằng phương trình mới đó. Có nhận xét gì về kết quả nhận được?
Vận dụng 1 trang 18 Toán 9 Tập 1
Xác định a, b để đồ thị hàm số y = ax + b đi qua hai điểm A(2; –2) và B(–1; 3).
Thực hành 3 trang 19 Toán 9 Tập 1
Tìm nghiệm của các hệ phương trình sau bằng máy tính cầm tay:
a)  ;
;
b) 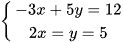 .
.
Khám phá 3 trang 19 Toán 9 Tập 1
Hai lớp 9A và 9B có tổng số 82 học sinh. Trong dịp tết trồng cây năm 2022, mỗi học sinh lớp 9A trồng được 3 cây, mỗi học sinh lớp 9B trồng được 4 cây nên cả hai lớp trồng được tổng số 288 cây. Gọi x, y lần lượt là số học sinh lớp 9A và lớp 9B  .
.
a) Từ dữ liệu đã cho, lập hai phương trình bậc nhất hai ẩn biểu thị số học sinh của hai lớp và số cây trồng được.
b) Giải hệ hai phương trình bậc nhất hai ẩn và cho biết mỗi lớp bao nhiêu học sinh.
Thực hành 4 trang 20 Toán 9 Tập 1
Một mảnh vườn hình chữ nhật có chu vi 64 m. Nếu tăng chiều dài thêm 2 m và tăng chiều rộng thêm 3 m thì diện tích tăng thêm 88 m2. Tính chiều dài, chiều rộng của mảnh vườn đó.
Thực hành 5 trang 20 Toán 9 Tập 1
Cân bằng phương trình hóa học sau bằng phương pháp đại số.
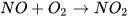
Vận dụng 2 trang 20 Toán 9 Tập 1
Giải bài toán trong Hoạt động khởi động (trang 15).
 ;
;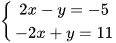 ;
; .
. ;
;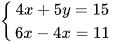 .
.