Giải bài tập Bài 9.35 trang 109 Toán 8 Tập 2 | Toán 8 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 9.35 trang 109 Toán 8 Tập 2. Luyện tập chung chương 9 trang 108.. Toán 8 - Kết nối tri thức
Đề bài:
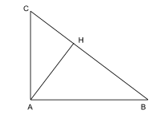
Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ΔHBM∽ ΔHAN.
Đáp án và cách giải chi tiết:
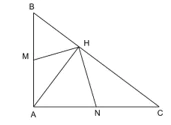
Ta có: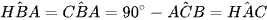 
(tam giác ABC vuông tại A và tam giác HAC vuông tại H).
Xét hai tam giác HBA vuông tại H và tam giác HAC vuông tại H có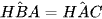 
(chứng minh trên) nên ∆HBA ∽ ∆HAC.
Suy ra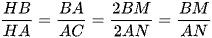 
(Vì M, N là trung điểm của AB và AC).
Xét tam giác HBM và tam giác HAN có
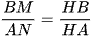(chứng minh trên)
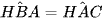hay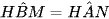 
Do đó ∆HBM ∽ ∆HAN (c.g.c).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 9.32 trang 109 Toán 8 Tập 2
Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.
a) Tính độ dài đoạn thẳng AH.
b) Tính độ dài các đoạn thẳng AB và AC.
Bài 9.33 trang 109 Toán 8 Tập 2
Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P.
a) Chứng minh rằng ΔBMP ∽ ΔMCN.
b) Tính độ dài đoạn thẳng AM.
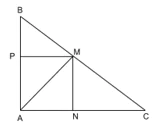
Bài 9.34 trang 109 Toán 8 Tập 2
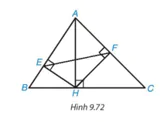
Trong Hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng:
a) ΔAEH ∽ ΔAHB;
b) ΔAFH ∽ ΔAHC;
c) ΔAFE ∽ ΔABC.
Bài 9.36 trang 109 Toán 8 Tập 2
Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m.
a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?
b) Vào buổi chiều khi bóng bạn An dài 3 m, hỏi bóng cột cờ dài bao nhiêu mét?