Giải bài tập Bài 1.2 trang 10 Toán 9 Tập 1 | Toán 9 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 1.2 trang 10 Toán 9 Tập 1. Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn.. Toán 9 - Kết nối tri thức
Đề bài:
a) Tìm giá trị thích hợp thay cho dấu "?" trong bảng sau rồi cho biết 6 nghiệm của phương trình 2x – y = 1:
| x | -1 | -0,5 | 0 | 0,5 | 1 | 2 |
| y = 2x – 1 | ? | ? | ? | ? | ? | ? |
b) Viết nghiệm tổng quát của phương trình đã cho.
Đáp án và cách giải chi tiết:
a)
• Với x = –1, ta có y = 2 . (–1) – 1 = – 2 – 1 = –3;
• Với x = –0,5, ta có y = 2 . (–0,5) – 1 = – 1 – 1 = –2;
• Với x = 0, ta có y = 2 . 0 – 1 = 0 – 1 = –1;
• Với x = 0,5, ta có y = 2 . 0,5 – 1 = 1 – 1 = 0;
• Với x = 1, ta có y = 2 . 1 – 1 = 2 – 1 = 1;
• Với x = 2, ta có y = 2 . 2 – 1 = 4 – 1 = 3.
Vậy ta có bảng sau:
| x | –1 | –0,5 | 0 | 0,5 | 1 | 2 |
| y = 2x – 1 | -3 | -2 | -1 | 0 | 1 | 3 |
Vậy 6 nghiệm của phương trình đã cho là (–1; –3), (–0,5; –2), (0; –1), (0,5; 1), (1; 1), (2; 3).
b) Ta có y = 2x – 1. Với mỗi giá trị x tùy ý cho trước, ta luôn tìm được một giá trị y tương ứng.
Do đó, phương trình đã cho có vô số nghiệm.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Mở đầu trang 5 Toán 9 Tập 1
Xét bài toán cổ sau:
Quýt, cam mười bảy quả tươi
Đem chia cho một trăm người cùng vui.
Chia ba mỗi quả quýt rồi,
Còn cam, mỗi quả chia mười vừa xinh.
Trăm người, trăm miếng ngon lành.
Quýt, cam mỗi loại tính rành là bao?

Trong bài toán này có hai đại lượng chưa biết (số cam và số quýt). Vậy ta có thể giải bài toán đó tương tự “giải bài toán bằng cách lập phương trình” được hay không? Để trả lời câu hỏi này, trước hết chúng ta cần tìm hiểu về phương trình và hệ hai phương trình bậc nhất hai ẩn.
HĐ1 trang 6 Toán 9 Tập 1
Câu “Quýt, cam mười bảy quả tươi” có nghĩa là tổng số cam và số quýt là 17. Hãy viết hệ thức với hai biến x và y biểu thị giả thiết này.
HĐ2 trang 6 Toán 9 Tập 1
Tương tự, hãy viết hệ thức hai biến x và y biểu thị giả thiết cho bởi các câu thơ thứ ba, thứ tư và thứ năm.
Luyện tập 1 trang 6 Toán 9 Tập 1
Hãy viết một phương trình bậc nhất hai ẩn và chỉ ra một nghiệm của nó.
Luyện tập 2 trang 8 Toán 9 Tập 1
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:
a) 2x – 3y = 5;
b) 0x + y = 3;
c) x + 0y = −2.
Luyện tập 3 trang 9 Toán 9 Tập 1
Trong hai cặp số (0; −2); và (2; −1), cặp số nào là nghiệm của hệ phương trình 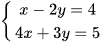 ?
?
Vận dụng trang 9, 10 Toán 9 Tập 1
Xét bài toán cổ trong tình huống mở đầu. Gọi x là số cam, y là số quýt cần tính (x, y ∈ ℕ*), ta có hệ phương trình bậc nhất hai ẩn sau: 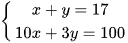 .
.
Trong hai cặp số (10; 7) và (7; 10), cặp số nào là nghiệm của hệ phương trình trên? Từ đó cho biết một phương án về số cam và số quýt thỏa mãn yêu cầu của bài toán cổ.
Bài 1.1 trang 10 Toán 9 Tập 1
Phương trình nào sau đây là phương trình bậc nhất hai ẩn? Vì sao?
a) 5x – 8y = 0;
b) 4x + 0y = –2;
c) 0x + 0y = 1;
d) 0x – 3y = 9.
Bài 1.3 trang 10 Toán 9 Tập 1
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:
a) 2x – y = 3;
b) 0x + 2y = –4;
c) 3x + 0y = 5.
Bài 1.4 trang 10 Toán 9 Tập 1
Cho hệ phương trình 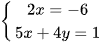 .
.
a) Hệ phương trình trên có là một hệ hai phương trình bậc nhất hai ẩn không? Vì sao?
b) Cặp số (–3; 4) có là một nghiệm của hệ phương trình đã cho hay không? Vì sao?
Bài 1.5 trang 10 Toán 9 Tập 1
Cho các cặp số (–2; 1), (0; 2), (1; 0), (1,5; 3), (4; –3) và hai phương trình
5x + 4y = 8, (1)
3x + 5y = –3. (2)
Trong các cặp số đã cho:
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?
c) Vẽ hai đường thẳng 5x + 4y = 8 và 3x + 5y = –3 trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.