Giải bài tập Vận dụng 1 trang 44 Toán 8 Tập 1 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Vận dụng 1 trang 44 Toán 8 Tập 1. Bài 1. Hình chóp tam giác đều – Hình chóp tứ giác đều. Toán 8 - Chân trời sáng tạo
Đề bài:
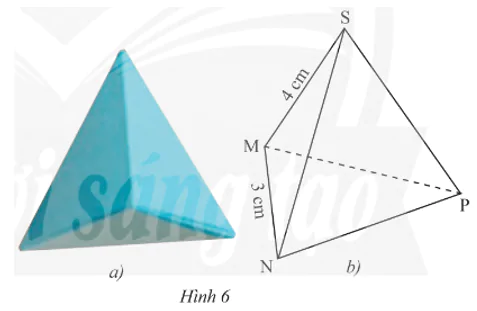
Chiếc hộp (Hình 6a) được vẽ lại như Hình 6b có dạng hình chóp tam giác đều S.MNP.
a) Hãy cho biết mặt đáy, mặt bên, cạnh bên của chiếc hộp đó.
b) Cho biết SM = 4 cm, MN = 3 cm. Tìm độ dài các cạnh còn lại của chiếc hộp.
c) Mỗi góc của tam giác đáy MNP bằng bao nhiêu độ?
Đáp án và cách giải chi tiết:
a) Chiếc hộp dạng hình chóp tam giác đều S.MNP ở Hình 6 có:
• Mặt đáy: MNP;
• Các mặt bên: SMN, SNP, SPM;
• Các cạnh bên: SM, SN, SP.
b) Xét chiếc hộp dạng hình chóp tam giác đều S.MNP có:
• SN = SP = SM = 4 cm;
• NP = PQ = MN = 3 cm.
c) Tam giác đáy MNP là tam giác đều nên mỗi góc của tam giác này bằng  .
.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 43 Toán 8 Tập 1
Hãy cho biết các mặt bên của kim tự tháp và khối rubik ở bên dưới là các hình gì.

Khám phá 1 trang 43 Toán 8 Tập 1
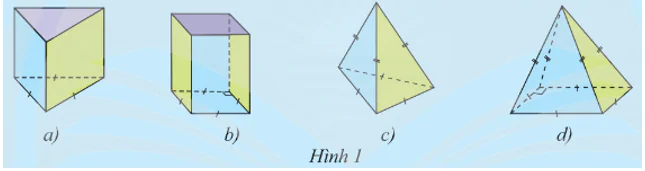
Quan sát các hình không gian trong Hình 1 và trả lời các câu hỏi sau:
a) Các mặt bên của mỗi hình là hình gì?
b) Hình nào có các cạnh bên bằng nhau và đáy là hình tam giác đều?
c) Hình nào có các cạnh bên bằng nhau và đáy là hình vuông?
Thực hành 1 trang 43 Toán 8 Tập 1
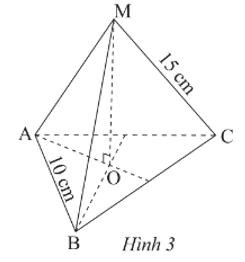
Hãy cho biết mặt bên, mặt đáy, đường cao, độ dài cạnh bên, độ dài cạnh đáy của hình chóp tam giác đều ở Hình 3.
Thực hành 2 trang 44 Toán 8 Tập 1
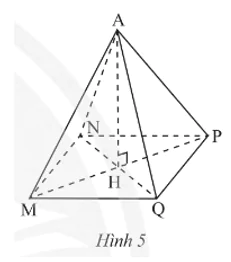
Cho hình chóp tứ giác đều A.MNPQ (Hình 5).
a) Hãy cho biết đỉnh, cạnh bên, mặt bên, cạnh đáy, mặt đáy, đường cao của hình chóp tứ giác đều đó.
b) Cho biết AM = 5 cm, MN = 4 cm. Tìm độ dài các cạnh AN, AP, AQ, NP, PQ, QM.
Thực hành 3 trang 44 Toán 8 Tập 1
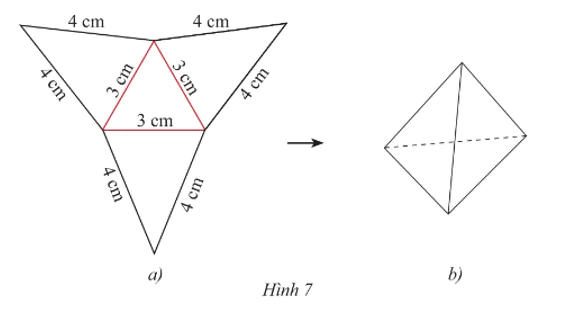
Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3 cm và cạnh bên 4 cm theo hướng dẫn sau:
‒ Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.
‒ Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.
Vận dụng 2 trang 45 Toán 8 Tập 1
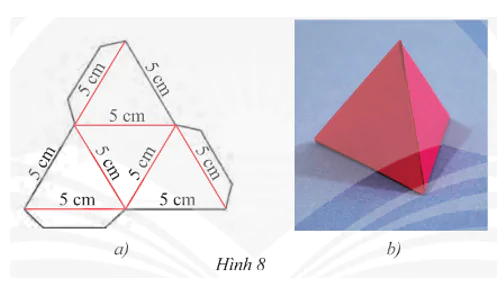
Cắt, gấp và dán hộp quà hình chóp tam giác đều có độ dài cạnh đáy và cạnh bên bằng 5 cm.
Gợi ý: Cắt theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.
Thực hành 4 trang 45 Toán 8 Tập 1
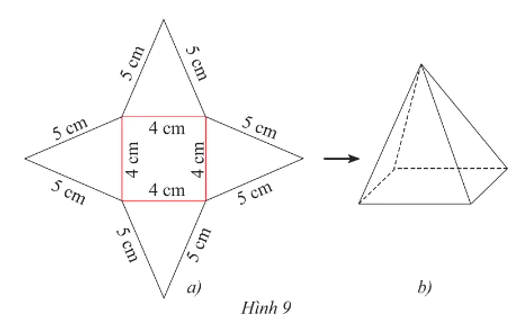
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4 cm và cạnh bên 5 cm theo hướng dẫn sau:
‒ Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.
‒ Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
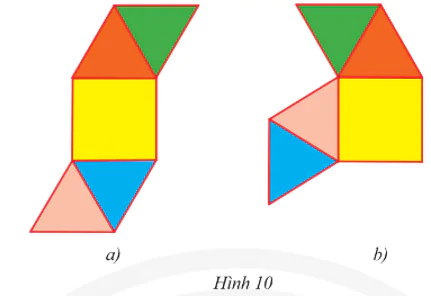
Vận dụng 3 trang 46 Toán 8 Tập 1
Tấm bìa nào sau đây có thể gấp thành hình chóp tứ giác đều?
Bài 1 trang 46 Toán 8 Tập 1
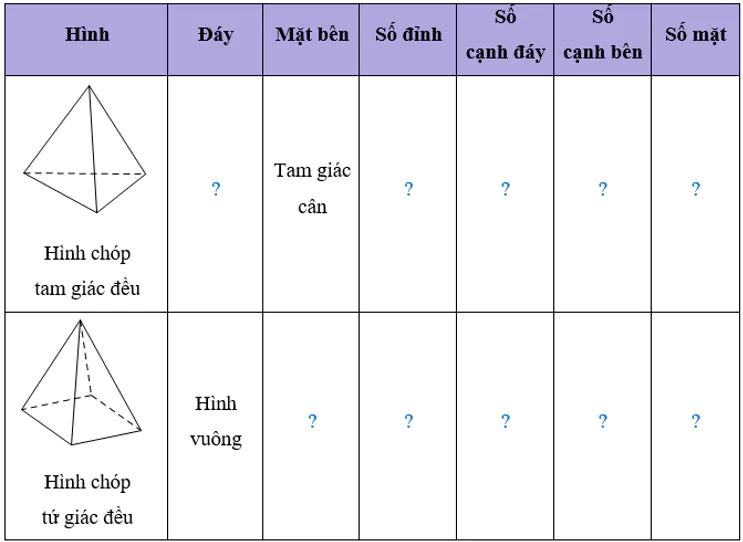
Quan sát hai hình dưới đây và thay mỗi dấu ? cho thích hợp.
Bài 2 trang 46 Toán 8 Tập 1
Cho hình chóp tứ giác đều S.MNPQ có cạnh bên SM = 15 cm và cạnh đáy MN = 8 cm. Hãy cho biết:
a) Mặt bên và mặt đáy của hình đó.
b) Độ dài các cạnh bên và cạnh đáy còn lại của hình đó.
Bài 3 trang 47 Toán 8 Tập 1
Cho hình chóp tam giác đều S.DEF có cạnh bên SE = 5 cm và cạnh đáy EF = 3 cm. Hãy cho biết:
a) Mặt bên và mặt đáy của hình chóp.
b) Độ dài các cạnh bên và cạnh đáy còn lại của hình chóp.
c) Số đo mỗi góc của mặt đáy.
Bài 4 trang 47 Toán 8 Tập 1
Các phát biểu sau đúng hay sai? Nếu sai thì sửa lại cho đúng.
a) Hình chóp tam giác đều có các cạnh bên bằng nhau và đáy là hình tam giác có ba cạnh bằng nhau.
b) Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.
Bài 5 trang 47 Toán 8 Tập 1
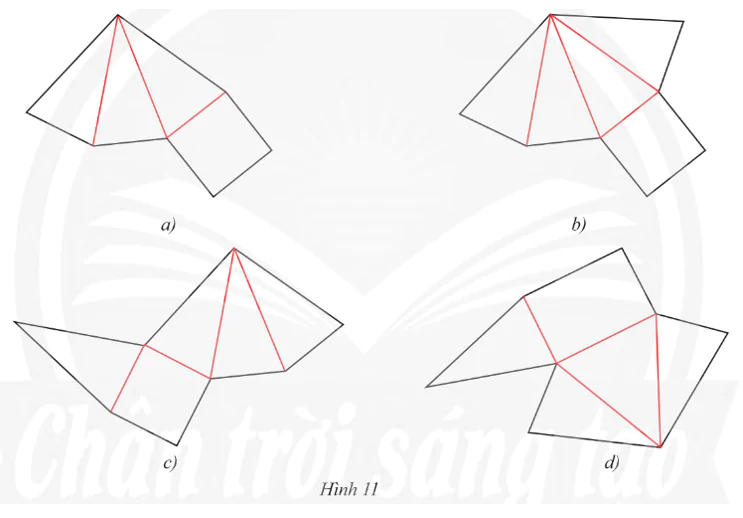
Trong các tấm bìa dưới đây, tấm bìa nào gấp theo đường màu đỏ thì được một hình chóp tứ giác đều?
Bài 6 trang 47 Toán 8 Tập 1
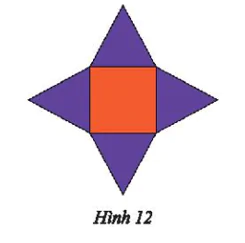
Chị Hà dự định gấp một hộp quà từ tấm bìa như Hình 12. Cái hộp mà chị Hà dự định gấp có dạng hình gì?