Giải bài tập Toán 8 Hoạt động 4. Vẽ đồ thị hàm số bậc nhất y = ax + b bằng phần mềm GeoGebra. | Chân trời sáng tạo
Hướng dẫn giải chi tiết Hoạt động 4. Vẽ đồ thị hàm số bậc nhất y = ax + b bằng phần mềm GeoGebra.
HOẠT ĐỘNG 1: Vẽ đồ thị hàm số y = ax + b với a, b nhập từ bàn phím
HOẠT ĐỘNG 1: Vẽ đồ thị hàm số y = ax + b với a, b nhập từ bàn phím
Ví dụ: Vẽ đồ thị hàm số y = 2x + 4.
Thực hành 1 trang 98 Sách giáo khoa Toán 8 Tập 2
Vẽ đồ thị các hàm số bậc nhất sau:
a) y = −x – 2;
b) y = x – 2;
c)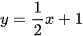 
;
d) y = −4x + 7.
HOẠT ĐỘNG 2: Vẽ đường thẳng ∆: y = ax + b với a, b thay đổi bằng thanh trượt
HOẠT ĐỘNG 2: Vẽ đường thẳng ∆: y = ax + b với a, b thay đổi bằng thanh trượt
1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phần mềm online.
2. Các bước thao tác trên GeoGebra:
- Tạo các thanh trượt biểu thị các tham số a, bằng cách nhấp chuột liên tiếp vào thanh công cụ 
và vào vị trí màn hình nơi ta muốn đặt thanh trượt.
- Nhập công thức đường thẳng tại vùng nhập lệnh theo cú pháp: y = ax + b.
- Quan sát đồ thị được vẽ trên cùng làm việc:
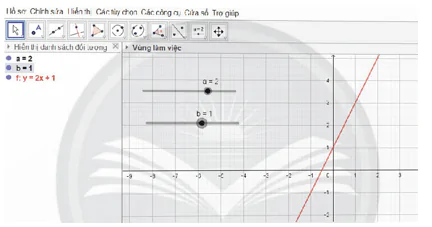
- Điều chỉnh các thanh trượt a, b để có giá trị mong muốn.
- Quan sát sự thay đổi của ∆ theo sự thay đổi các hệ số a, b.
- Chụp màn hình để có kết quả làm báo cáo, thu hoạch, trình chiếu.
3. Nêu các kết luận về tính chất của đồ thị quan sát được trên hình vẽ.
Thực hành 2 trang 98 Sách giáo khoa Toán 8 Tập 2
- Vẽ đường thẳng y = ax + b với a, b thay đổi bằng thanh trượt.
- Điều chỉnh a, b để vẽ được nhiều đường thẳng khác nhau.
- Giữ nguyên a chỉ điều chỉnh b để kiểm tra tính chất: các đường thẳng có cùng hệ số góc thì song song.