Giải bài tập Luyện tập 4 trang 26 Toán 12 Tập 1 | SGK Toán 12 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 4 trang 26 Toán 12 Tập 1. Bài 3. Đường tiệm cận của đồ thị hàm số.. SGK Toán 12 - Cánh diều
Đề bài:
Luyện tập 4 trang 26 Toán 12 Tập 1: Tìm tiệm cận xiên của đồ thị hàm số 
Đáp án và cách giải chi tiết:
Ta có: 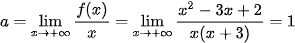
và 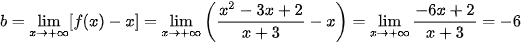
Vậy đường thẳng y = x – 6 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → + ∞).
Tương tự, do 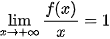 và
và 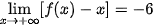 nên đường thẳng y = x – 6 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → – ∞).
nên đường thẳng y = x – 6 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → – ∞).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 27 Toán 12 Tập 1
Bài 1 trang 27 Toán 12 Tập 1: Tiệm cận đứng của đồ thị hàm số là:
A. .
B. .
C. .
D. .
Bài 2 trang 27 Toán 12 Tập 1
Bài 2 trang 27 Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số là:
A..
B. .
C. .
D..
Bài 3 trang 27 Toán 12 Tập 1
Bài 3 trang 27 Toán 12 Tập 1: Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?

Bài 5 trang 27 Toán 12 Tập 1:
Bài 5 trang 27 Toán 12 Tập 1: Số lượng sản phẩm bán được của một công ty trong x (tháng) được tính theo công thức , trong đó x ≥ 1 (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
a) Xem là một hàm số xác định trên nửa khoảng [1; + ∞), hãy tìm tiệm cận ngang của đồ thị hàm số đó.
b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.
Bài 4 trang 27 Toán 12 Tập 1
Bài 4 trang 27 Toán 12 Tập 1: Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:
a)  ;
;
b)  ;
;
c) 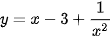 .
.
Câu hỏi khởi động trang 21 Toán 12 Tập 1
Câu hỏi khởi động trang 21 Toán 12 Tập 1: Số dân của một thị trấn sau x năm kể từ năm 1970 được ước tính bởi công thức 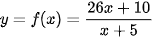 (f(x) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020). Xem y = f(x) là một hàm số xác định trên nửa khoảng [0; + ∞), đồ thị của hàm số đó là đường cong màu xanh ở Hình 10.
(f(x) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020). Xem y = f(x) là một hàm số xác định trên nửa khoảng [0; + ∞), đồ thị của hàm số đó là đường cong màu xanh ở Hình 10.
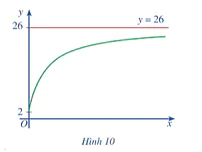
Khi  , đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng nào?
, đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng nào?
Luyện tập 1 trang 22 Toán 12 Tập 1
Luyện tập 1 trang 22 Toán 12 Tập 1: Tìm tiệm cận ngang của đồ thị hàm số 
Hoạt động 2 trang 22 Toán 12 Tập 1
Hoạt động 2 trang 22 Toán 12 Tập 1: Cho hàm số y = f(x) = có đồ thị là đường cong như Hình 12

Tìm 
Hoạt động 1 trang 21 Toán 12 Tập 1
Hoạt động 1 trang 21 Toán 12 Tập 1: Xét hàm số  , với
, với  có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm
có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm 

Luyện tập 2 trang 23 Toán 12 Tập 1
Luyện tập 2 trang 23 Toán 12 Tập 1: Tìm tiệm cận đứng của đồ thị hàm số 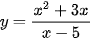
Hoạt động 3 trang 24 Toán 12 Tập 1
Hoạt động 3 trang 24 Toán 12 Tập 1: Cho hàm số  có đồ thị là (C) và đường thẳng y = x + 1 (Hình 15)
có đồ thị là (C) và đường thẳng y = x + 1 (Hình 15)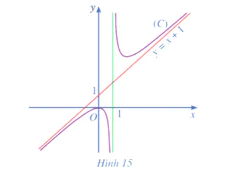
Tìm 
Luyện tập 3 trang 25 Toán 12 Tập 1
Luyện tập 3 trang 25 Toán 12 Tập 1: Chứng minh rằng đường thẳng y = – x là tiệm cận xiên của đồ thị hàm số  .
.