Giải bài tập HĐ1 trang 53 Toán 8 Tập 1 | Toán 8 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập HĐ1 trang 53 Toán 8 Tập 1. Bài 11. Hình thang cân. Toán 8 - Kết nối tri thức
Đề bài:
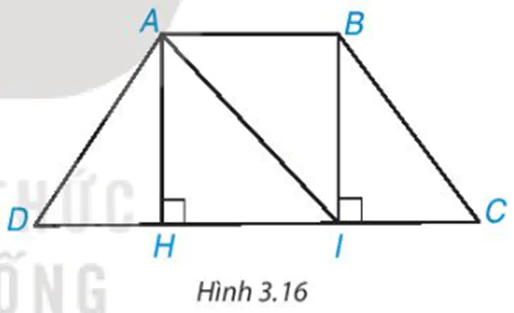
Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16).
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.
Đáp án và cách giải chi tiết:
a) Vì ABCD là hình thang cân (AB // CD) nên (hai góc so le trong).
Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.
Do đó (hai góc so le trong).
Xét ∆AHI và ∆IBA có:
(chứng minh trên);
Cạnh AI chung;
(hai góc so le trong).
Do đó ∆AHI = ∆IBA (c.g.c).
Suy ra AH = BI (hai cạnh tương ứng).
b) Vì ABCD là hình thang cân (AB // CD) nên (1).
Xét ∆AHD vuông tại H có (2) (trong tam giác vuông, hai góc nhọn có tổng số đo bằng 90°).
Tương tự, ∆BIC vuông tại I có (3).
Từ (1), (2) và (3) suy ra .
Xét ∆AHD và ∆BIC có:
(vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);
AH = BI (chứng minh câu a);
(chứng minh trên).
Do đó ∆AHD = ∆BIC (cạnh góc vuông – góc nhọn kề).
Suy ra AD = BC (hai cạnh tương ứng).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Mở đầu trang 52 Toán 8 Tập 1
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.

Luyện tập 1 trang 53 Toán 8 Tập 1
Tính các góc của hình thang cân ABCD (AB // CD), biết (H.3.15).

Luyện tập 2 trang 53 Toán 8 Tập 1
Cho tứ giác ABCD như Hình 3.18. Biết rằng . Chứng minh rằng AD = BC.

HĐ2 trang 54 Toán 8 Tập 1
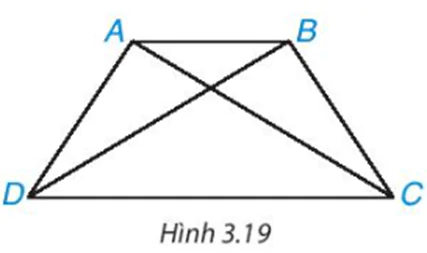
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD.
Luyện tập 3 trang 54 Toán 8 Tập 1
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
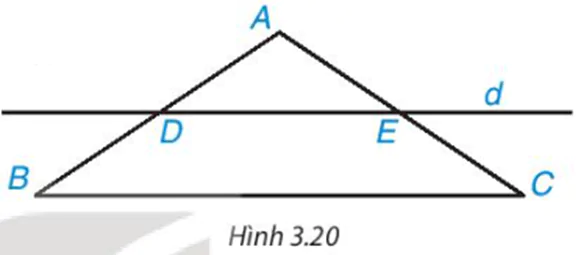
a) Tứ giác DECB là hình gì?
b) Chứng minh BE = CD.
Thực hành trang 55 Toán 8 Tập 1
(H.3.22)

a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:
- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.
- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.
b) Hình thang ABCD có là hình thang cân không? Vì sao?
Vận dụng trang 55 Toán 8 Tập 1
Hãy giải bài toán mở đầu.
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.

Bài 3.4 trang 55 Toán 8 Tập 1
Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?

Bài 3.5 trang 55 Toán 8 Tập 1
Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.
Bài 3.6 trang 55 Toán 8 Tập 1
Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.
Bài 3.7 trang 55 Toán 8 Tập 1
Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.
Bài 3.8 trang 55 Toán 8 Tập 1
Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.