Giải bài tập Bài 6 trang 43 Toán 12 Tập 1 | SGK Toán 12 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 6 trang 43 Toán 12 Tập 1. Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.. SGK Toán 12 - Cánh diều
Đề bài:
Bài 6 trang 43 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) ;
b) ;
c) ;
d) ;
e) ;
f)
Đáp án và cách giải chi tiết:
a)
1) Tập xác định: ℝ\{– 1}.
2) Sự biến thiên
• Các đường tiệm cận:
.
Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.
.
Do đó, đường thẳng là tiệm cận ngang của đồ thị hàm số.
•
• Bảng biến thiên:
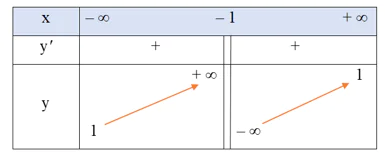
Hàm số đồng biến trên mỗi khoảng (– ∞; – 1) và (– 1; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; – 1).
• Giao điểm của đồ thị với trục hoành: (1; 0).
• Đồ thị hàm số đi qua các điểm (0; – 1), (1; 0), (– 2; 3) và (– 3; 2).
• Đồ thị hàm số nhận giao điểm I(– 1; 1) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
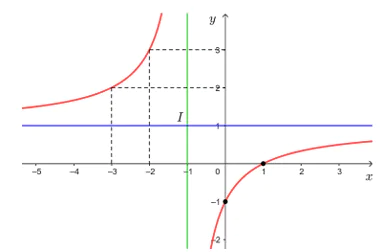
Vậy đồ thị hàm số được cho ở hình trên.
b)
1) Tập xác định: ℝ\{– 1}.
2) Sự biến thiên
• Các đường tiệm cận:
.
Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.
.
Do đó, đường thẳng là tiệm cận ngang của đồ thị hàm số.
• .
• Bảng biến thiên:
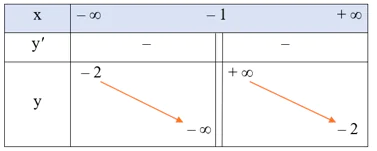
Hàm số nghịch biến trên mỗi khoảng (– ∞; – 1) và (– 1; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Đồ thị hàm số đi qua gốc tọa độ O(0; 0).
• Đồ thị hàm số đi qua các điểm (– 3; – 3), (– 2; – 4), (0; 0) và (1; – 1).
• Đồ thị hàm số nhận giao điểm I(– 1; – 2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
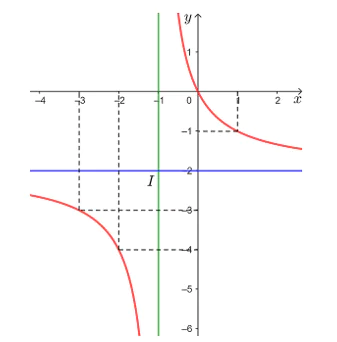
Vậy đồ thị hàm số được cho ở hình trên.
c)
1) Tập xác định: ℝ\{1}.
2) Sự biến thiên
• Các đường tiệm cận:
Ta viết hàm số đã cho dưới dạng: .
Vì nên đồ thị hàm số không có tiệm cận ngang.
.
Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.
; .
Do đó, đường thẳng là tiệm cận xiên của đồ thị hàm số.
• x = – 1 hoặc x = 3.
• Bảng biến thiên:
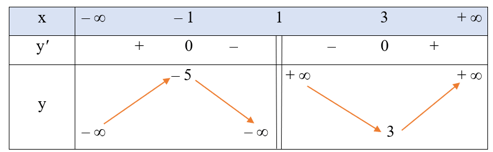
Hàm số đồng biến trên mỗi khoảng (– ∞; – 1) và (3; + ∞); nghịch biến trên mỗi khoảng (– 1; 1) và (1; 3).
Hàm số đạt cực đại tại x = – 1, yCĐ = – 5; đạt cực tiểu tại x = 3, yCT = 3.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; – 6).
• Đồ thị hàm số không cắt trục hoành.
• Đồ thị hàm số đi qua các điểm (– 3; – 6), (– 1; – 5), (0; – 6), (2; 4), (3; 3) và (5; 4).
• Đồ thị hàm số nhận giao điểm I(1; – 1) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
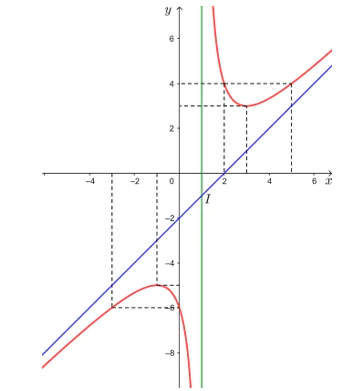
Vậy đồ thị hàm số được cho ở hình trên.
d)
1) Tập xác định: ℝ\{2}.
2) Sự biến thiên
• Các đường tiệm cận:
Ta viết hàm số đã cho dưới dạng: .
Vì nên đồ thị hàm số không có tiệm cận ngang.
. Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.
; . Do đó, đường thẳng là tiệm cận xiên của đồ thị hàm số.
• x = 0 hoặc x = 4.
• Bảng biến thiên:
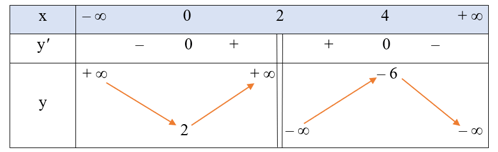
Hàm số đã cho đồng biến trên mỗi khoảng (0; 2) và (2; 4); nghịch biến trên mỗi khoảng (– ∞; 0) và (4; + ∞).
Hàm số đạt cực đại tại x = 4, yCĐ = – 6; đạt cực tiểu tại x = 0, yCT = 2.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; 2).
• Đồ thị hàm số không cắt trục hoành.
• Đồ thị hàm số đi qua các điểm (– 2; 3), (0; 2), (1; 3), (3; – 7), (4; – 6) và (6; – 7).
• Đồ thị hàm số nhận giao điểm I(2; – 2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
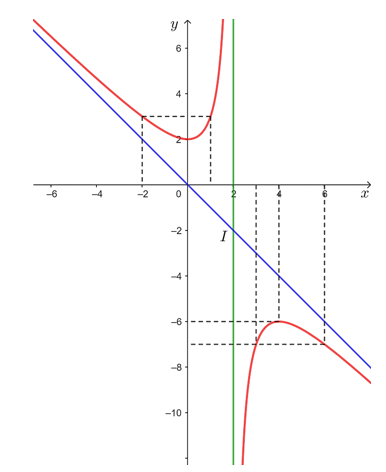
Vậy đồ thị hàm số được cho ở hình trên.
e)
1) Tập xác định: ℝ\{– 2}.
2) Sự biến thiên
• Các đường tiệm cận:
Ta viết hàm số đã cho dưới dạng: .
Vì nên đồ thị hàm số không có tiệm cận ngang.
. Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.
; . Do đó, đường thẳng là tiệm cận xiên của đồ thị hàm số.
• với mọi x ≠ – 2;
• Bảng biến thiên:
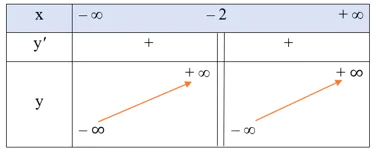
Hàm số đồng biến trên mỗi khoảng (– ∞; – 2) và (– 2; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung:
• Giao điểm của đồ thị với trục hoành: ;
• Đồ thị hàm số đi qua các điểm (– 3; – 4), (– 1; – 6), , ,
• Đồ thị hàm số nhận giao điểm I(– 2; – 5) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
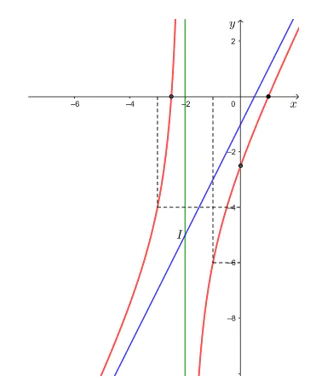
Vậy đồ thị hàm số được cho ở hình trên.
g)
1) Tập xác định: ℝ\{2}.
2) Sự biến thiên
• Các đường tiệm cận:
Ta viết hàm số đã cho dưới dạng: .
Vì nên đồ thị hàm số không có tiệm cận ngang.
. Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.
; . Do đó, đường thẳng là tiệm cận xiên của đồ thị hàm số.
• với mọi x ≠ 2.
• Bảng biến thiên:
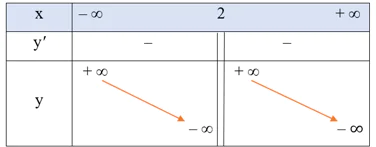
Hàm số đã cho nghịch biến trên mỗi khoảng (– ∞; 2) và (2; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung:
• Giao điểm của đồ thị với trục hoành: (– 1; 0) và (3; 0).
• Đồ thị hàm số đi qua các điểm (– 1; 0), (3; 0), (1; – 4), (5; – 4) và .
• Đồ thị hàm số nhận giao điểm I(2; – 2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
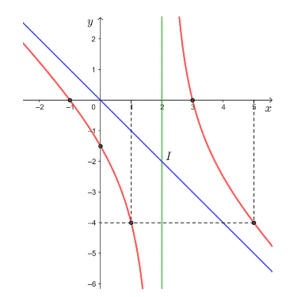
Vậy đồ thị hàm số được cho ở hình trên.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Các công thức liên quan:
Công thức đạo hàm
Bài tập liên quan:
Bài 2 trang 42 Toán 12 Tập 1
Bài 2 trang 42 Toán 12 Tập 1: Đường cong ở Hình 29 là đồ thị của hàm số:
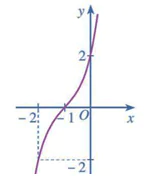
A.
B.
C. .
D. .
Bài 4 trang 43 Toán 12 Tập 1
Bài 4 trang 43 Toán 12 Tập 1: Đường cong ở Hình 30 là đồ thị của hàm số:

Bài 3 trang 43 Toán 12 Tập 1
Bài 3 trang 43 Toán 12 Tập 1: Đường cong nào sau đây là đồ thị của hàm số ?
A.  B.
B.  C.
C. 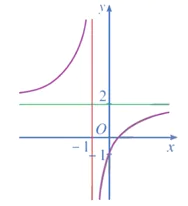 D.
D. 
Bài 7 trang 44 Toán 12 Tập 1
Bài 7 trang 44 Toán 12 Tập 1: Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng.
Trong khoảng 70 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao h của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm
, trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét. (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).
a) Tìm thời điểm t (0 ≤ t ≤ 70) sao cho con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?
b) Vẽ đồ thị của hàm số với 0 ≤ t ≤ 70 (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km).
c) Gọi v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với 0 ≤ t ≤ 70. Xác định hàm số v(t).
d) Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu? Tại thời điểm t = 25 (giây) là bao nhiêu?
e) Tại thời điểm t = 25 (giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
Bài 8 trang 44 Toán 12 Tập 1
Bài 8 trang 44 Toán 12 Tập 1: Xét phản ứng hóa học tạo ra chất C từ hai chất A và B: A + B → C.
Giả sử nồng độ của hai chất A và B bằng nhau [A] = [B] = a (mol/l). Khi đó, nồng độ của chất C theo thời gian t (t > 0) được cho bởi công thức:
(mol/l), trong đó K là hằng số dương (Nguồn: Đỗ Đức Thái (Chủ biên) và các đồng tác giả, Giáo trình Phép tính vi tích phân hàm một biến, NXB Đại học Sư phạm, 2023).
a) Tìm tốc độ phản ứng ở thời điểm t > 0.
b) Chứng minh nếu thì
c) Nêu hiện tượng xảy ra với nồng độ các chất khi t → + ∞.
d) Nêu hiện tượng xảy ra với tốc độ phản ứng khi t → + ∞
Bài 1 trang 42 Toán 12 Tập 1
Bài 1 trang 42 Toán 12 Tập 1: Đồ thị hàm số y = x3 – 3x – 1 là đường cong nào trong các đường cong sau?
A.  B.
B.  C.
C. 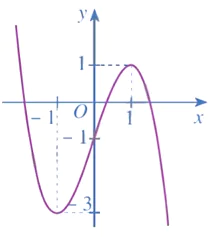 D.
D.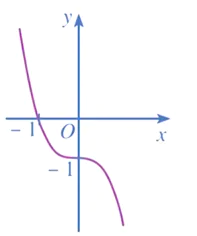
Bài 5 trang 43 Toán 12 Tập 1
Bài 5 trang 43 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) ;
b) ;
c) ;
d) ;
e) ;
g) .
Câu hỏi khởi động trang 28 Toán 12 Tập 1
Câu hỏi khởi động trang 28 Toán 12 Tập 1: Trong 20 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức  , trong đó Q được tính theo m3/phút, t tính theo phút, 0 ≤ t ≤ 20 (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 m3/phút thì cảnh báo lũ được đưa ra.
, trong đó Q được tính theo m3/phút, t tính theo phút, 0 ≤ t ≤ 20 (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 m3/phút thì cảnh báo lũ được đưa ra.
 Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?
Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?
Hoạt động trang 28 Toán 12 Tập 1
Hoạt động trang 28 Toán 12 Tập 1: Lập bảng biến thiên và vẽ đồ thị của hàm số y = x2 – 2x – 3.
Luyện tập 1 trang 29 Toán 12 Tập 1
Luyện tập 1 trang 29 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số 
Luyện tập 3 trang 31 Toán 12 Tập 1
Luyện tập 3 trang 31 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số 
Luyện tập 7 trang 41 Toán 12 Tập 1
Luyện tập 7 trang 41 Toán 12 Tập 1: Trong Ví dụ 9, góc dốc của con đường trên đoạn [– 1 000; 1 000] lớn nhất tại điểm nào?
Luyện tập 2 trang 30 Toán 12 Tập 1
Luyện tập 2 trang 30 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) y = – x3 + 3x – 2;
b) y = x3 + 3x2 + 3x + 1.
Luyện tập 5 trang 34 Toán 12 Tập 1
Luyện tập 5 trang 34 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số  .
.
Luyện tập 4 trang 32 Toán 12 Tập 1
Luyện tập 4 trang 32 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số 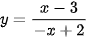
Luyện tập 6 trang 35 Toán 12 Tập 1:
Luyện tập 6 trang 35 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số 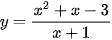 .
.