Giải bài tập Bài 3.42 trang 74 Toán 8 Tập 1 | Toán 8 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 3.42 trang 74 Toán 8 Tập 1. Bài tập cuối chương 3 Tứ giác. Toán 8 - Kết nối tri thức
Đề bài:
Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H.3.59).
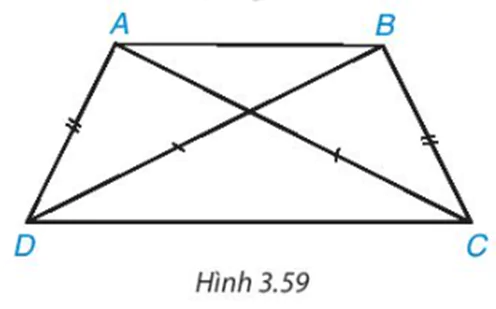
Đáp án và cách giải chi tiết:
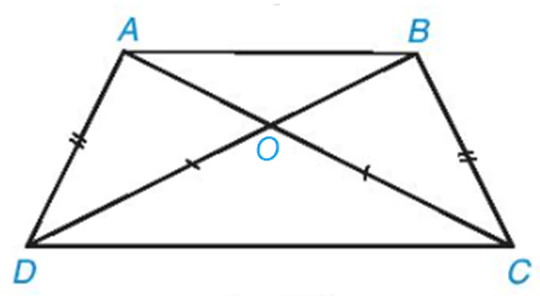
Gọi O là giao điểm của AC và BD.
Xét ∆ABC và ∆BAD có:
BC = AD (giả thiết)
AC = BD (giả thiết)
Cạnh AB chung
Do đó ∆ABC = ∆BAD (c.c.c)
Suy ra (hai góc tương ứng).
Xét ∆ACD và ∆BDC có:
AD = BC (giả thiết)
AC = BD (giả thiết)
Cạnh CD chung
Do đó ∆ADC = ∆BCD (c.c.c)
Suy ra (hai góc tương ứng).
Xét ∆OAD và ∆OBC có:
(chứng minh trên)
AD = BC (giả thiết)
(chứng minh trên)
Do đó ∆OAD = ∆OBC (g.c.g).
Suy ra OA = OB; OC = OD (các cặp cạnh tương ứng).
Khi đó, các tam giác OAB, OCD là tam giác cân tại O.
Suy ra .
Xét ∆OAB và ∆OCD cân tại O có:
• (hai góc đối đỉnh)
•
•
Suy ra mà hai góc này ở vị trí so le trong.
Do đó AB // CD.
Tứ giác ABCD có AB // CD nên ABCD là hình thang.
Hình thang ABCD có hai đường chéo AC = BD.
Do đó tứ giác ABCD là hình thang cân.
Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 3.39 trang 74 Toán 8 Tập 1
Trong các khẳng định sau, khẳng định nào đúng?
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.
C. Nếu tứ giác có hai góc tù thì haigóc còn lại phải nhọn.
D. Không có tứ giác nào có ba góc tù.
Bài 3.40 trang 74 Toán 8 Tập 1
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.
b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.
c) Tứ giác có ba góc vuông là hình chữ nhật.
d) Tứ giác có ba cạnh bằng nhau là hình thoi.
Bài 3.41 trang 74 Toán 8 Tập 1
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.
b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.
d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành.
Bài 3.43 trang 74 Toán 8 Tập 1
Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2AB.
a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?
b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.
Bài 3.44 trang 75 Toán 8 Tập 1
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.60).
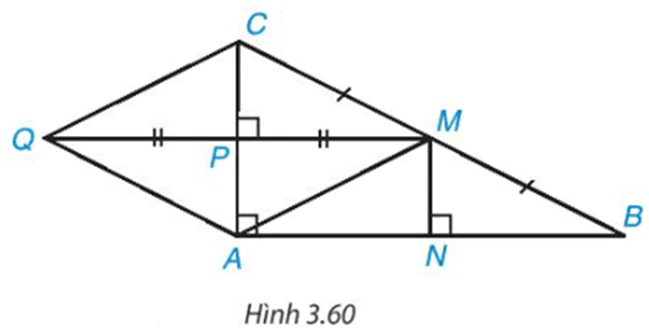
a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau.
b) Chứng minh tứ giác APMN là một hình chữ nhật.
Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC.
c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh tứ giác AMCQ là một hình thoi.
d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?
Bài 3.45 trang 75 Toán 8 Tập 1
Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E, K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N, D lần lượt là chân đường vuông góc hạ từ B xuống ME và từ M xuống AB (H.3.61).
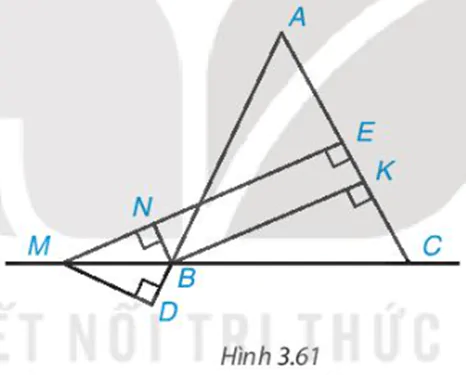
Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật.
b) BK bằng hiệu khoảng cách từ M đến AC và đến AB (dù M thay đổi trên đường thẳng BC miễn là B nằm giữa M và C) tức là BK = ME – MD.