Giải bài tập Bài 3.24 trang 63 Toán 8 Tập 1 | Toán 8 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 3.24 trang 63 Toán 8 Tập 1. Luyện tập chung chương 3 trang 63. Toán 8 - Kết nối tri thức
Đề bài:
Cho ba điểm không thẳng hàng.
a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành. Hãy vẽ hình và mô tả cách tìm.
b) Hỏi tìm được bao nhiêu điểm như vậy?
Đáp án và cách giải chi tiết:
a) Gọi ba điểm không thẳng hàng đó là A, B, C. Khi đó ta cần tìm điểm D để bốn điểm A, B, C, D là bốn đỉnh của một hình bình hành (H).
• Nếu đỉnh đối của D trong hình bình hành (H) là B thì trung điểm của BD trùng với trung điểm của AC;
• Ngược lại, lấy điểm D sao cho trung điểm của BD trùng với trung điểm của AC thì (H) là hình bình hành ABCD cần tìm.
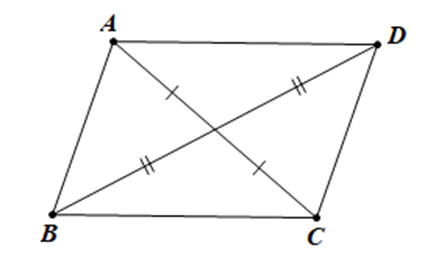
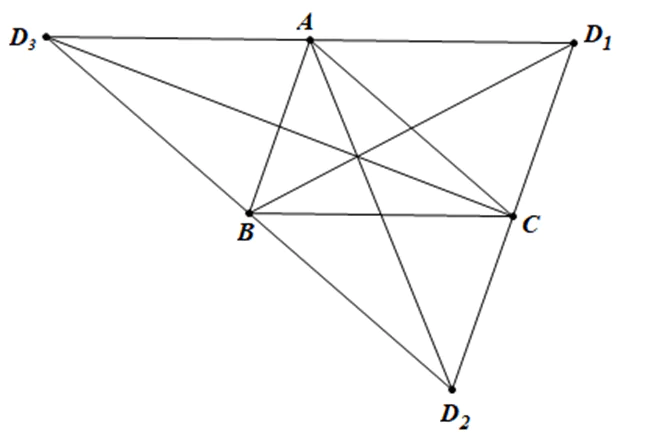
b) Từ câu a, suy ra có ba điểm D như vậy là D1, D2 và D3.
• Khi D là đỉnh đối của B thì theo câu a, (H) là hình bình hành ABCD1;
• Khi D là đỉnh đối của A thì (H) là hình bình hành ABD2C;
• Khi D là đỉnh đối của C thì (H) là hình bình hành ACBD3.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 3.19 trang 63 Toán 8 Tập 1
Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?

Bài 3.20 trang 63 Toán 8 Tập 1
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
a) AN = CM;
b) .
Bài 3.21 trang 63 Toán 8 Tập 1
Vẽ tứ giác ABCD theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB.
Bước 2. Lấy điểm C ∈ a.
Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.
Hãy giải thích tại sao tứ giác ABCD là hình bình hành.
Bài 3.22 trang 63 Toán 8 Tập 1
Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.
a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
b) Tính khoảng cách từ giao điểm đó đến điểm C.
Bài 3.23 trang 63 Toán 8 Tập 1
Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành;
b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.