Giải bài tập Bài 3 trang 88 Toán 8 Tập 1 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 88 Toán 8 Tập 1. Bài tập cuối chương 3 Định lý Pythagore. Các loại tứ giác thường gặp. Toán 8 - Chân trời sáng tạo
Đề bài:
Bài 3 trang 88 Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào sai?
A. Tứ giác có ba góc vuông là hình chữ nhật.
B. Hình bình hành có một góc vuông là hình chữ nhật.
C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
D. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Đáp án và cách giải chi tiết:
Đáp án đúng là: C
Theo tính chất hình bình hành: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Do đó đây là tính chất đã có sẵn của hình bình hành, nên khẳng định C là sai.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 88 Toán 8 Tập 1
Bài 1 trang 88 Toán 8 Tập 1: Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó có 2 đoạn tre dài 60 cm và 80 cm để làm hai đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều. Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là
A. 5 m.
B. 1 m.
C. 1,5 m.
D. 2 m.
Bài 2 trang 88 Toán 8 Tập 1
Bài 2 trang 88 Toán 8 Tập 1: Cho hình thang cân ABCD (AB // CD) có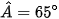 
. Số đo góc C là
A. 115°.
B. 95°.
C. 65°.
D. 125°.
Bài 4 trang 88 Toán 8 Tập 1
Bài 4 trang 88 Toán 8 Tập 1: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Biết AB = 8 cm; AC = 15 cm. Độ dài đoạn AM là
A. 8,5 cm.
B. 8 cm.
C. 7 cm.
D. 7,5 cm.
Bài 5 trang 88 Toán 8 Tập 1
Bài 5 trang 88 Toán 8 Tập 1: Cho hình thoi ABCD có cạnh bằng 13 cm, độ dài đường chéo AC là 10 cm. Độ dài đường chéo BD là
A. 24 cm.
B. 12 cm.
C. 16 cm.
D. 20 cm.
Bài 6 trang 88 Toán 8 Tập 1
Bài 6 trang 88 Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào đúng?
A. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.
B. Hình thoi có hai đường chéo vuông góc là hình vuông.
C. Hình thoi có một góc vuông là hình vuông.
D. Hình chữ nhật có một góc vuông là hình vuông.
Bài 7 trang 88 Toán 8 Tập 1
Bài 7 trang 88 Toán 8 Tập 1: Cho tứ giác ABCD, biết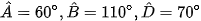 
. Khi đó số đo góc C là
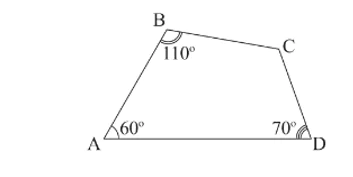
A. 120°.
B. 110°.
C. 130°.
D. 80°.
Bài 8 trang 89 Toán 8 Tập 1
Bài 8 trang 89 Toán 8 Tập 1: Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD, N là giao điểm của DE và AB. Chứng minh rằng:
a) M, N theo thứ tự là trung điểm của CD, AB;
b) EMFN là hình bình hành.
Bài 9 trang 89 Toán 8 Tập 1
Bài 9 trang 89 Toán 8 Tập 1: Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.
a) Chứng minh rằng tứ giác ADHC là hình thang.
b) Gọi E là điểm đối xứng với H qua D. Chứng minh rằng tứ giác AHBE là hình chữ nhật.
c) Tia CD cắt AH tại M và cắt BE tại N. Chứng minh rằng tứ giác AMBN là hình bình hành.
Bài 10 trang 89 Toán 8 Tập 1
Bài 10 trang 89 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh rằng tứ giác ANEB là hình thang vuông.
b) Chứng minh rằng tứ giác ANEM là hình chữ nhật.
c) Qua M kẻ đường thẳng song song với BN cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.
d) Gọi D là điểm đối xứng của E qua M. Chứng minh rằng A là trung điểm của DF.
Bài 11 trang 89 Toán 8 Tập 1
Bài 11 trang 89 Toán 8 Tập 1: Cho hình bình hành ABCD có AB = 2AD. Gọi E và F lần lượt là trung điểm của AB và CD, I là giao điểm của AF và DE, K là giao điểm của BF và CE.
a) Chứng minh rằng tứ giác AECF là hình bình hành.
b) Tứ giác AEFD là hình gì? Vì sao?
c) Chứng minh rằng tứ giác EIFK là hình chữ nhật.
d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông.
Bài 12 trang 89 Toán 8 Tập 1
Bài 12 trang 89 Toán 8 Tập 1: Cho hình bình hành ABCD có AD = 2AB. Từ C vẽ CE vuông góc với AB tại E. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE tại F, MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
b) Chứng minh tam giác EMC cân tại M.
c) Chứng minh rằng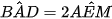 
Hướng dẫn:
b) Chứng minh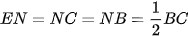 
c) Chứng minh 