Giải bài tập Khởi động trang 52 Toán 8 Tập 2 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Khởi động trang 52 Toán 8 Tập 2. Bài 2. Đường trung bình của tam giác.. Toán 8 - Chân trời sáng tạo
Đề bài:
Giữa hai điểm B và C có một hồ nước (xem hình bên). Biết DE = 45 m. Làm thế nào để tính được khoảng cách giữa hai điểm B và C?
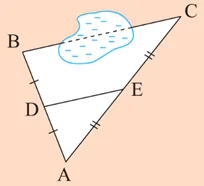
Đáp án và cách giải chi tiết:
Xét tam giác ABC, ta có:
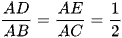
Theo định lí Thalès đảo, ta có DE // BC.
Suy ra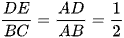 
, vậy BC = 2DE = 90 m.
Sau khi học xong bài này:
Ta có: D, E là trung điểm của AB và AC nên DE là đường trung bình của tam giác ABC
Suy ra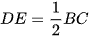 
, vậy BC = 2DE = 90 m.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khám phá 1 trang 52 Toán 8 Tập 2
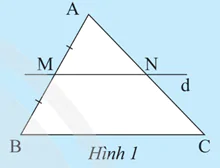
Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của AC.
Vận dụng 1 trang 53 Toán 8 Tập 2
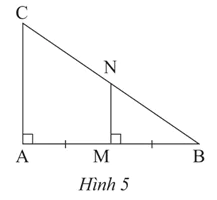
Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC.
Khám phá 2 trang 53 Toán 8 Tập 2
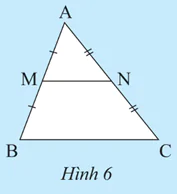
Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC.
a) Tính các tỉ số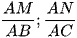 
;
b) Chứng minh MN // BC;
c) Chứng minh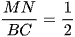 
.
Thực hành 2 trang 53 Toán 8 Tập 2
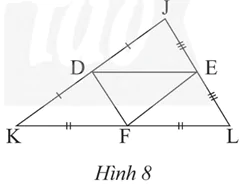
Trong Hình 8, cho biết JK = 10 cm, DE = 6,5 cm, EL = 3,7 cm. Tính DJ, EF, DF, KL.
Vận dụng 2 trang 53 Toán 8 Tập 2
Hãy tính khoảng cách BC trong phần Hoạt động khởi động (trang 52).
Bài 1 trang 53 Toán 8 Tập 2
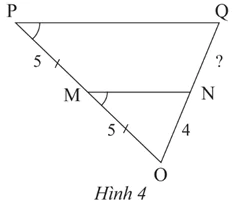
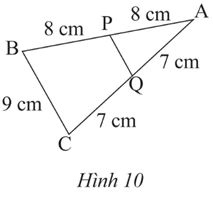
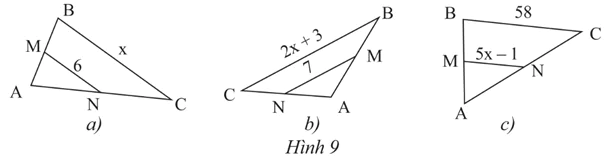
Cho MN là đường trung bình của mỗi tam giác ABC trong Hình 9. Hãy tìm giá trị x trong mỗi hình.
Bài 3 trang 54 Toán 8 Tập 2
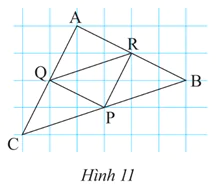
Cho biết cạnh mỗi ô vuông bằng 1 cm. Tính độ dài các đoạn PQ, PR, RQ, AB, BC, CA trong Hình 11.
Bài 4 trang 54 Toán 8 Tập 2
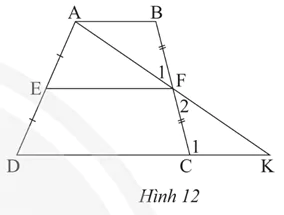
Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC (Hình 12).
a) Tam giác FBA và tam giác FCK có bằng nhau không? Vì sao?
b) Chứng minh EF // CD // AB.
c) Chứng minh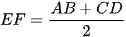 
.
Bài 5 trang 54 Toán 8 Tập 2
Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Bài 6 trang 54 Toán 8 Tập 2
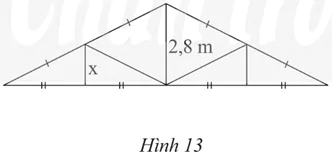
Một mái nhà được vẽ lại như Hình 13. Tính độ dài x trong hình mái nhà.
Bài 7 trang 54 Toán 8 Tập 2
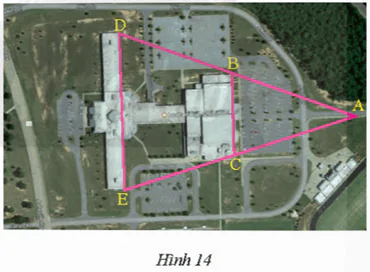
Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh DE, cho biết BC = 232 m và B, C lần lượt là trung điểm AD và AE.
