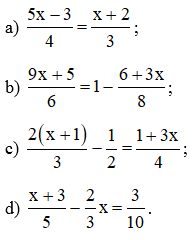Giải bài tập Khám phá 1 trang 31 Toán 8 Tập 2 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Khám phá 1 trang 31 Toán 8 Tập 2. Bài 1. Phương trình bậc nhất một ẩn.. Toán 8 - Chân trời sáng tạo
Đề bài:
a) Ở Hoạt động khởi động trên, viết các biểu thức biểu thị tổng khối lượng của các vật trên mỗi đĩa cân. Từ điều kiện cân thăng bằng, hai biểu thức có mối quan hệ như thế nào?
b) Nếu x = 200 thì cân có thăng bằng không? Tại sao?
Nếu x = 100 thì cân có thăng bằng không? Tại sao?
Đáp án và cách giải chi tiết:
a) Tổng khối lượng của các vật trên đĩa cân bên trái: 4x (g)
Tổng khối lượng của các vật trên đĩa cân bên phải: 600 + x (g)
Với điều kiện cân thăng bằng thì mối quan hệ của hai biểu thức là 4x = 600 + x
b) • Nếu x = 200:
Tổng khối lượng của các vật trên đĩa cân bên trái: 4 . 200 = 800 (g)
Tổng khối lượng của các vật trên đĩa cân bên phải: 600 + 200 = 800 (g)
Tổng khối lượng của các vật trên hai đĩa cân bằng nhau nên cân thăng bằng.
• Nếu x = 100:
Tổng khối lượng của các vật trên đĩa cân bên trái: 4 . 100 = 400 (g)
Tổng khối lượng của các vật trên đĩa cân bên phải: 600 + 100 = 700 (g)
Vì 700 > 400 nên tổng khối lượng của các vật trên hai đĩa cân không bằng nhau. Do đó cân không thăng bằng.
Vậy nếu x = 200 thì cân thăng bằng, nếu x = 100 thì cân không thăng bằng.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 31 Toán 8 Tập 2
Quan sát hình bên. Biết rằng cân thăng bằng, có thể tìm được khối lượng quả cân 
không? Tìm bằng cách nào?
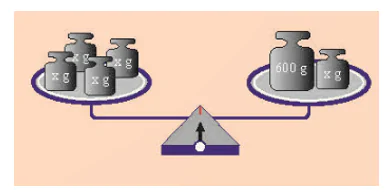
Thực hành 1 trang 32 Toán 8 Tập 2
Cho phương trình 4t – 3 = 12 – t. Trong hai số 3 và 5, có số nào là nghiệm của phương trình đã cho không?
Vận dụng 1 trang 32 Toán 8 Tập 2
Đặt lên hai đĩa những quả cân như Hình 1.
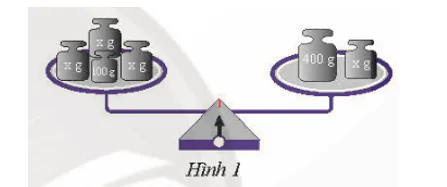
a) Biết rằng cân thăng bằng, hãy viết phương trình biểu thị sự thăng bằng này.
b) Nếu x = 100 thì cân có thăng bằng không? Vì sao?
Nếu x = 150 thì cân có thăng bằng không? Vì sao?
Từ đó, chỉ ra một nghiệm của phương trình ở câu a.
Khám phá 2 trang 32 Toán 8 Tập 2
Xét cân thăng bằng ở Hoạt động khởi động.
a) Giải thích tại sao nếu ra khỏi đĩa cân một quả cân 
thì cân vẫn thăng bằng.
b) Nếu thay quả cân 
bằng ba quả cân 
(Hình 2) thì cân còn cân bằng không? Tại sao?
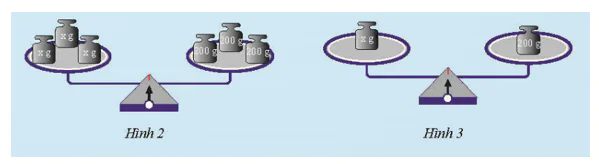
c) Tiếp theo, chia các quả cân trên mỗi đĩa cân thành ba phần bằng nhau, rồi bỏ đi hai phần (Hình 3). Khi đó, cân còn cân bằng không? Tại sao?
;
.Thực hành 3 trang 34 Toán 8 Tập 2
Giải các phương trình sau:
a) 15 – 4x = x – 5;
b)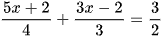 
.
Vận dụng 2 trang 35 Toán 8 Tập 2
Hai bạn An và Mai giải phương trình x = 2x như sau:
An: x = 2x
1 = 2 (chia hai vế cho x)
Vậy phương trình vô nghiệm.
Mai: x = 2x
x – 2x = 0 (chuyển 2x sang vế trái)
−x = 0 (rút gọn)
x = 0 (nhân hai vế với −1)
Vậy phương trình có nghiệm x = 0.
Em hãy cho biết bạn nào giải đúng.
Bài 1 trang 35 Toán 8 Tập 2
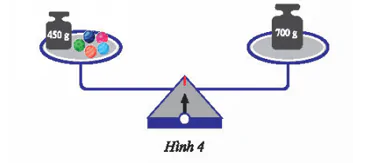
Trong Hình 4, cho biết các viên bi có cùng khối lượng là x (g) và cân thăng bằng.
Viết phương trình biểu diễn liên hệ giữa khối lượng các vật ở trên hai đĩa cân.
Bài 2 trang 36 Toán 8 Tập 2
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? Xác định các hệ số a, b của phương trình bậc nhất một ẩn đó:
a)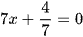 
;
b)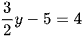 
;
c) 0t + 6 = 0;
d) x2 + 3 = 0.
Bài 3 trang 36 Toán 8 Tập 2
Giải các phương trình sau:
a) 5x – 30 = 0;
b) 4 – 3x = 11;
c) 3x + x + 20 = 0;
d)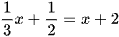 
.
Bài 4 trang 36 Toán 8 Tập 2
Giải các phương trình sau:
a) 8 – (x – 15) = 2(3 – 2x);
b) –6(1,5 – 2u) = 3(–15 + 2u);
c) (x + 3)2 − x(x + 4) = 13;
d) (y + 5)(y − 5) − (y − 2)2 = −5.
Bài 6 trang 36 Toán 8 Tập 2
Tìm x, biết rằng nếu lấy x trừ đi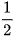 
, rồi nhân kết quả với 
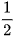thì được 
.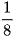
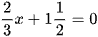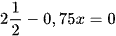