Giải bài tập Bài 9.13 trang 92 Toán 8 Tập 2 | Toán 8 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 9.13 trang 92 Toán 8 Tập 2. Luyện tập chung chương 9 trang 91.. Toán 8 - Kết nối tri thức
Đề bài:
Cho hình thang ABCD (AB // CD) có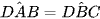 
.
a) Chứng minh rằng ΔABD ∽ ΔBDC.
b) Giả sử AB = 2 cm, AD = 3 cm, BD = 4 cm. Tính độ dài các cạnh BC và DC.
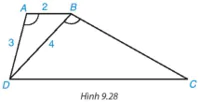
Đáp án và cách giải chi tiết:
a) Vì AB // CD (giả thiết) nên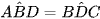 
(2 góc ở vị trí so le trong).
+ Xét ΔABD và ΔBDC có: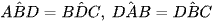 
.
Suy ra ΔABD ∽ ΔBDC (g.g).
b) Ta có: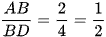 
.
Vậy ΔABD ∽ ΔBDC với tỉ số đồng dạng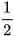 
.
Suy ra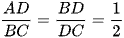 
hay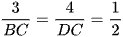 
.
Suy ra BC = 2.3 = 6 cm; DC = 4.2 = 8 cm.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 9.11 trang 92 Toán 8 Tập 2
Cho ΔABC ∽ ΔDEF. Biết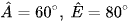 
, hãy tính số đo các góc 
.
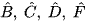Bài 9.12 trang 92 Toán 8 Tập 2
Cho ΔABC ∽ ΔA'B'C'. Biết AB = 3 cm, A′B′ = 6 cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'.
Bài 9.14 trang 92 Toán 8 Tập 2
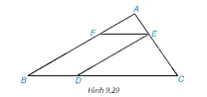
Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, DE = 4 cm, AB = 6 cm. Chứng minh rằng ΔAEF ∽ ΔECD và tính tỉ số đồng dạng.
Bài 9.15 trang 92 Toán 8 Tập 2
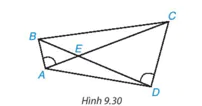
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng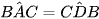 
. Chứng minh rằng ΔAED ∽ ΔBEC.
Bài 9.16 trang 92 Toán 8 Tập 2
Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM = MD, 2BN = NC. Biết AB = 5 cm, CD = 6 cm, hãy tính độ dài đoạn thẳng MN.