Giải bài tập Bài 8 trang 41 Toán 8 Tập 2 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 8 trang 41 Toán 8 Tập 2. Bài tập cuối chương 6.. Toán 8 - Chân trời sáng tạo
Đề bài:
Giải các phương trình sau:
a) 10 − (x − 5) = 20;
b) −12 + 3(1,5 − 3u) = 15;
c) (x + 2)2 − x(x − 3) = −12;
d) (x + 5)(x − 5) − (x − 3)2 = 6.
Đáp án và cách giải chi tiết:
a) 10 − (x − 5) = 20
10 − x + 5 = 20
x = 10 + 5 − 20
x = −5
Vậy phương trình đã cho có nghiệm là x = −5.
b) −12 + 3(1,5 − 3u) = 15
−12 + 4,5 − 9u = 15
9u = −12 + 4,5 − 15
9u = −22,5
u = −2,5
Vậy phương trình đã cho có nghiệm là u = −2,5.
c) (x + 2)2 − x(x − 3) = −12
x2 + 4x + 4 − x2 + 3x = −12
7x = −16
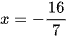
Vậy phương trình đã cho có nghiệm là 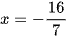 .
.
d) (x + 5)(x − 5) − (x − 3)2 = 6
x2 – 25 − x2 + 6x – 9 = 6
6x = 40
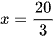
Vậy phương trình đã cho có nghiệm là 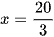 .
.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 41 Toán 8 Tập 2
Phương trình ax + b = 0 là phương trình bậc nhất một ẩn nếu
A. a = 0;
B. b ≠ 0;
C. b = 0;
D. a ≠ 0.
Bài 2 trang 41 Toán 8 Tập 2
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
A. 3x + 2y − 6 = 0;
B. 3x + 6 = 0;
C. x2 = 4;
D. y2 – x + 1 = 0.
Bài 3 trang 41 Toán 8 Tập 2
Phương trình nào sau đây nhận x = 2 là nghiệm?
A. 3x + 6 = 0;
B. 2x − 4 = 0;
C. 2x + 3 = 1 + x;
D. x + 2 = 4 + x.
Bài 4 trang 41 Toán 8 Tập 2
Nghiệm của phương trình 5x + 3 = 18 là:
A. x = −3;
B. x = 5;
C. x = 3;
D. x = −5.
Bài 5 trang 41 Toán 8 Tập 2
Phương trình x − 4 = 10 − x có nghiệm là:
A. 3;
B. 14;
C. 7;
D. −7.
Bài 6 trang 41 Toán 8 Tập 2
Cho biết 3x – 9 = 0. Khi đó giá trị của biểu thức x2 − 2x − 3 là:
A. –3;
B. 1;
C. 0;
D. 6.
Bài 7 trang 41 Toán 8 Tập 2
Giải các phương trình sau:
a) 5x – 12 = 3;
b) 2,5y + 6 = –6,5;
c) 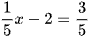 ;
;
d) 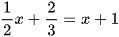 .
.
Bài 10 trang 42 Toán 8 Tập 2
Một tổ may có kế hoạch mỗi ngày phải may 30 chiếc áo. Trong thực tế mỗi ngày tổ đã may được 40 chiếc áo. Do đó xưởng đã hoàn thành kế hoạch sớm hơn 3 ngày và may thêm được 20 chiếc áo nữa. Tính số áo mà tổ phải may theo kế hoạch.
Bài 11 trang 42 Toán 8 Tập 2
Trong một cuộc thi, học sinh cần trả lời 50 câu hỏi trắc nghiệm, mỗi câu trả lời đúng được 5 điểm, mỗi câu trả lời sai (hoặc không trả lời) bị trừ 2 điểm. An đã tham gia cuộc thi trên và đã thi được tổng cộng 194 điểm. Hỏi An trả lời đúng mấy câu?
Bài 12 trang 42 Toán 8 Tập 2
Biết rằng trong 500 g dung dịch nước muối chứa 150 g muối nguyên chất. Hỏi cần phải thêm vào dung dịch đó bao nhiêu gam nước để dung dịch có nồng độ là 20%?
Bài 13 trang 42 Toán 8 Tập 2
Một ô tô dự định đi từ A đến B với tốc độ 50 km/h. Sau khi đi được 23 quãng đường với tốc độ đó, vì đường xấu nên người lái xe đã giảm tốc độ còn 40 km/h trên quãng đường còn lại. Vì thế ô tô đã đến B chậm hơn dự định 30 phút. Tính chiều dài quãng đường AB.
Bài 14 trang 42 Toán 8 Tập 2
Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu tăng chiều dài thêm 3 m và giảm chiều rộng 2 m thì diện tích giảm 90 m2. Tính chiều dài và chiều rộng của hình chữ nhật.
Bài 15 trang 42 Toán 8 Tập 2
Trong tháng 4, một công nhân nhận được tiền lương là 7 800 000 đồng gồm tiền lương của 24 ngày làm việc bình thường và 4 ngày làm tăng ca (ngày chủ nhật và ngày lễ). Biết tiền lương của một ngày tăng ca nhiều hơn tiền lương của một ngày làm việc bình thường là 200 000 đồng. Tính tiền lương của một ngày làm việc bình thường.
Bài 16 trang 42 Toán 8 Tập 2
Một siêu thị điện máy có chương trình khuyến mãi giảm giá tủ lạnh, sau hai lần giảm giá, mỗi lần giảm 20% so với giá tại thời điểm đó thì giá bán của một chiếc tủ lạnh là 12 800 000 đồng. Tính giá tiền tủ lạnh đó lúc chưa giảm giá lần nào.
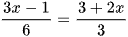 ;
;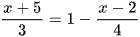 ;
;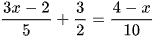 ;
;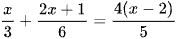 .
.