Giải bài tập Bài 8 trang 40 Toán 8 Tập 2 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 8 trang 40 Toán 8 Tập 2. Bài 2. Giải bài toán bằng cách lập phương trình bậc nhất.. Toán 8 - Chân trời sáng tạo
Đề bài:
Để khuyến khích tiết kiệm điện, giá bán lẻ điện sinh hoạt năm 2022 được tính lũy tiến, nghĩa là sử dụng càng nhiều điện thì giá mỗi kWh càng tăng theo các mức như sau:
Mức 1: Tính cho 50 kWh đầu tiên.
Mức 2: Tính cho số kWh từ 51 đến 100 kWh, mỗi kWh ở mức 2 cao hơn 56 đồng so với mức 1.
Mức 3: Tính cho số kWh từ 101 đến 200 kWh, mỗi kWh ở mức 3 cao hơn 280 đồng so với mức 2.
Mức 4: Tính cho số kWh từ 201 đến 300 kWh, mỗi kWh ở mức 4 cao hơn 522 đồng so với ở mức 3.
...
Ngoài ra, người sử dụng điện còn phải trả thêm 10% thuế giá trị gia tăng.
Tháng vừa rồi nhà bạn Minh đã sử dụng hết 185 kWh và phải trả 375 969 đồng. Hỏi mỗi kWh ở mức 3 giá bao nhiêu?
Đáp án và cách giải chi tiết:
Gọi x (đồng) là giá mỗi số điện ở mức thứ nhất (x > 0).
Khi đó, ta có:
Giá mỗi số điện ở mức 2 là: x + 56 (đồng)
Giá mỗi số điện ở mức 3 là: x + 56 + 280 = x + 336 (đồng)
Giá mỗi số điện ở mức 4 là : x + 336 + 522 = x + 858 (đồng)
Nhà Minh dùng hết 185 số điện = 50 + 50 + 85.
Như vậy nhà Minh phải đóng cho 50 số điện ở mức 1, 50 số điện ở mức 2 và 85 số điện ở mức 3.
Giá tiền 50 số điện mức đầu tiên là: 50x (đồng)
Giá tiền 50 số điện mức thứ hai là: 50(x + 56) (đồng)
Giá tiền 85 số điện còn lại mức thứ ba là: 85(x + 336) (đồng).
Khi đó, số tiền điện (chưa tính VAT) của nhà Cường bằng:
50x + 50(x + 56) + 85(x + 336)
= 50x + 50x + 2800 + 85x + 28 560
= 185x + 31 360
Thuế VAT nhà Cường phải trả là: 0,1(185x + 31 360)
Tổng số tiền điện nhà Cường phải đóng (tiền gốc + thuế) bằng:
1,1(185x + 31 360)
Thực tế nhà Cường hết 95 700 đồng nên ta có phương trình:
1,1(185x + 31 360) = 375 969
⇔ 203,5x + 34 496 = 375 969
⇔ 203,5x = 341 473
⇔ x = 1678 (đồng) (thỏa mãn điều kiện).
Vậy mỗi số điện ở mức giá thứ 3 là 1678 + 336 = 2014 (đồng).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 37 Toán 8 Tập 2
Sau khi giảm giá 15% thì đôi giày thể thao có giá là 1 275 000 đồng. Hỏi lúc chưa giảm giá thì đôi giày có giá là bao nhiêu?
Khám phá 1 trang 37 Toán 8 Tập 2
Một mảnh vườn hình chữ nhật có chiều rộng là x (m), chiều dài hơn chiều rộng 20 m.
Hãy viết biểu thức với biến x biểu thị:
a) Chiều dài của hình chữ nhật;
b) Chu vi của hình chữ nhật;
c) Diện tích của hình chữ nhật.
Thực hành 1 trang 37 Toán 8 Tập 2
Tiền lương cơ bản của anh Minh mỗi tháng là x (triệu đồng). Tiền phụ cấp mỗi tháng là 3 500 000 đồng.
a) Viết biểu thức biểu thị tiền lương mỗi tháng của anh Minh. Biết tiền lương mỗi tháng bằng tổng tiền lương cơ bản và tiền phụ cấp.
b) Tháng Tết, anh Minh được thưởng 1 tháng lương cùng với 60% tiền phụ cấp. Viết biểu thức chỉ số tiền anh Minh được nhận ở tháng Tết.
Khám phá 2 trang 38 Toán 8 Tập 2
Thay dấu 
bằng các dữ liệu thích hợp để hoàn thành lời giải bài toán.
Một người đi xe gắn máy từ A đến B với tốc độ 40 km/h. Lúc về người đó đi với tốc độ 50 km/h nên thời gian về ít hơn thời gian đi là 30 phút. Tìm chiều dài quãng đường AB.
Gọi chiều dài quãng đường AB là x (km). Điều kiện x > .
Thời gian đi là: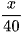 
giờ.
Thời gian về là: .
Ta có: 30 phút =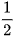 
giờ.
Vì thời gian về ít hơn thời gian đi là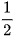 
giờ nên ta có phương trình:
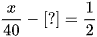
Giải phương trình, ta được x = thỏa mãn điều kiện x > .
Vậy chiều dài của quãng đường AB là .
Thực hành 2 trang 39 Toán 8 Tập 2
Một người mua 36 bông hoa hồng và hoa cẩm chướng hết tất cả 136 800 đồng. Giá mỗi bông hoa hồng là 3000 đồng, giá mỗi bông hoa cẩm chướng là 4800 đồng. Tính số bông hoa mỗi loại.
Vận dụng trang 39 Toán 8 Tập 2
Giải bài toán đã cho trong Hoạt động khởi động (trang 37).
Bài 1 trang 39 Toán 8 Tập 2
Một nhân viên giao hàng trong hai ngày đã giao được 95 đơn hàng. Biết số đơn hàng ngày thứ hai giao được nhiều hơn ngày thứ nhất là 15 đơn. Tính số đơn hàng nhân viên đó giao được trong ngày thứ nhất.
Bài 2 trang 39 Toán 8 Tập 2
Anh Bình tiêu hao 14 calo cho mỗi phút bơi và 10 calo cho mỗi phút chạy bộ. Trong 40 phút với hai hoạt động trên, anh Bình đã tiêu hao 500 calo. Tính thời gian chạy bộ của anh Bình.
Bài 3 trang 40 Toán 8 Tập 2
Một cửa hàng ngày thứ nhất bán được nhiều hơn ngày thứ hai 560 kg gạo. Tính số gạo cửa hàng bán được trong ngày thứ nhất, biết rằng nếu ngày thứ nhất bán được thêm 60 kg gạo thì sẽ gấp 1,5 lần ngày thứ hai.
Bài 4 trang 40 Toán 8 Tập 2
Một xe tải đi từ A đến B với tốc độ 50 km/h. Khi từ B quay về A xe chạy với tốc độ 40 km/h. Thời gian cả đi lẫn về mất 5 giờ 24 phút không kể thời gian nghỉ. Tính chiều dài quãng đường AB.
Bài 5 trang 40 Toán 8 Tập 2
Bác Năm gửi tiết kiệm một số tiền tại một ngân hàng theo thể thức kì hạn một năm với lãi suất 6,2%/năm, tiền lãi sau mỗi năm gửi tiết kiệm sẽ được nhập vào tiền vốn để tính lãi cho năm tiếp theo. Sau hai năm gửi bác Năm rút hết tiền về và nhận được cả vốn lẫn lãi là 225 568 800 đồng. Hỏi số tiền ban đầu bác Năm gửi tiết kiệm là bao nhiêu?
Bài 6 trang 40 Toán 8 Tập 2
Tổng số học sinh khối 8 và khối 9 của một trường là 580 em, trong đó có 256 em là học sinh giỏi. Tính số học sinh mỗi khối, biết rằng số học sinh giỏi khối 8 chiếm tỉ lệ 40% số học sinh khối 8, số học sinh giỏi khối 9 chiếm tỉ lệ 48% số học sinh khối 9.
Bài 7 trang 40 Toán 8 Tập 2
Một lọ dung dịch chứa 12% muối. Nếu pha thêm 350g nước vào lọ thì được một dung dịch 5% muối. Tính khối lượng dung dịch trong lọ lúc đầu.