Giải bài tập Bài 6 trang 95 Toán 8 Tập 2 | Toán 8 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 6 trang 95 Toán 8 Tập 2. Bài tập cuối chương 9.. Toán 8 - Chân trời sáng tạo
Đề bài:
Một hộp chứa 6 tấm thể cùng loại được đánh số lần lượt là 2; 3; 5; 8; 13; 21. Lấy ngẫu nhiên 1 thẻ từ hộp. Tính xác suất của các biến cố:
A: "Số ghi trên thẻ là số chẵn";
B: "Số ghi trên thẻ là số nguyên tố";
C: "Số ghi trên thẻ là số chính phương".
Đáp án và cách giải chi tiết:
Có 2 kết quả thuận lợi cho biến cố A là: 2; 8.
Xác suất của biến cố A là: 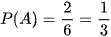 .
.
Có 4 kết quả thuận lợi cho biến cố B là: 2; 3; 5; 13.
Xác suất của biến cố B là: 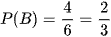 .
.
Có 0 kết quả thuận lợi cho biến cố C
Xác suất của biến cố C là: P(C) = 0.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 95 Toán 8 Tập 2
Một hộp chứa 10 tấm thẻ cùng loại được đánh số từ 4 đến 13. Hà lấy ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số nguyên tố là
A. 0,2;
B. 0,3;
C. 0,4;
D. 0,5.
Bài 2 trang 95 Toán 8 Tập 2
Một hộp chứa các thẻ màu xanh và thẻ màu đỏ có kích thước và khối lượng như nhau. Thọ lấy ra ngẫu nhiên 1 thẻ từ hộp, xem màu rồi trả lại hộp. Lặp lại thử nghiệm đó 50 lần, Thọ thấy có 14 lần lấy được thẻ màu xanh. Xác suất thực nghiệm của biến cố "Lấy được thẻ màu đỏ" là
A. 0,14;
B. 0,28;
C. 0,72;
D. 0,86.
Bài 3 trang 95 Toán 8 Tập 2
Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là 16%. Gặp ngẫu nhiên một học sinh, xác suất học sinh đó không bị cận thị là
A. 0,16;
B. 0,94;
C. 0,84;
D. 0,5.
Bài 4 trang 95 Toán 8 Tập 2
Vĩnh gieo 3 con xúc xắc cân đối và đồng chất. Xác suất của biến cố "Tích số chấm xuất hiện trên ba con xúc xắc bằng 28" là
A. 0;
B. 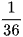 ;
;
C. 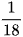 ;
;
D. 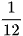 .
.
Bài 5 trang 95 Toán 8 Tập 2
Thúy gieo một con xúc xắc cân đối 1000 lần. Số lần xuất hiện mặt 6 chấm trong 1000 lần gieo đó có khả năng lớn nhất thuộc vào tập hợp nào dưới đây?
A. {0; 1;...; 100};
B. {101; 102; ...; 200};
C. {201; 202; ...; 300};
D. {301; 302; ..; 400}.
Bài 7 trang 95 Toán 8 Tập 2
Một túi đựng 1 viên bi xanh, 1 viên bi đỏ, 1 viên bi trắng và 1 viên bi vàng có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 2 viên bi từ túi. Tính xác suất của các biến cố:
A: "Trong hai viên bi lấy ra có 1 viên màu đỏ";
B. "Hai viên bi lấy ra đều không có màu trắng".
Bài 8 trang 95 Toán 8 Tập 2
Tỉ lệ vận động viên đạt huy chương trong một đại hội thể thao là 21%. Gặp ngẫu nhiên một vận động viên dự đại hội. Tính xác suất của biến cố vận động viên ấy đạt huy chương.
Bài 9 trang 96 Toán 8 Tập 2
Thảo tung hai đồng xu giống nhau 100 lần và ghi lại kết quả ở bảng sau:

Tính xác suất thực nghiệm của biến cố "Hai đồng xu đều xuất hiện mặt sấp sau 100 lần tung".
Bài 10 trang 96 Toán 8 Tập 2
Xuân bỏ một số viên bi xanh và đỏ có kích thước và khối lượng giống nhau vào túi. Mỗi lần Xuân lấy ra ngẫu nhiên một viên bi, xem màu của nó rồi trả lại túi. Lặp lại phép thử đó 100 lần, Xuân thấy có 40 lần mình lấy được bi đỏ. Biết rằng trong túi có 9 viên bi xanh, hãy ước lượng xem trong túi có bao nhiêu viên bi đỏ.
Bài 11 trang 96 Toán 8 Tập 2
Một tấm bìa hình tròn được chia thành 6 phần bằng nhau như Hình 1.
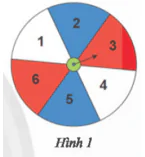
Bạn Thủy quay mũi tên và quan sát xem khi dừng lại mũi tên chỉ vào ô số mấy. Thủy ghi lại kết quả sau 120 lần thí nghiệm ở bảng sau:

a) Tính xác suất thực nghiệm của biến cố "Mũi tên chỉ vào ô có màu trắng".
b) Theo em dự đoán, xác suất mũi tên chỉ vào mỗi ô có bằng nhau hay không?
c) Một người nhận định rằng xác suất mũi tên chỉ vào các ô có màu xanh bằng xác suất mũi tên chỉ vào các ô màu trắng và bằng xác suất mũi tên chỉ vào các ô có màu đỏ. Theo em, kết quả thực nghiệm của bạn Thủy có phù hợp với nhận định đó không?