Giải bài tập Bài 4.14 trang 88 Toán 8 Tập 1 | Toán 8 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 4.14 trang 88 Toán 8 Tập 1. Luyện tập chung chương 4 trang 88. Toán 8 - Kết nối tri thức
Đề bài:
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK // CD, FK // AB.
b) So sánh EF và (AB + CD).
Đáp án và cách giải chi tiết:
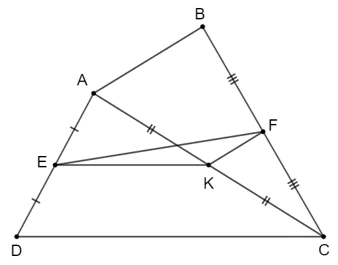
a) Vì E, K lần lượt là trung điểm của AD, AC nên EK là đường trung bình của tam giác ACD suy ra EK // CD.
Vì K, F lần lượt là trung điểm của AC, BC nên KF là đường trung bình của tam giác ABC suy ra KF // AB.
Vậy EK // CD, FK // AB.
b) Vì EK là đường trung bình của tam giác ACD nên EK = CD;
Vì KF là đường trung bình của tam giác ABC nên KF = AB.
Do đó EK + KF = (AB + CD) (1)
Áp dụng bất đẳng thức tam giác vào tam giác KEF, ta có: EF < EK + KF (2)
Từ (1) và (2) ta suy ra EF < (AB + CD).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 4.15 trang 88 Toán 8 Tập 1
Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng .
Bài 4.16 trang 88 Toán 8 Tập 1
Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.
a) Tính độ dài các đoạn thẳng DB và DC.
b) Tính tỉ số diện tích của hai tam giác ABD và ACD.
Bài 4.17 trang 88 Toán 8 Tập 1
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM2 = MN.MK.
