Giải bài tập Bài 10.13 trang 122 Toán 8 Tập 2 | Toán 8 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 10.13 trang 122 Toán 8 Tập 2. Luyện tập chung chương 10 trang 121.. Toán 8 - Kết nối tri thức
Đề bài:
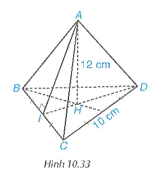
Tính thể tích hình chóp tam giác đều A.BCD có độ dài cạnh đáy bằng 10 cm, chiều cao bằng 12 cm (H.10.33), biết 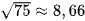 .
.
Đáp án và cách giải chi tiết:
Vì I là trung điểm của BC nên BI = IC = 10 : 2 = 5 cm.
Xét tam giác BID vuông tại I, có
ID2 + BI2 = BD2 (định lí Pythagore).
Suy ra ID2 = BD2 – BI2 = 102 – 52 = 75.
Do đó, ID = 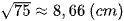 .
.
Diện tích tam giác đáy BCD là:
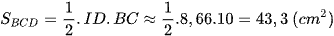
Thể tích hình chóp tam giác đều A.BCD là:
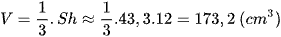
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 10.11 trang 121 Toán 8 Tập 2
Tính thể tích của hình chóp tam giác đều S.ABC, biết diện tích đáy của nó bằng 15,6 cm2, chiều cao bằng 10 cm.
Bài 10.12 trang 122 Toán 8 Tập 2
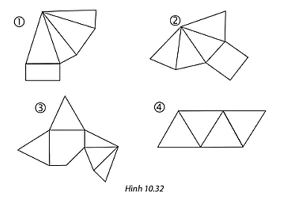
Trong các miếng bìa ở Hình 10.32, miếng bìa nào khi gấp và dán lại thì được một hình chóp tam giác đều, miếng nào thì được một hình chóp tứ giác đều.
Bài 10.14 trang 122 Toán 8 Tập 2
Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.
a) Tính thể tích hình chóp.
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.
