Giải bài tập Hoạt động khám phá 4 trang 61 Toán 12 Tập 1 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động khám phá 4 trang 61 Toán 12 Tập 1. Bài 3. Biểu thức toạ độ của các phép toán vectơ.. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Cho tam giác ABC có A(xA; yA; zA), B(xB; yB; zB), C(xC; yC; zC). Gọi M(xM; yM; zM) là trung điểm của đoạn thẳng AB và G(xG; yG; zG) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ 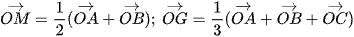 , tìm tọa độ của các điểm M và G.
, tìm tọa độ của các điểm M và G.
Đáp án và cách giải chi tiết:
Ta có 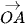 = (xA; yA; zA),
= (xA; yA; zA), 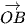 = (xB; yB; zB),
= (xB; yB; zB), 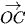 = (xC; yC; zC).
= (xC; yC; zC).
Có 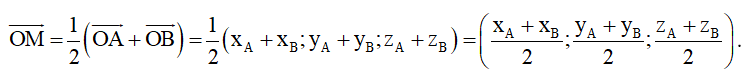
Do đó M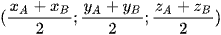 .
.
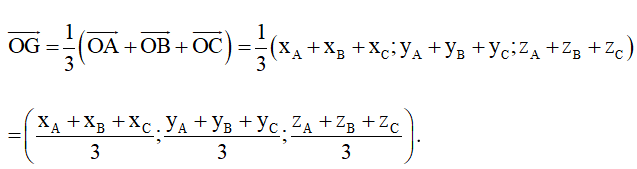
Do đó G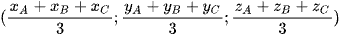 .
.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 64 Toán 12 Tập 1
Bài 1 trang 64 Toán 12 Tập 1: Tính:
a) với
b) với
Bài 2 trang 64 Toán 12 Tập 1
Bài 2 trang 64 Toán 12 Tập 1: Cho hai vectơ Tìm tọa độ của vectơ
Bài 3 trang 64 Toán 12 Tập 1
Bài 3 trang 64 Toán 12 Tập 1: Cho ba điểm A B và C
a) Chứng minh A, B, C là ba đỉnh của một tam giác. Tính chu vi tam giác ABC.
b) Tìm tọa độ trung điểm của các cạnh của tam giác ABC.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
Bài 5 trang 64 Toán 12 Tập 1
Bài 5 trang 64 Toán 12 Tập 1: Cho ba điểm
a) Tìm điểm M trên trục Oy cách đều hai điểm B, C.
b) Tìm điểm N trên mặt phẳng cách đều ba điểm A, B, C.
Bài 6 trang 64 Toán 12 Tập 1
Bài 6 trang 64 Toán 12 Tập 1: Cho các điểm Chứng minh rằng ABCD là hình thang.
Bài 8 trang 64 Toán 12 Tập 1
Bài 8 trang 64 Toán 12 Tập 1: Tính công sinh bởi lực (đơn vị: N) tạo bởi một drone giao hàng (Hình 7) khi thực hiện một độ dịch chuyển (đơn vị: m).

Bài 4 trang 64 Toán 12 Tập 1
Bài 4 trang 64 Toán 12 Tập 1: Cho điểm M Hãy tìm tọa độ của các điểm:
a) M1, M2, M3 lần lượt là hình chiếu vuông góc của M trên các mặt phẳng
b) Gọi lần lượt là các điểm thỏa mãn:
• O là trung điểm của MM';
• vuông góc với mặt phẳng tại điểm H sao cho H là trung điểm của .
• vuông góc và cắt trục Oy tại điểm K sao cho K là trung điểm của
Bài 7 trang 64 Toán 12 Tập 1
Bài 7 trang 64 Toán 12 Tập 1: Cho hình hộp có Tìm tọa độ các đỉnh còn lại của hình hộp.

Hoạt động khởi động trang 58 Toán 12 Tập 1
Trong không gian Oxyz, có thể thực hiện các phép toán vectơ dựa trên tọa độ của chúng tương tự như đã làm trong mặt phẳng Oxy không?
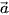 = (x, y, z),
= (x, y, z),  = (x', y', z')
= (x', y', z')
 = ?
= ?

Hoạt động khám phá 1 trang 58 Toán 12 Tập 1
Trong không gian Oxyz, cho hai vectơ  với số thực m.
với số thực m.
a) Biểu diễn từng vectơ 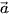 và
và  theo ba vectơ
theo ba vectơ 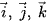 .
.
b) Biểu diễn các vectơ  theo ba vectơ
theo ba vectơ 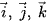 , từ đó suy ra tọa độ của các vectơ
, từ đó suy ra tọa độ của các vectơ  .
.
Thực hành 1 trang 59 Toán 12 Tập 1
Cho ba vectơ  = (2; -5; 3),
= (2; -5; 3),  = (0; 2; -1),
= (0; 2; -1),  = (1; 7; 2).
= (1; 7; 2).
a) Tìm tọa độ của vectơ  .
.
b) Tìm tọa độ của vectơ  .
.
c) Chứng minh  cùng phương với vectơ
cùng phương với vectơ  = (-6; 15; -9).
= (-6; 15; -9).
Vận dụng 1 trang 59 Toán 12 Tập 1
Một thiết bị thăm dò đáy biển đang lặn với vận tốc  = (10; 8; -3) (Hình 1). Cho biết vận tốc của dòng hải lưu của vùng biển là
= (10; 8; -3) (Hình 1). Cho biết vận tốc của dòng hải lưu của vùng biển là 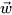 = (3,5; 1; 0).
= (3,5; 1; 0).
a) Tìm tọa độ của vectơ tổng hai vận tốc  và
và  .
.
b) Giả sử thiết bị thăm dò lặn với vận tốc 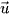 = (7; 2; 0), hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.
= (7; 2; 0), hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.

Hoạt động khám phá 2 trang 59 Toán 12 Tập 1
Cho hai vectơ  .
.
a) Biểu diễn từng vectơ  và
và  theo ba vectơ
theo ba vectơ  .
.
b) Tính các tích vô hướng  .
.
c) Tính tích vô hướng 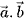 theo tọa độ của hai vectơ
theo tọa độ của hai vectơ  và
và  .
.
Thực hành 2 trang 60 Toán 12 Tập 1
Cho ba vectơ 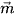 = (-5; 4; 9),
= (-5; 4; 9),  = (2; -7; 0),
= (2; -7; 0), 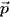 = (6; 3; -4).
= (6; 3; -4).
a) Tính  .
.
b) Tính  .
.
c) Cho  = (1; -2; 0). Vectơ
= (1; -2; 0). Vectơ 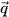 có vuông góc với
có vuông góc với  không?
không?
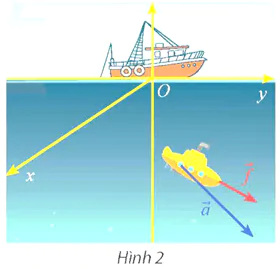
Vận dụng 2 trang 60 Toán 12 Tập 1
Một thiết bị thăm dò đáy biển (Hình 2) được đẩy bởi một lực  = (5; 4; -2) (đơn vị: N) giúp thiết bị thực hiện độ dời
= (5; 4; -2) (đơn vị: N) giúp thiết bị thực hiện độ dời  = (70; 20; -40) (đơn vị: m). Tính công sinh bởi lực
= (70; 20; -40) (đơn vị: m). Tính công sinh bởi lực 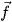 .
.
Hoạt động khám phá 3 trang 60 Toán 12 Tập 1
Cho hai điểm  . Từ biểu thức
. Từ biểu thức  , tìm tọa độ của vectơ
, tìm tọa độ của vectơ 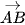 theo tọa độ hai điểm A, B.
theo tọa độ hai điểm A, B.
Thực hành 3 trang 61 Toán 12 Tập 1
Cho ba điểm M(7; −2; 0), N(−9; 0; 4), P(0; −6; 5).
a) Tìm tọa độ của các vectơ  .
.
b) Tính các độ dài MN, NP, MP.
Thực hành 4 trang 62 Toán 12 Tập 1
Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(−3;−1; 0). Tìm tọa độ:
a) Các điểm M', N', P' lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M'N'P'.
Vận dụng 3 trang 62 Toán 12 Tập 1
Cho hình chóp S.ABC có SA (ABC), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ tọa độ như Hình 3, hãy tìm tọa độ:
a) Các điểm A, S, B, C.
b) Trung điểm M của SB và trung điểm N của SC.
c) Trọng tâm G của tam giác SBC.

Thực hành 5 trang 63 Toán 12 Tập 1
Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm tọa độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài cạnh MN và MP.
c) Tính góc M.