Giải bài tập HĐ3 trang 5 Toán 10 Tập 2 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập HĐ3 trang 5 Toán 10 Tập 2. Bài 15: Hàm số. Toán 10 - Kết nối tri thức
Đề bài:
Tính tiền điện
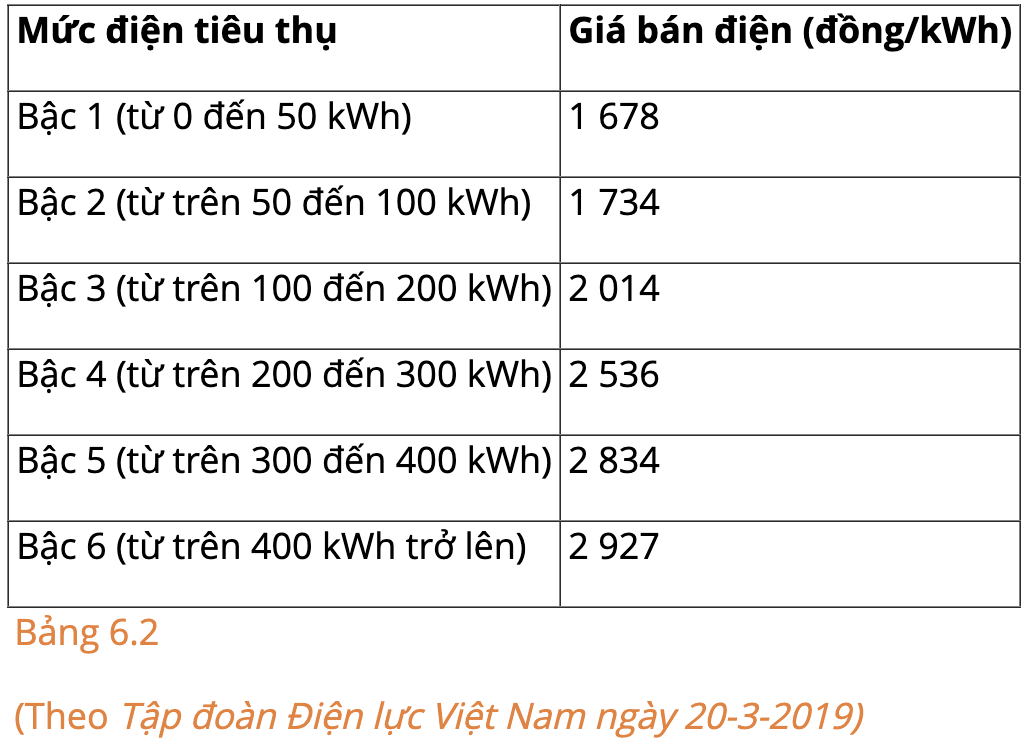
a) Dựa vào Bảng 6.2 về giá bán lẻ điện sinh hoạt, hãy tính số tiền phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3:
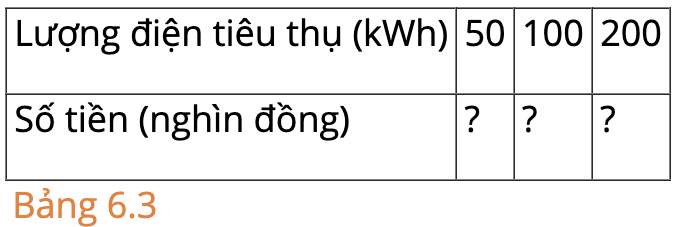
b) Gọi x là lượng điện tiêu thụ (đơn vị kWh) và y là số tiền phải trả tương ứng (đơn vị nghìn đồng). Hãy viết công thức mô tả sự phụ thuộc của y vào x khi 0 ≤ x ≤ 50.
Đáp án và cách giải chi tiết:
a) + Lượng điện tiêu thụ là 50 kWh thì ứng với mức tiêu thụ ở bậc 1 nên số tiền phải trả cho 50 kWh điện này là:
1678 . 50 = 83 900 (đồng) = 83,9 (nghìn đồng).
+ Lượng điện tiêu thụ là 100 kWh thì 50 kWh đầu tính giá ở bậc 1 và 50 kWh sau tính giá ở bậc 2 nên số tiền phải trả cho 100 kWh điện này là:
1678 . 50 + 1734 . 50 = 170 600 (đồng) = 170,6 (nghìn đồng).
+ Lượng điện tiêu thụ là 200 kWh thì 50 kWh đầu tính giá ở bậc 1, 50 kWh tiếp theo tính giá ở bậc 2 và 100 kWh cuối tính giá ở bậc 3 nên số tiền phải trả cho 200 kWh điện này là:
1678 . 50 + 1734 . 50 + 2014 . 100 = 372 000 (đồng) = 372 (nghìn đồng).
Vậy ta điền vào bảng như sau:
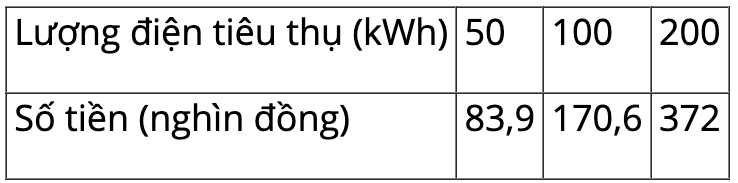
b) x là lượng điện tiêu thụ (đơn vị kWh), y là số tiền phải trả (đơn vị nghìn đồng).
Vì 0 ≤ x ≤ 50 nên lượng điện tiêu thụ thuộc mức điện bậc 1 với giá bán là 1 678 đồng/ 1 kWh hay 1,678 nghìn đồng/ 1 kWh.
Do đó số tiền phải trả cho x kWh là: y = 1,678 . x = 1,678x (nghìn đồng).
Vậy công thức mô tả sự phụ thuộc của y vào x khi 0 ≤ x ≤ 50 là: y = 1,678x.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 6.1 trang 9 Toán 10 Tập 2
Bài 6.1 trang 9 Toán 10 Tập 2: Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x?
a) x + y = 1;
b) y = x2;
c) y2= x;
d) x2 – y2 = 0.
Bài 6.2 trang 9 Toán 10 Tập 2
Bài 6.2 trang 9 Toán 10 Tập 2: Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.
Bài 6.4 trang 9 Toán 10 Tập 2
Bài 6.4 trang 9 Toán 10 Tập 2: Tìm tập xác định và tập giá trị của mỗi hàm số sau:
a) y = 2x + 3;
b) y = 2x2.
Bài 6.5 trang 9 Toán 10 Tập 2
Bài 6.5 trang 9 Toán 10 Tập 2: Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.
a) y = – 2x + 1;
b) .
Mở đầu trang 4 Toán 10 Tập 2
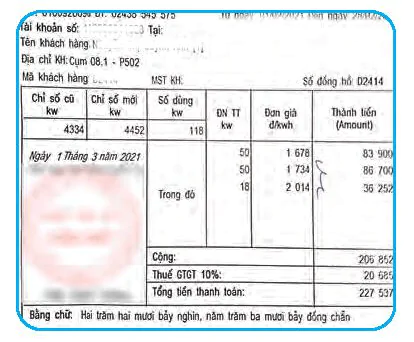
Quan sát hóa đơn tiền điện ở hình bên. Hãy cho biết tổng lượng điện tiêu thụ trong tháng và số tiền phải trả (chưa tính thuế giá trị gia tăng). Có cách nào mô tả sự phụ thuộc của số tiền phải trả vào tổng lượng điện tiêu thụ hay không?
HĐ1 trang 5 Toán 10 Tập 2
Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội:

a) Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời điểm 8 giờ, 12 giờ, 16 giờ.
b) Trong Bảng 6.1, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5?
HĐ2 trang 5 Toán 10 Tập 2
Quan sát Hình 6.1.
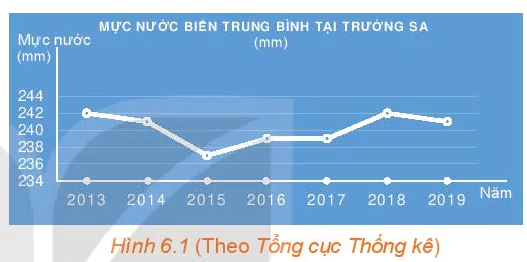
a) Thời gian theo dõi mực nước ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào?
b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất?
Luyện tập 1 trang 6 Toán 10 Tập 2
a) Hãy cho biết Bảng 6.4 có cho ta một hàm số hay không. Nếu có, tìm tập xác định và tập giá trị của hàm số đó.

b) Trở lại HĐ2, ta có hàm số cho bằng biểu đồ. Hãy cho biết giá trị của hàm số tại x = 2018.
c) Cho hàm số y = f(x) = – 2x2. Tính f(1); f(2) và tìm tập xác định, tập giá trị của hàm số này.
HĐ4 trang 7 Toán 10 Tập 2
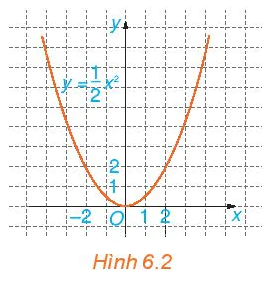
Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số 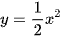 .
.
(0; 0), (2; 2), (– 2; 2), (1; 2), (– 1; 2).
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
Luyện tập 2 trang 7 Toán 10 Tập 2
a) Dựa vào đồ thị của hàm số 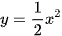 (H.6.2), tìm x sao cho y = 8.
(H.6.2), tìm x sao cho y = 8.
b) Vẽ đồ thị của các hàm số y = 2x + 1 và y = 2x2 trên cùng một mặt phẳng tọa độ.
Vận dụng 1 trang 7 Toán 10 Tập 2
Nếu lượng điện tiêu thụ từ 50 đến 100 kWh (50 < x ≤ 100) thì công thức liên hệ giữa y và x đã thiết lập ở HĐ3 không còn đúng nữa.
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là:
y = 1,678 . 50 + 1,734(x – 50) = 83,9 + 1,734(x – 50) hay y = 1,734x – 2,8 (nghìn đồng).
Vậy trên tập xác định D = (50; 100], hàm số y mô tả số tiền phải thanh toán có công thức là y = 1,734x – 2,8; tập giá trị của nó là (83,9; 170,6].
Hãy vẽ đồ thị ở Hình 6.3 vào vở rồi vẽ tiếp đồ thị của hàm số y = 1,734x – 2,8 trên tập D = (50; 100].
HĐ5 trang 8 Toán 10 Tập 2
Cho các hàm số y = – x + 1 và y = x. Tính giá trị y theo giá trị x để hoàn thành bảng sau:
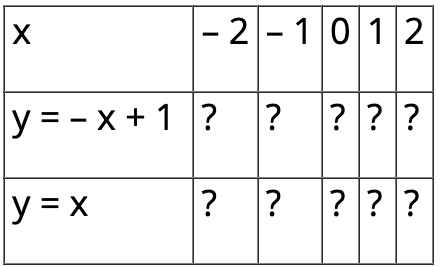
Khi giá trị x tăng, giá trị y tương ứng của mỗi hàm số y = = – x + 1 và y = x tăng hay giảm?
HĐ6 trang 8 Toán 10 Tập 2
Quan sát đồ thị của hàm số y = f(x) = – x2 trên R (H.6.5).
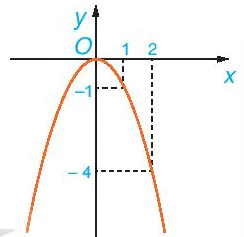
Hỏi:
a) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng (– ∞; 0)?
b) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng (0; + ∞)?
Luyện tập 3 trang 9 Toán 10 Tập 2
Vẽ đồ thị của các hàm số y = 3x + 1 và y = – 2x2. Hãy cho biết:
a) Hàm số y = 3x + 1 đồng biến hay nghịch biến trên R.
b) Hàm số y = – 2x2 đồng biến hay nghịch biến trên mỗi khoảng: (– ∞; 0) và (0; + ∞).
Vận dụng 2 trang 9 Toán 10 Tập 2
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.

a) Tính số tiền phải trả khi di chuyển 25 km.
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào?
Bài 6.3 trang 9 Toán 10 Tập 2
Bài 6.3 trang 9 Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:
a) 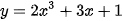 ;
;
b) 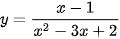
c) 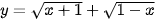 .
.
Bài 6.6 trang 9 Toán 10 Tập 2
Bài 6.6 trang 9 Toán 10 Tập 2: Giá thuê xe ô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và 900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe.
a) Viết công thức của hàm số T = T(x).
b) Tính T(2), T(3), T(5) và cho biết ý nghĩa của mỗi giá trị này.