Giải bài tập Bài 5.26 trang 90 Toán 10 Tập 1 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 5.26 trang 90 Toán 10 Tập 1. Bài tập cuối chương 5. Toán 10 - Kết nối tri thức
Đề bài:
Bài 5.26 trang 90 Toán 10 Tập 1: Tỉ lệ trẻ em suy dinh dưỡng (tính theo cân nặng tương ứng với độ tuổi) của 10 tỉnh thuộc Đồng bằng sông Hồng được cho như sau:
5,5 13,8 10,2 12,2 11,0 7,4 11,4 13,1 12,5 13,4.
a) Tính số trung bình, trung vị, khoảng biến thiên và độ lệch chuẩn của mẫu số liệu trên.
b) Thực hiện làm tròn đến hàng đơn vị cho cá giá trị trong mẫu số liệu. Sai số tuyệt đồi của phép làm tròn này không vượt quá bao nhiêu?
Đáp án và cách giải chi tiết:
a) Số trung bình của mẫu số liệu là:
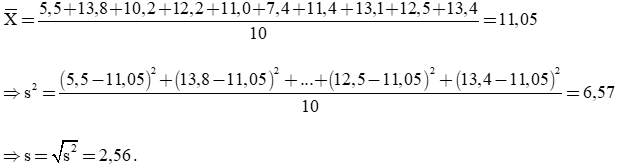
Sắp xếp dãy số liệu theo thứ tự không giảm, ta được:
5,5; 7,4; 10,2; 11,0; 11,4; 12,2; 12,5; 13,1; 13,4; 13,8.
Vì n = 10 là số chẵn nên số trung vị là trung bình cộng của hai giá trị chính giữa:
(11,4 + 12,2) : 2 = 11,8.
Ta có giá trị lớn nhất của số liệu là 13,8 và giá trị nhỏ nhất là 5,5. Khi đó khoảng biến thiên là: R = 13,8 – 5,5 = 8,3.
b) Thực hiện làm tròn đến hàng đơn vị cho các giá trị trong mẫu số liệu, ta được:
5,5; 7,4; 10,2; 11,0; 11,4; 12,2; 12,5; 13,1; 13,4; 13,8.
6 ; 7; 10; 11; 11; 12; 13; 13; 13; 14.
Sai số của phép làm tròn này không vượt quá
|
a |
||
|
6 |
5,5 |
0,5 |
|
7 |
7,4 |
0,4 |
|
10 |
10,2 |
0,2 |
|
11 |
11,0 |
0 |
|
11 |
11,4 |
0,4 |
|
12 |
12,2 |
0,2 |
|
13 |
12,5 |
0,5 |
|
13 |
13,1 |
0,1 |
|
13 |
13,4 |
0,4 |
|
14 |
13,8 |
0,2
|
Sai số tuyệt đối của phép làm tròn này không vượt quá 0,5.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 5.17 trang 89 Toán 10 Tập 1
Bài 5.17 trang 89 Toán 10 Tập 1: Khi cân một bao gạo bằng một cân treo với thang chia 0,2kg thì độ chính xác d là:
A. 0,1 kg.
B. 0,2kg.
C. 0,3 kg.
D. 0,4kg.
Bài 5.18 trang 89 Toán 10 Tập 1
Bài 5.18 trang 89 Toán 10 Tập 1: Trong hai mẫu số liệu, mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn là đúng hay sai?
A. Đúng
B. Sai
Bài 5.19 trang 89 Toán 10 Tập 1
Bài 5.19 trang 89 Toán 10 Tập 1: Có 25% giá trị của mẫu số liệu nằm giữa Q1 và Q3, đúng hay sai?
A. Đúng.
B. Sai.
Bài 5.20 trang 89 Toán 10 Tập 1
Bài 5.20 trang 89 Toán 10 Tập 1: Số đặc trưng nào sau đây đo độ phân tán của mẫu số liệu?
A. Số trung bình.
B. Mốt.
C. Trung vị.
D. Độ lệch chuẩn.
Bài 5.21 trang 89 Toán 10 Tập 1
Bài 5.21 trang 89 Toán 10 Tập 1: Điểm trung bình môn học kì I một số môn học của An là: 8; 9; 7; 6; 5; 7; 3. Nếu An được cộng thêm mỗi môn 0,5 điểm chuyên cần thì các số đặc trưng nào sau đây của mẫu số liệu không thay đổi?
Bài 5.22 trang 89 Toán 10 Tập 1
Bài 5.22 trang 89 Toán 10 Tập 1: Lương khởi điểm của 5 sinh viên vừa tốt nghiệp tại một trường học (đơn vị: triệu đồng) là:
3,5 9,2 9,2 9,5 10,5.
a) Giải thích tại sao nên dùng trung vị để thể hiện mức lương khởi điểm của sinh viên tốt nghiệp từ trường đại học này.
b) Nên dùng khoảng biến thiên hay khoảng tứ phân vị để đo độ phân tán.
Bài 5.23 trang 89 Toán 10 Tập 1
Bài 5.23 trang 89 Toán 10 Tập 1: Điểm Toán và Tiếng Anh của 11 học sinh lớp 10 được cho trong bảng sau:
Hãy so sánh mức độ học đều của học sinh môn Tiếng Anh và môn Toán thông qua các số đặc trưng: khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn.
Bài 5.24 trang 90 Toán 10 Tập 1
Bài 5.24 trang 90 Toán 10 Tập 1: Bảng sau cho biết dân số của các tỉnh/thành phố Đồng bằng Bắc Bộ năm 2018 (đơn vị triệu người).
a) Tìm số trung bình và trung vị của mẫu số liệu trên.
b) Giải thích tại sao số trung bình và trung vị lại có sự sai khác nhiều.
c) Nên sử dụng số trung bình hay trung vị đại diện cho dân số các tỉnh thuộc Đồng bằng Bắc Bộ?
Bài 5.25 trang 90 Toán 10 Tập 1
Bài 5.25 trang 90 Toán 10 Tập 1: Hai mẫu số liệu sau đây cho biết số lượng trường Trung học phổ thông ở mỗi tỉnh thuộc Đồng bằng Bắc Bộ?
Đồng bằng sông Hồng: 187 34 35 46 54 57 37 39 23 57 27.
Đồng bằng sông Cửu Long: 33 34 33 29 24 39 42 24 23 19 24 15 26.
a) Tính số trung bình, trung vị, các tứ phân vị, mốt, khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn cho mỗi mẫu số liệu trên.
b) Tại sao số trung bình của hai mẫu số liệu có sự sai khác nhiều trong khi trung vị thì không?
c) Tại sao khoảng biến thiên và độ lệch chuẩn của hai mẫu số liệu khác nhau nhiều trong khi khoảng tứ phân vị thì không?