Giải bài tập Thực hành 1 trang 89 Toán 12 Tập 1 | SGK Toán 12 - Chân trời sáng tạo

Hướng dẫn giải chi tiết từng bước bài tập Thực hành 1 trang 89 Toán 12 Tập 1. Bài 1. Vẽ đồ thị hàm số bằng phần mềm Geogebra 87.. SGK Toán 12 - Chân trời sáng tạo

Đề bài:

Thực hành 1 trang 89 Toán 12 Tập 1: Vẽ đồ thị các hàm số bậc ba sau:

a) $y = x^{3};$ b) $y = x^{3} - 3 x;$

c) $y = - x^{3} + 3 x;$ d) $y = x^{3} - 3 x + 2 .$

Đáp án và cách giải chi tiết:

a) $y = x^{3}$

- Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

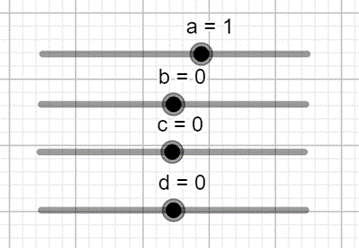
- Nhập hàm số $y = x^{3}$ vào vùng nhập lệnh.

- Ta được đồ thị như hình vẽ

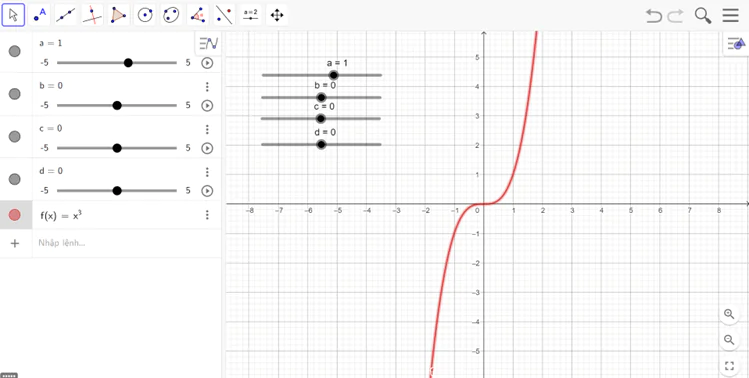
- Nhận xét:

Hàm số đồng biến trên khoảng $(0; + \infty)$ và nghịch biến trên khoảng $(- \infty; 0) .$

Hàm số đã cho không có cực trị.

Đồ thị có tâm đối xứng là $(0; 0) .$

b) $y = x^{3} - 3 x$

- Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

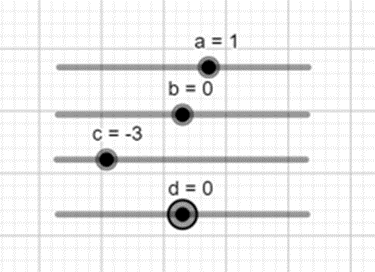
- Nhập hàm số $y = x^{3} - 3 x$ vào vùng nhập lệnh.

- Ta được đồ thị như hình vẽ

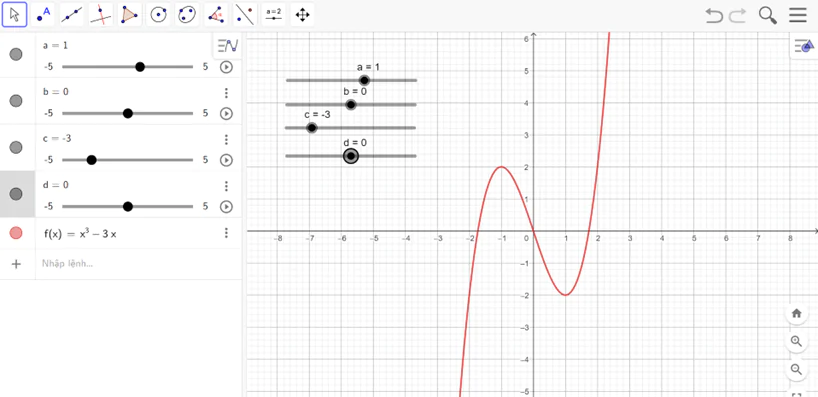
Nhận xét:

Hàm số đồng biến trên các khoảng $(- \infty; - 1)$ và $(1; + \infty) .$

Hàm số nghịch biến trên khoảng $(- 1; 1) .$

Điểm cực đại là $(- 1; 2),$ điểm cực tiểu là $(1; - 2) .$

Đồ thị hàm số có tâm đối xứng là $(0; 0) .$

c) $y = - x^{3} + 3 x$

- Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

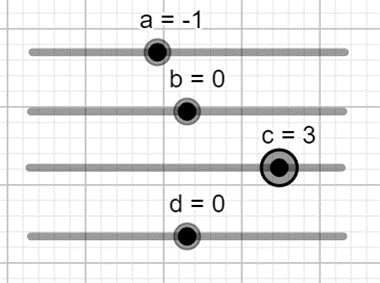
- Nhập hàm số $y = - x^{3} + 3 x$ vào vùng nhập lệnh.

- Ta được đồ thị như hình vẽ

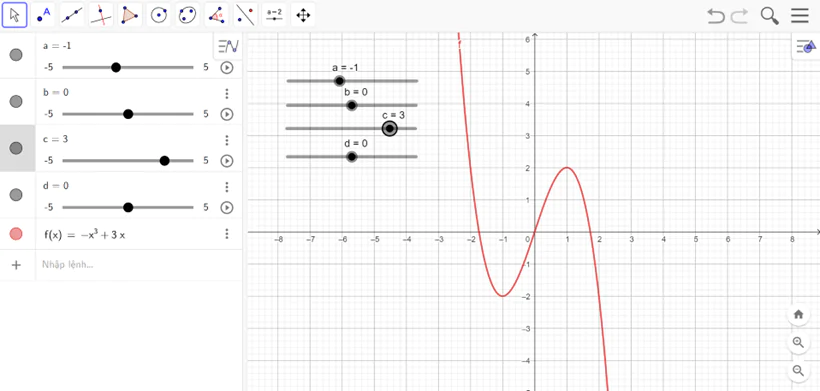
Nhận xét:

Hàm số nghịch biến trên các khoảng $(- \infty; - 1)$ và $(1; + \infty) .$

Hàm số đồng biến trên khoảng $(- 1; 1) .$

Điểm cực đại là $(1; 2),$ điểm cực tiểu là $(- 1; - 2) .$

Đồ thị hàm số có tâm đối xứng là $(0; 0) .$

d) $y = x^{3} - 3 x + 2$

- Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

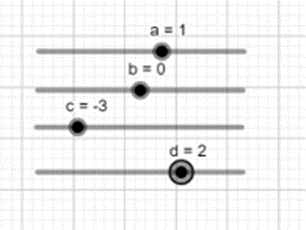
- Nhập hàm số $y = x^{3} - 3 x + 2$ vào vùng nhập lệnh.

- Ta được đồ thị như hình vẽ

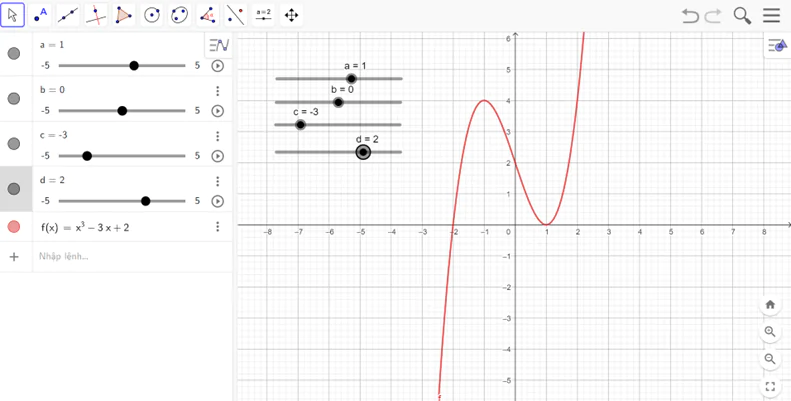
Nhận xét:

Hàm số đồng biến trên các khoảng $(- \infty; - 1)$ và $(1; + \infty) .$

Hàm số nghịch biến trên khoảng $(- 1; 1) .$

Điểm cực đại là $(- 1; 4),$ điểm cực tiểu là $(1; 0) .$

Đồ thị hàm số có tâm đối xứng là $(0; 2) .$

Nguồn: loigiaitoan.com

Tổng số đánh giá:

Xếp hạng: / 5 sao

Bài tập liên quan:

Thực hành 2 trang 89 Toán 12 Tập 1

Thực hành 2 trang 89 Toán 12 Tập 1: Vẽ đồ thị các hàm số sau:

a) $y = \frac{x + 1}{x - 1};$ b) $y = \frac{- x - 1}{x - 1} .$

Xem cách giải chi tiết

Thực hành 3 trang 90 Toán 12 Tập 1

Thực hành 3 trang 90 Toán 12 Tập 1: Vẽ đồ thị các hàm số sau:

Xem cách giải chi tiết

Giải bài tập SGK Toán 12 - Chân trời sáng tạo

Chương 1. Ứng dụng đạo hàm để khảo sát hàm số

Bài 1. Tính đơn điệu và cực trị của hàm số.

Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Bài 3. Đường tiệm cận của đồ thị hàm số.

Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản.

Bài tập cuối chương I.

Chương 2. Vectơ và hệ tọa độ trong không gian

Bài 1. Vectơ và các phép toán trong không gian.

Bài 2. Toạ độ của vectơ trong không gian.

Bài 3. Biểu thức toạ độ của các phép toán vectơ.

Bài tập cuối chương 2.

Chương 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm

Bài 1. Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm.

Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm.

Bài tập cuối chương 3.

Hoạt động thực hành và trải nghiệm

Bài 1. Vẽ đồ thị hàm số bằng phần mềm Geogebra 87.

Bài 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay 91.

Chương 4. Nguyên hàm. Tích phân.

Bài 1. Nguyên hàm.

Bài 2. Tích phân.

Bài 3. Ứng dụng hình học của tích phân.

Bài tập cuối chương 4.

Chương 5. Phương trình mặt phẳng, đường thẳng, mặt cầu

Bài 1. Phương trình mặt phẳng

Bài 2. Phương trình đường thẳng trong không gian

Bài 3. Phương trình mặt cầu

Bài tập cuối chương 5

Chương 6. Xác suất có điều kiện

Bài 1. Xác suất có điều kiện

Bài 2. Công thức xác suất toàn phần và công thức Bayes.

Bài tập cuối chương 6

Hoạt động thực hành và trải nghiệm

Bài 1. Tính giá trị gần đúng tích phân bằng máy tính cầm tay.

Bài 2. Minh hoạ và tính tích phân bằng phần mềm GeoGebra.

Bài 3. Sử dụng phần mềm GeoGebra để biểu diễn hình học toạ độ trong không gian.

Từ điển Phương Trình Hoá Học

CaO+P2O5 → Ca3(PO4)2 Pb(NO3)2 → NO2+O2+PbO C2H2 → C4H4 CaF2+H2SO4+SiO2 → H2O+CaSO4+SiF4 O2+Na2B4O7 → NaBO2+B2O3

Công Thức Vật Lý

Các dạng dao động điện từ đặc biệt - vật lý 12 Chiết suất môi trường theo bước sóng ánh sáng - vật lý 12