Giải bài tập Hoạt động 3 trang 73 Toán lớp 10 Tập 1 | Toán 10 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động 3 trang 73 Toán lớp 10 Tập 1. Bài 2: Giải tam giác. Tính diện tích tam giác. Toán 10 - Cánh diều
Đề bài:
Cho tam giác ABC có BC = a,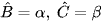 
. Viết công thức tính AB và AC theo a, α, β.
Đáp án và cách giải chi tiết:
Tam giác ABC có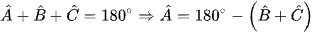 
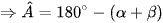
⇒ sinA = sin(180° – (α + β)) = sin(α + β).
Áp dụng định lí sin trong tam giác ABC ta có:
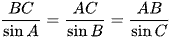
Suy r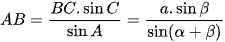a: 
và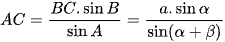 
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 77 Toán lớp 10 Tập 1
Bài 1 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = 12, CA = 15, . Tính:
a) Độ dài cạnh AB;
b) Số đo các góc A, B;
c) Diện tích tam giác ABC.
Bài 2 trang 77 Toán lớp 10 Tập 1
Bài 2 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 5, BC = 7, . Tính độ dài cạnh AC.
Bài 3 trang 77 Toán lớp 10 Tập 1
Bài 3 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 100, ; . Tính:
a) Độ dài các cạnh AC, BC;
b) Diện tích tam giác ABC.
Bài 4 trang 77 Toán lớp 10 Tập 1
Bài 4 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 12, AC = 15, BC = 20. Tính:
a) Số đo các góc A, B, C;
b) Diện tích tam giác ABC.
Bài 5 trang 77 Toán lớp 10 Tập 1
Bài 5 trang 77 Toán lớp 10 Tập 1: Tính độ dài cạnh AB trong mỗi trường hợp sau:
Bài 6 trang 77 Toán lớp 10 Tập 1
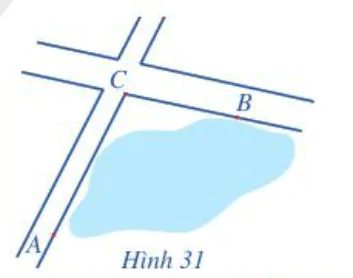
Bài 6 trang 77 Toán lớp 10 Tập 1: Để tính khoảng cách giữa hai địa điểm A và B mà không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Bài 7 trang 77 Toán lớp 10 Tập 1
Bài 7 trang 77 Toán lớp 10 Tập 1: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45° và 75°. Biết khoảng cách giữa hai bị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Câu hỏi khởi động trang 72 Toán lớp 10 Tập 1
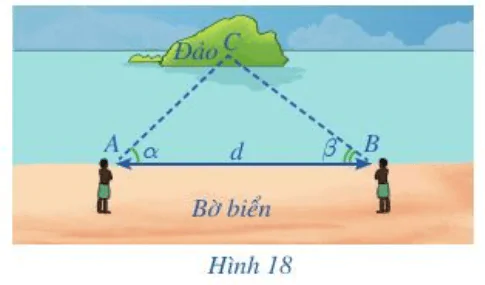
Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để do khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,…) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:
Từ vị trí A, đo góc nghiêng α so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng β so với bờ biển tới vị trí C đã chọn (Hình 18). Bằng cách giải tam giác BAC, họ tính được khoảng cách AC.
Giải tam giác được hiểu như thế nào?
Hoạt động 1 trang 72 Toán lớp 10 Tập 1
Cho tam giác ABC có AB = c, AC = b,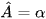 
.
Viết công thức tính BC theo b, c, α.
Hoạt động 2 trang 73 Toán lớp 10 Tập 1
Cho tam giác ABC có AB = c, AC = b, BC = a. Viết công thức tính cos A theo a, b, c.
Hoạt động 4 trang 73 Toán lớp 10 Tập 1
Cho tam giác ABC có AB = c, AC = b, BC = a. Kẻ đường cao BH.
a) Tính BH theo c và sin A.
b) Tính diện tích S của tam giác ABC theo b, c, và sin A.
Luyện tập 1 trang 74 Toán lớp 10 Tập 1
Cho tam giác ABC có AB = 12;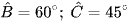 
. Tính diện tích của tam giác ABC.
Hoạt động 5 trang 75 Toán lớp 10 Tập 1
Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24).
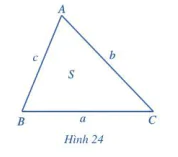
a) Từ định lí côsin, chứng tỏ rằng:
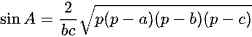, ở đó 
.
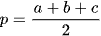b) Bằng cách sử dụng công thức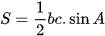 
, hãy chứng tỏ rằng: 
.
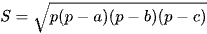Luyện tập 2 trang 76 Toán lớp 10 Tập 1
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34°, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?