Giải bài tập Bài 3 trang 76 Toán 11 Tập 2 | Toán 11 - Cánh diều

Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 76 Toán 11 Tập 2. Bài tập cuối chương 7. Toán 11 - Cánh diều

Đề bài:

Tìm đạo hàm của mỗi hàm số sau:

a) y = (x² + 2x)(x³ – 3x); b) 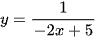$y = \frac{1}{- 2 x + 5}$ c) $y = \sqrt{4 x + 5}$

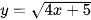d) y = sinxcosx; e) y = xe^x; g) y = ln²x.

Đáp án và cách giải chi tiết:

a) Xét hàm số y = (x² + 2x)(x³ – 3x), ta có:

y' = (x² + 2x)'(x³ – 3x) + (x² + 2x)(x³ – 3x)'

= (2x + 2)(x³ – 3x) + (x² + 2x)(3x² – 3)

= 2x⁴ – 6x² + 2x³ – 6x + 3x⁴ – 3x² + 6x³ – 6x

= 5x⁴ + 8x³ – 9x² – 12x.

b) Xét hàm số 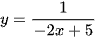$y = \frac{1}{- 2 x + 5}$ , ta có:

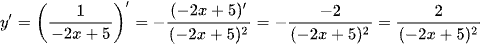
$y' = {(\frac{1}{- 2 x + 5})}^{'} = - \frac{(- 2 x + 5)'}{{(- 2 x + 5)}^{2}} = - \frac{- 2}{{(- 2 x + 5)}^{2}} = \frac{2}{{(- 2 x + 5)}^{2}}$

c) Xét hàm số 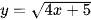$y = \sqrt{4 x + 5}$ , ta có:

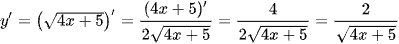
$y' = (\sqrt{4 x + 5})' = \frac{(4 x + 5)'}{2 \sqrt{4 x + 5}} = \frac{4}{2 \sqrt{4 x + 5}} = \frac{2}{\sqrt{4 x + 5}}$

d) Xét hàm số y = sinxcosx

Cách 1.

y' = (sinxcosx)' = (sinx)'.cosx + sinx.(cosx)'

= cosx.cosx + sinx.(–sinx)

= cos²x – sin²x = cos2x.

Cách 2.

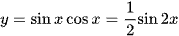
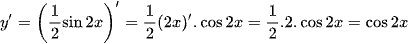
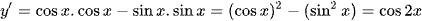
Ta có $y = s i n x c o s x = \frac{1}{2} \sin 2 x .$ $y = sinx . cosx = \frac{1}{2} \sin 2 x$

Suy ra $y' = {(\frac{1}{2} \sin 2 x)}^{'} = \frac{1}{2} (2 x)' . \cos 2 x = \frac{1}{2} . 2 . \cos 2 x = \cos 2 x$

$y' = cosx . cosx - sinx . sinx = {(cosx)}^{2} - {(sinx)}^{2} = \cos 2 x$

e) Xét hàm số y = xe^x, ta có:

y' = (xe^x)' = (x)' . e^x + x . (e^x)' = e^x + xe^x.

g) Xét hàm số y = ln²x, ta có:

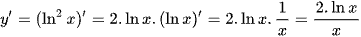
$y' = (\ln^{2} x)' = 2 lnx . (lnx)' = 2 lnx . \frac{1}{x} = \frac{2 lnx}{x}$

Nguồn: loigiaitoan.com

Tổng số đánh giá:

Xếp hạng: / 5 sao

Các công thức liên quan:

Công thức đạo hàm

Công thức đạo hàm hay và đầy đủ nhất, công thức đạo hàm tính nhanh, công thức đạo hàm hàm đa thức, hàm căn thức, hàm phân thức hữu tỉ, hàm lượng giác, hàm mũ, hàm loga, hàm hợp

Xem chi tiết công thức

Bài tập liên quan:

Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động $x = 4 \cos (πt - \frac{2 π}{3}) + 3$ , trong đó t tính bằng giây và x tính bằng centimet.

a) Tìm vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm t (s).

b) Tìm thời điểm mà vận tốc tức thời của con lắc bằng 0.

Xem cách giải chi tiết

Bài 5 trang 76 Toán 11 Tập 2

Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức v(t) = 2t + t², trong đó t > 0, t tính bằng giây và v(t) tính bằng m/s. Tìm gia tốc tức thời của chất điểm:

a) Tại thời điểm t = 3 (s);

b) Tại thời điểm mà vận tốc của chất điểm bằng 8 m/s.

Xem cách giải chi tiết

Bài 4 trang 76 Toán 11 Tập 2

Tìm đạo hàm cấp hai của mỗi hàm số sau:

a) y = 2x4 – 3x3 + 5x2; b) 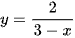$y = \frac{2}{3 - x}$ c) y = sin2xcosx;

d) y = e–2x+3; e) y = ln(x + 1); g) y = ln(ex + 1).

Xem cách giải chi tiết

Bài 2 trang 76 Toán 11 Tập 2

Cho u = u(x), v = v(x) là hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

{(\frac{u}{v})}^{'} = \frac{u'}{v'}

với v = v(x) ≠ 0, v' = v'(x) ≠ 0.

{(\frac{u}{v})}^{'} = \frac{u' v - uv'}{v}

với v = v(x) ≠ 0.

{(\frac{u}{v})}^{'} = \frac{u' v - uv'}{v^{2}}

với v = v(x) ≠ 0.

{(\frac{u}{v})}^{'} = \frac{u' v - uv'}{v'}

với v = v(x) ≠ 0, v' = v' (x) ≠ 0.

Xem cách giải chi tiết

Bài 1 trang 76 Toán 11 Tập 2

Cho u = u(x), v = v(x) là hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

A. (uv)' = u'v'.

B. (uv)' = uv'.

C. (uv)' = u'v.

D. (uv)' = u'v + uv'.

Xem cách giải chi tiết

Từ điển Phương Trình Hoá Học

(CH3COO)2Ca → CaCO3+CH3COCH3 Ca(OH)2+H3PO4 → H2O+CaHPO4 HCl+Fe(OH)2 → FeCl2+H2O CaF2+H2SO4+SiO2 → H2O+CaSO4+SiF4 O2+Na2B4O7 → NaBO2+B2O3

Công Thức Vật Lý

Điều kiện xảy ra phản xạ toàn phần của chùm sáng - vật lý 12 Thời gian nóng chảy khối thép - vật lý 12

Giải bài tập Bài 3 trang 76 Toán 11 Tập 2 | Toán 11 - Cánh diều

Đề bài:

Đáp án và cách giải chi tiết:

Các công thức liên quan:

Công thức đạo hàm

Bài tập liên quan:

Bài 6 trang 76 Toán 11 Tập 2

Bài 5 trang 76 Toán 11 Tập 2

Bài 4 trang 76 Toán 11 Tập 2

Bài 2 trang 76 Toán 11 Tập 2

Bài 1 trang 76 Toán 11 Tập 2

Giải bài tập Toán 11 - Cánh diều

Chương 1: Hàm số lượng giác và phương trình lượng giác

Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

Bài 2: Các phép biến đổi lượng giác

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Chương 2: Dãy số. Cấp số cộng. Cấp số nhân

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân

Bài tập cuối chương 2

Chương 3: Giới hạn. Hàm số liên tục

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Hoạt động thực hành và trải nghiệm - Tập 1

Chủ đề 1: Một số hình thức đầu tư tài chính

Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

Bài 1: Đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song trong không gian

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song

Bài 5: Hình lăng trụ và hình hộp

Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian

Bài tập cuối chương 4

Chương 5: Một số yếu tố thống kê và xác suất

Bài 1: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm

Bài 2: Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất

Bài tập cuối chương 5

Chương 6: Hàm số mũ và hàm số lôgarit

Bài 1: Phép tính lũy thừa với số mũ thực

Bài 2: Phép tính lôgarit

Bài 3: Hàm số mũ. Hàm số lôgarit

Bài 4: Phương trình, bất phương trình mũ và lôgarit

Bài tập cuối chương 6

Chương 7: Đạo hàm

Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Bài 2: Các quy tắc tính đạo hàm

Bài 3: Đạo hàm cấp hai

Bài tập cuối chương 7

Chương 8: Quan hệ vuông góc trong không gian. Phép chiếu vuông góc

Bài 1: Hai đường thẳng vuông góc

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 4: Hai mặt phẳng vuông góc

Bài 5: Khoảng cách

Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

Bài tập cuối chương 8

Hoạt động thực hành và trải nghiệm - Tập 2

Chủ đề 2: Tính thể tích một số hình khối trong thực tiễn

Từ điển Phương Trình Hoá Học

Công Thức Vật Lý