Giải bài tập Bài 8 trang 125 Toán 9 Tập 1: | Toán 9 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 8 trang 125 Toán 9 Tập 1:. Bài tập cuối chương 5. Toán 9 - Cánh diều
Đề bài:
Logo ở Hình 95 có dạng một hình quạt tròn bán kính 8 cm và góc ở tâm bằng 60°. Tính diện tích mỗi hình sau (theo đơn vị centimét vuông và làm tròn kết quả đến hàng phần mười).

a) Toàn bộ logo;
b) Phần logo màu đỏ có dạng hình viên phân.
Đáp án và cách giải chi tiết:
a) Diện tích toàn bộ phần logo có dạng hình quạt tròn là:
b) 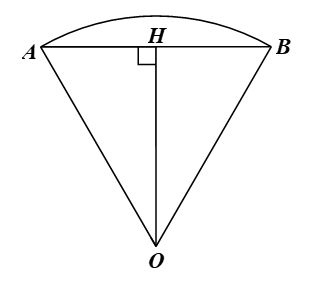
Kẻ OH ⊥ AB.
Xét ∆OAB có OA = OB = R và nên ∆OAB là tam giác đều. Do đó
Xét ∆OHA vuông tại H, ta có: OH = OA.sin = OA.sin60o (cm).
Diện tích phần logo màu xanh có dạng tam giác OAB là:
S1 = OA.OH = OA.OA.sin60o = .8.8.sin60o = 16 (cm2) 27,7 (cm2).
Diện tích phần logo màu đỏ có dạng hình viên phân là:
S2 = S – S1 ≈ 33,5 – 27,7 = 5,8 (cm2).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 124 Toán 9 Tập 1:
Trong Hình 92, cho các điểm A, B, C, D, E thuộc đường tròn (O).

a) Số đo góc BOC là
Α. α.
B. 2α.
C. 180° – α.
D. 180° – 2α.
b) Số đo góc BDC là
Α. α.
B.
C. 180° – α.
D. 180° –
c) Số đo góc BEC là
Α. α.
B. 2α.
C. 180° – α.
D. 360° – α.
Bài 2 trang 124 Toán 9 Tập 1:
a) Độ dài cung tròn có số đo 30° của đường tròn bán kính R là:
A.
B.
C. 30πR.
D.
b) Diện tích của hình quạt tròn tâm O, bán kính R, cung có số đo 45° là:
A.
B.
C.
D. 
Bài 3 trang 124 Toán 9 Tập 1:
Cho hình vuông ABCD cạnh r và đường tròn (C; r). Giả sử M là một điểm nằm trên đường tròn (C; r) sao cho điểm M nằm trong hình vuông ABCD. Tiếp tuyến của đường tròn (C; r) tại tiếp điểm M cắt các đoạn thẳng AB, AD lần lượt tại N, P. Chứng minh:
a) Các đường thẳng NB, PD là các tiếp tuyến của đường tròn (C; r).
b)
Bài 4 trang 124 Toán 9 Tập 1:
Chứng minh trong một đường tròn:
a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy;
b) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy;
c) Hai dây bằng nhau thì cách đều tâm;
d) Hai dây cách đều tâm thì bằng nhau.
Bài 5 trang 124 Toán 9 Tập 1:
Cho hai đường tròn (I; r) và (K; R) tiếp xúc ngoài với nhau tại P với R ≠ r, đường thẳng a lần lượt tiếp xúc với (I; r) và (K; R) tại A và B, a cắt KI tại O. Đường thẳng qua P vuông góc với IK cắt đường thẳng a tại M. Chứng minh:
a)
b) AB = 2MP;
c)
Bài 6 trang 125 Toán 9 Tập 1:
Mặt đĩa CD ở Hình 93 có dạng hình vành khuyên giới hạn bởi hai đường tròn có bán kính lần lượt là 1,5 cm và 6 cm. Hình vành khuyên đó có diện tích bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?

Bài 7 trang 125 Toán 9 Tập 1:
Hình 94 mô tả mảnh vải có dạng một phần tư hình vành khuyên, trong đó hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 3 dm và 5 dm. Diện tích của mảnh vải đó bằng bao nhiêu decimét vuông (làm tròn kết quả đến hàng phần mười)?

Bài 9 trang 125 Toán 9 Tập 1:
Hình 96 biểu diễn vùng biển được chiếu sáng bởi một hải đăng có dạng một hình quạt tròn với bán kính 18 dặm, cung AmB có số đo 245°.
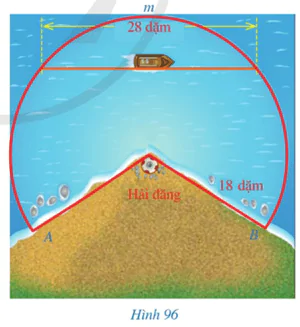
a) Hãy tính diện tích vùng biển có thể nhìn thấy ánh sáng từ hải đăng theo đơn vị kilômét vuông (lấy 1 dặm = 1 609 m và làm tròn kết quả đến hàng đơn vị).
b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn, bán kính là 18 dặm. Tính khoảng cách nhỏ nhất từ con thuyền đến hải đăng (theo đơn vị dặm và làm tròn kết quả đến hàng đơn vị).