Giải bài tập Bài 6 trang 100 Toán 9 Tập 1: | Toán 9 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 6 trang 100 Toán 9 Tập 1:. Bài 1. Đường tròn. Vị trí tương đối của hai đường tròn. Toán 9 - Cánh diều
Đề bài:
Cho đường tròn (O; R) và dây AB khác đường kính. Gọi M là trung điểm của AB.
a) Đường thẳng OM có phải là đường trung trực của đoạn thẳng AB hay không? Vì sao?
b) Tính khoảng cách từ điểm O đến đường thẳng AB, biết R = 5 cm, AB = 8 cm.
Đáp án và cách giải chi tiết:
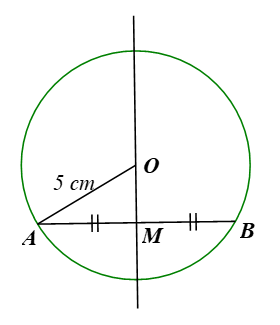
a) Vì AB là dây cung của đường kính (O; R) nên ta có OA = OB = R.
Khi đó, O nằm trên đường trung trực của AB.
Lại có M là trung điểm của AB nên M cũng nằm trên đường trung trực của AB.
Do đó OM là đường trung trực của đoạn thẳng AB.
b) Vì M là trung điểm của AB nên ta có MA = MB = = 4 (cm).
Vì OM là đường trung trực của đoạn thẳng AB nên OM ⊥ AB hay ∆OAM vuông tại M.
Theo định lí Pythagore ta có: OA2 = OM2 + AM2
Suy ra OM2 = OA2 – AM2 = 52 – 42 = 9.
Do đó OM = 3 cm.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 93 Toán 9 Tập 1:
Mỗi bánh xe đạp ở Hình 1 gợi nên hình ảnh của một đường tròn.

Hai đường tròn đó có điểm chung hay không?
Hoạt động 1 trang 93 Toán 9 Tập 1:
Đồng hồ được mô tả ở Hình 2 có kim phút dài 12 cm. Khi kim phút quay một vòng thì đầu mút của kim phút vạch nên đường gì?

Luyện tập 1 trang 94 Toán 9 Tập 1:
Hãy chỉ ra một số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn.
Hoạt động 2 trang 94 Toán 9 Tập 1:
Quan sát Hình 5.

a) So sánh MN và OM + ON.
b) So sánh MN và AB.
Luyện tập 2 trang 95 Toán 9 Tập 1:
Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh MN < BC.
Hoạt động 3 trang 95 Toán 9 Tập 1:
Cho đường tròn (O; R).
a) Vẽ đường thẳng d đi qua tâm O cắt đường tròn tại A, B. So sánh OA và OB (Hình 7).
b) Giả sử M là một điểm tùy ý trên đường tròn (O; R). Trên tia đối của tia OM, ta lấy điểm N sao cho ON = OM. Điểm N có thuộc đường tròn (O; R) hay không?

Hoạt động 4 trang 95 Toán 9 Tập 1:
Cho đường tròn (O; R). Giả sử d là đường thẳng đi qua tâm O, M là một điểm tùy ý trên đường tròn (O; R). Kẻ MH vuông góc với d tại H. Trên tia MH lấy điểm N sao cho H là trung điểm của MN (ta gọi điểm N là điểm đối xứng với điểm M qua đường thẳng d). Điểm N có thuộc đường tròn (O; R) hay không?
Luyện tập 3 trang 96 Toán 9 Tập 1:
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm của hình đó.
Hoạt động 5 trang 96 Toán 9 Tập 1:
Bạn Đan vẽ năm vòng tròn minh họa cho biểu tượng của Thế vận hội Olympic như ở Hình 10. Hình vẽ đó thể hiện những cặp đường tròn cắt nhau. Theo em, hai đường tròn cắt nhau thì chúng có bao nhiêu điểm chung?

Hoạt động 6 trang 97 Toán 9 Tập 1:
Hình 12 mô tả các ống tròn xếp lên nhau và gợi nên hình ảnh các cặp đường tròn tiếp xúc nhau. Theo em, hai đường tròn tiếp xúc nhau thì chúng có bao nhiêu điểm chung?

Luyện tập 5 trang 98 Toán 9 Tập 1:
Cho hai đường tròn (O; 2,5 cm) và (O’; 4,5 cm). Tìm độ dài đoạn thẳng OO’, biết hai đường tròn đó tiếp xúc trong.
Hoạt động 7 trang 98 Toán 9 Tập 1:
Hình 14 mô tả hai bánh xe rời nhau, gợi nên hình ảnh hai đường tròn không giao nhau. Theo em, hai đường tròn không giao nhau thì có bao nhiêu điểm chung?

Luyện tập 4 trang 97 Toán 9 Tập 1:
Cho hai đường tròn (O; 14 cm), (O’; 5 cm) với OO’ = 8 cm. Hỏi hai đường tròn đó có cắt nhau hay không?
Bài 1 trang 99 Toán 9 Tập 1:
Trong Hình 16, có ba đường tròn với các đường kính lần lượt là AB, AC, CD. Hãy sắp xếp độ dài ba đoạn thẳng AB, AC, CD theo thứ tự tăng dần và giải thích kết quả tìm được
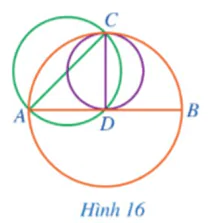
Bài 2 trang 100 Toán 9 Tập 1:
Xác định vị trí tương đối của hai đường tròn (O) và (O’) trong mỗi hình 17a, 17b, 17c, 17d:

Bài 3 trang 100 Toán 9 Tập 1:
Cho đoạn thẳng MN và đường thẳng a là đường trung trực của đoạn thẳng MN. Điểm O thuộc đường thẳng a.
a) Vẽ đường tròn tâm O bán kính R = OM.
b) Chứng minh điểm N thuộc đường tròn (O; R).
Bài 4 trang 100 Toán 9 Tập 1:
Cho đường tròn (O; R) và dây AB = R. Tính số đo góc AOB.
Bài 5 trang 100 Toán 9 Tập 1:
Chiếc đồng hồ trang trí ở Hình 18 gợi nên vị trí tương đối của các đường tròn.

Quan sát Hình 18 và chỉ ra một cặp đường tròn:
a) Cắt nhau;
b) Tiếp xúc ngoài;
c) Tiếp xúc trong;
d) Không giao nhau.
Bài 7 trang 100 Toán 9 Tập 1:
Cho hai đường tròn cùng tâm (O; R), (O; r) với R > r. Các điểm A, B thuộc đường tròn (O; R), các điểm A’ B’ thuộc đường tròn (O; r) sao cho O, A, A’ thẳng hàng; O, B, B’ thẳng hàng và điểm O không thuộc đường thẳng AB. Chứng minh:
a)
b) AB // A’B’.