Giải bài tập Bài 5 trang 79 Toán 9 Tập 2 | Toán 9 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 5 trang 79 Toán 9 Tập 2. Bài tập cuối chương 8. Toán 9 - Cánh diều
Đề bài:
Bài 5 trang 79 Toán 9 Tập 2: Cho tứ giác ABCD và các điểm M, N lần lượt thuộc các đoạn thẳng AB và CD sao cho các tứ giác AMND, BMNC là các tứ giác nội tiếp. Chứng minh 
Đáp án và cách giải chi tiết:
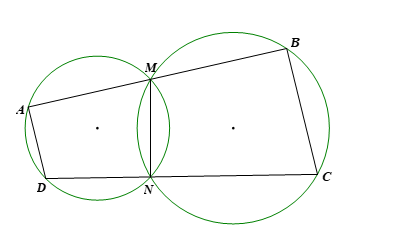
Tứ giác AMND là tứ giác nội tiếp nên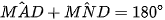 
(tổng hai góc đối nhau của tứ giác nội tiếp bằng 180°).
Tứ giác BMNC là tứ giác nội tiếp nên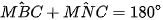 
(tổng hai góc đối nhau của tứ giác nội tiếp bằng 180°).
Suy ra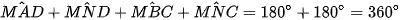 
.
Lại có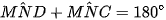 
(hai góc kề bù)
Nên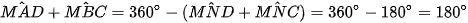 
Vậy
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 79 Toán 9 Tập 2
Bài 1 trang 79 Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn có 
Số đo góc A là:
A. 80°.
B. 160°.
C. 40°.
D. 100°.
Bài 2 trang 79 Toán 9 Tập 2
Bài 2 trang 79 Toán 9 Tập 2: Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh: 
Bài 3 trang 79 Toán 9 Tập 2
Bài 3 trang 79 Toán 9 Tập 2: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các đường cao AK, BM cắt nhau tại trực tâm H của tam giác ABC. Tia AK cắt đường tròn (O) tại điểm N (khác A). Chứng minh:
a) 
;
b) Tam giác BHN cân;
c) BC là đường trung trực của HN.
Bài 4 trang 79 Toán 9 Tập 2
Bài 4 trang 79 Toán 9 Tập 2: Cho tứ giác nội tiếp ABCD có hai tia CD và BA cắt nhau tại I. Chứng minh:
a)
b) 
Bài 6 trang 79 Toán 9 Tập 2
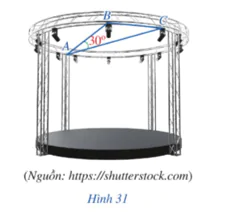
Bài 6 trang 79 Toán 9 Tập 2: Khung thép của một phần sân khấu có dạng đường tròn bán kính 15 m. Mắt của một người thợ ở vị trí A nhìn hai đèn ở các vị trí B, C (A, B, C cùng thuộc đường tròn bán kính 15 m), bằng cách nào đó, người thợ thấy rằng góc nhìn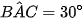 
(Hình 31). Khoảng cách giữa hai vị trí B, C bằng bao nhiêu mét?
