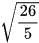Giải bài tập Bài 5 trang 34 Toán 9 Tập 1: | Toán 9 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 5 trang 34 Toán 9 Tập 1: . Bài 1. Bất đẳng thức.. Toán 9 - Cánh diều
Đề bài:
Nồng độ cồn trong máu (tiếng Anh là Blood Alcohol Content, viết tắt: BAC) được định nghĩa là tỉ lệ phần trăm lượng rượu (ethyl alcohol hoặc ethanol) trong máu của một người. Chẳng hạn, nồng độ cồn trong máu là 0,05% nghĩa là có 50 mg rượu trong 100 ml máu. Càng uống nhiều rượu bia thì nồng độ cồn trong máu càng cao và càng nguy hiểm khi tham gia giao thông. Nghị định 100/2019/NĐ-CP quy định mức xử phạt vi phạm hành chính đối với người điểu khiển xe gắn máy uống rượu bia khi tham gia giao thông như sau:
|
Mức độ vi phạm |
Hình thức xử phạt |
|
Mức 1: Nồng độ cồn trong máu dương và chưa vượt quá 50 mg/100 ml máu |
Từ 2 triệu đồng đến 3 triệu đồng và tước bằng lái xe từ 10 tháng đến 12 tháng |
|
Mức 2: Nồng độ cồn trong máu vượt quá 50 mg/100 ml máu và chưa vượt quá 80 mg/100 ml máu |
Từ 4 triệu đồng đến 5 triệu đồng và tước bằng lái xe từ 16 tháng đến 18 tháng |
|
Mức 3: Nồng độ cồn trong máu vượt quá 80 mg / 100 ml máu |
Từ 6 triệu đồng đến 8 triệu đồng và tước bằng lái xe từ 22 tháng đến 24 tháng |
Giả sử nồng độ cồn trong máu của một người sau khi uống rượu bia được tính theo công thức sau: y = 0,076 – 0,008t, trong đó y được tính theo đơn vị % và t là số giờ tính từ thời điểm uống rượu bia. Hỏi 3 giờ sau khi uống rượu bia, nếu người này điều khiển xe gắn máy tham gia giao thông thì sẽ bị xử phạt ở mức nào?

Đáp án và cách giải chi tiết:
Sau 3 giờ uống rượu bia, nồng độ cồn trong máu của người đó là:
y = 0,076 – 0,008.3 = 0,052 (%)
Tức là, nồng độ cồn trong máu là 52 mg rượu trong 100ml máu.
Do 50 < 52 < 80 nên nếu người này điều khiển xe gắn máy tham gia giao thông thì sẽ bị xử phạt ở mức 2, với hình thức xử phạt từ 4 triệu đồng đến 5 triệu đồng và tước bằng lái xe từ 16 tháng đến 18 tháng.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Khởi động trang 28 Toán 9 Tập 1:
Tìm hiểu trên Internet, bạn Minh được biết một con voi trưởng thành nặng khoảng 5 000 kg, một con hổ trưởng thành nặng khoảng 200 kg, một con tê giác đen trưởng thành nặng khoảng 450 kg.

Để biểu thị cân nặng của con voi hơn tổng cân nặng của cả con hổ và con tê giác đen, bạn Minh đã viết:
5 000 > 200 + 450.
Hệ thức dạng 5 000 > 200 + 450 gợi nên khái niệm gì trong toán học?
Hoạt động 1 trang 29 Toán 9 Tập 1:
Viết hệ thức thể hiện số thực a lớn hơn số thực b.
Luyện tập 2 trang 30 Toán 9 Tập 1:
Hãy viết hai cặp bất đẳng thức cùng chiều và hai cặp bất đẳng thức ngược chiều.
Hoạt động 2 trang 30 Toán 9 Tập 1:
Cho bất đẳng thức 15 > 14. Hãy so sánh hiệu 15 – 14 và 0.
Luyện tập 3 trang 30 Toán 9 Tập 1:
Cho a ≥ 2b. Chứng minh:
a) 2a – 1 ≥ a + 2b – 1;
b) 4b + 4a ≤ 5a + 2b.
Hoạt động 3 trang 30 Toán 9 Tập 1:
Cho bất đẳng thức a > b và cho số thực c.
a) Xác định dấu của hiệu: (a + c) – (b + c).
b) Hãy so sánh: a + c và b + c.
Luyện tập 4 trang 31 Toán 9 Tập 1:
Chứng minh:
a)
b) (a – 1)2 ≥ 4 – 2a với a2 ≥ 3.
Hoạt động 4 trang 31 Toán 9 Tập 1:
Cho bất đẳng thức a > b và số thực c > 0.
a) Xác định dấu của hiệu: ac – bc.
b) Hãy so sánh: ac và bc.
Hoạt động 5 trang 32 Toán 9 Tập 1:
Cho bất đẳng thức a > b và số thực c < 0.
a) Xác định dấu của hiệu: ac – bc.
b) Hãy so sánh: ac và bc.
Hoạt động 6 trang 32 Toán 9 Tập 1:
Cho các bất đẳng thức a > b và b > c.
a) Xác định dấu của các hiệu: a – b, b – c, a – c.
b) Hãy so sánh: a và c.
Luyện tập 7 trang 32 Toán 9 Tập 1:
Cho a, b, c, d là các số thực dương thỏa mãn a > b và c > d. Chứng minh: ac > bd.
Bài 1 trang 33 Toán 9 Tập 1:
Chứng minh:
a)
b) 26,2 < 2a + 3,2 < 26,4 với 11,5 < a < 11,6.
Bài 2 trang 34 Toán 9 Tập 1:
Chứng minh:
a) 2m + 4 > 2n + 3 với m > n;
b) –3a + 5 > –3b + 5 với a < b.
Bài 3 trang 34 Toán 9 Tập 1:
a) Cho a > b > 0. Chứng minh:
b) Áp dụng kết quả trên, hãy so sánh: và .
Bài 4 trang 34 Toán 9 Tập 1:
Chứng minh: x2 + y2 ≥ 2xy với hai số thực x, y tuỳ ý.