Giải bài tập Hoạt động 1 trang 48 Toán 11 Tập 2 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động 1 trang 48 Toán 11 Tập 2. Bài 4: Phương trình, bất phương trình mũ và lôgarit. Toán 11 - Cánh diều
Đề bài:
Trong bài toán ở phần mở đầu, giả sử r = 1,14%/năm.
a) Viết phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của luỹ thừa?
Đáp án và cách giải chi tiết:
a) Ta có công thức S = A . ert, trong đó:
⦁ A là dân số của năm lấy làm mốc tính;
⦁ S là dân số sau t năm;
⦁ r là tỉ lệ tăng dân số hằng năm, và r = 1,14%.
Để dân số sau t năm gấp đôi dân số ban đầu thì S = 2A
Suy ra 2A = A . e1,14%t nên e0,0114t = 2.
Vậy phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu là e0,0114t = 2.
b) Phương trình vừa tìm được có ẩn là t nằm ở số mũ của lũy thừa.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 54 Toán 11 Tập 2
Giải mỗi phương trình sau:
a) (0,3)x–3 = 1; b) 53x–2 = 25;
c) 9x–2 = 243x+1; d) ;
e) log5(3x – 5) = log5(2x + 1); g) .
Bài 2 trang 55 Toán 11 Tập 2
Giải mỗi bất phương trình sau:
a)
b)
c) 4x+3 ≥ 32x
d) log(x – 1) < 0
e)
g)ln(x + 3) ≥ ln(2x – 8)
Bài 4 trang 55 Toán 11 Tập 2
Sử dụng công thức tính mức cường độ âm L ở Ví dụ 14, hãy tính mức cường độ âm mà tai người có thể chịu đựng được, biết rằng giá trị cực đại của mức cường độ âm mà tai người có thể chịu đựng được là 130dB.
Câu hỏi khởi động trang 48 Toán 11 Tập 2
Dân số được ước tính theo công thức S = A . ert, trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau t năm, r là tỉ lệ tăng dân số hằng năm.
Hỏi sau bao nhiêu năm, dân số sẽ gấp đôi dân số của năm lấy làm mốc tính?
Hoạt động 2 trang 48 Toán 11 Tập 2
a) Vẽ đồ thị hàm số y = 3x và đường thẳng y = 7.
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình 3x = 7.
Luyện tập 2 trang 49 Toán 11 Tập 2
Giải mỗi phương trình sau:
a) 916 – x = 27x + 4; b) 16x – 2 = 0,25 . 2–x + 4.
Hoạt động 3 trang 49 Toán 11 Tập 2
Chỉ số thay đổi pH của một dung dịch được tính theo công thức: pH = – log[H+] (trong đó [H+] chỉ nồng độ ion hydrogen). Đo chỉ số pH của một số mẫu nước sông, ta có kết quả là pH = 6,1.
a) Viết phương trình thể hiện nồng độ x của hydrogen [H+] trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
Hoạt động 4 trang 50 Toán 11 Tập 2
a) Vẽ đồ thị hàm số y = log4x và đường thẳng y = 5.
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình log4x = 5.
Luyện tập 4 trang 51 Toán 11 Tập 2
Giải mỗi phương trình sau:
a) log5(2x - 4) + (x - 1) = 0;
b) log2x + log4x = 3.
Hoạt động 5 trang 51 Toán 11 Tập 2
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số y = . Từ đó, hãy tìm x sao cho > 2.

Luyện tập 5 trang 52 Toán 11 Tập 2
Cho hai ví dụ về bất phương trình mũ cơ bản.
Luyện tập 6 trang 52 Toán 11 Tập 2
Giải mỗi bất phương trình sau:
a) 7x+3 < 343; b) ≥ 3.
Hoạt động 6 trang 53 Toán 11 Tập 2
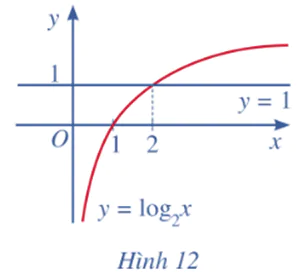
Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit y = log2x. Từ đó, hãy tìm x sao cho log2x > 1.
Luyện tập 7 trang 53 Toán 11 Tập 2
Cho hai ví dụ về bất phương trình logarit cơ bản.
Luyện tập 8 trang 54 Toán 11 Tập 2
Giải mỗi bất phương trình sau:
a) log3x < 2; b) (x - 5) ≥ -2.
Bài 3 trang 55 Toán 11 Tập 2
Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất x%/năm (x > 0). Sau 3 năm, người đó rút được cả gốc và lãi là 119,1016 triệu đồng. Tìm x, biết rằng lãi suất không thay đổi qua các năm và người đó không rút tiền ra trong suốt quá trình gửi.