Giải bài tập HĐ8 trang 92 Toán 11 Tập 2 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập HĐ8 trang 92 Toán 11 Tập 2. Bài 32: Các quy tắc tính đạo hàm. Toán 11 - Kết nối tri thức
Đề bài:
Giới hạn cơ bản của hàm số mũ và hàm số lôgarit
a) Sử dụng phép đổi biến t = , tìm giới hạn .
b) Với y = , tính ln y và tìm giới hạn của .
c) Đặt t = ex – 1. Tính x theo t và tìm giới hạn .
Đáp án và cách giải chi tiết:
a)
Ta có: t = , nên khi x → 0 thì t → + ∞ do đó:
.
b) Với y = , ta có:
ln y = ln = .
Khi đó, .
c)
t = ex – 1 ⇔ ex = t + 1 ⇔ x = ln(t + 1).
Ta có: .
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 9.12 trang 94 Toán 11 Tập 2
Chuyển động của một hạt trên một dây rung được cho bởi s(t) = 12 + 0,5sin(4πt), trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu?
Mở đầu trang 88 Toán 11 Tập 2
Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu v0 = 20 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí, độ cao h so với mặt đất (tính bằng mét) của vật tại thời điểm t (giây) sau khi ném được cho bởi công thức sau:
h = vot - gt2,
trong đó, v0 là vận tốc ban đầu của vật, g = 9,8 m/s2 là gia tốc rơi tự do. Hãy tính vận tốc của vật khi nó đạt độ cao cực đại và khi nó chạm đất.
HĐ4 trang 90 Toán 11 Tập 2
Nhận biết quy tắc đạo hàm của hàm số hợp
Cho các hàm số y = u2 và u = x2 + 1.
a) Viết công thức của hàm số hợp y = (u(x))2 theo biến x.
b) Tính và so sánh: y'(x) và y' (u) . u' (x).
HĐ5 trang 91 Toán 11 Tập 2
Xây dựng công thức tính đạo hàm của hàm số y = sin x
a) Với h ≠ 0, biến đổi hiệu sin(x + h) – sin x thành tích.
b) Sử dụng đẳng thức giới hạn và kết quả của câu a, tính đạo hàm của hàm số y = sin x tại điểm x bằng định nghĩa.
HĐ6 trang 91 Toán 11 Tập 2
Xây dựng công thức tính đạo hàm của hàm số y = cos x
Bằng cách viết y = cos x = sin, tính đạo hàm của hàm số y = cos x.
HĐ7 trang 92 Toán 11 Tập 2
Xây dựng công thức tính đạo hàm của các hàm số y = tan x và y = cot x
a) Bằng cách viết y = tan x = , tính đạo hàm của hàm số y = tan x.
b) Sử dụng hằng đẳng thức cot x = tan với x ≠ kπ (), tính đạo hàm của hàm số y = cot x.
Vận dụng 1 trang 92 Toán 11 Tập 2
Một vật chuyển động có phương trình s(t) = 4cos(2πt - ) (m), với t là thời gian tính bằng giây. Tính vận tốc của vật khi t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).
HĐ9 trang 93 Toán 11 Tập 2
Xây dựng công thức tính đạo hàm của hàm số mũ
a) Sử dụng giới hạn và đẳng thức ex + h – ex = ex(eh – 1), tính đạo hàm của hàm số y = ex tại x bằng định nghĩa.
b) Sử dụng hằng đẳng thức ax = exlna (0 < a ≠ 1), hãy tính đạo hàm của hàm số y = ax.
Luyện tập 6 trang 93 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau:
a) y = ;
b) y = 3sin x .
HĐ10 trang 93 Toán 11 Tập 2
Xây dựng công thức tính đạo hàm của hàm số lôgarit
a) Sử dụng giới hạn và đẳng thức ln(x + h) – lnx = , tính đạo hàm của hàm số y = ln x tại điểm x > 0 bằng định nghĩa.
b) Sử dụng đẳng thức (0 < a ≠ 1), hãy tính đạo hàm của hàm số y = logax.
Vận dụng 2 trang 94 Toán 11 Tập 2
Ta đã biết, độ pH của một dung dịch được xác định bởi pH = –log[H+], ở đó [H+] là nồng độ (mol/lít) của ion hydrogen. Tính tốc độ thay đổi của pH đối với nồng độ [H+].
Bài 9.6 trang 94 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau:
a) y = x3 – 3x2 + 2x + 1;
b) 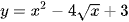 .
.
Bài 9.8 trang 94 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau:
a) y = xsin2x;
b) y = cos2x + sin2x;
c) y = sin3x – 3sinx;
d) y = tanx + cotx.
Bài 9.9 trang 94 Toán 11 Tập 2
Tính đạo hàm các hàm số sau:
a) ![]() ;
;
b) y = log3(4x + 1).
Bài 9.10 trang 94 Toán 11 Tập 2
Cho hàm số 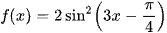 . Chứng minh rằng |f'(x)| ≤ 6 với mọi x.
. Chứng minh rằng |f'(x)| ≤ 6 với mọi x.
Bài 9.11 trang 94 Toán 11 Tập 2
Một vật chuyển động rơi tự do có phương trình h(t) = 100 – 4,9t2, ở đó độ cao h so với mặt đất tính bằng mét và thời gian t tính bằng giây. Tính vận tốc của vật:
a) Tại thời điểm t = 5 giây;
b) Khi vật chạm đất.