Giải bài tập HĐ2 trang 96 Toán 11 Tập 2 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập HĐ2 trang 96 Toán 11 Tập 2. Bài 33: Đạo hàm cấp hai. Toán 11 - Kết nối tri thức
Đề bài:
Nhận biết ý nghĩa cơ học của đạo hàm cấp hai
Xét một chuyển động có phương trình s = 4cos(2πt).
a) Tính vận tốc tức thời của chuyển động tại thời điểm t.
b) Tính gia tốc tức thời tại thời điểm t.
Đáp án và cách giải chi tiết:
a) Ta có: v(t) = s'(t) = –4.2πsin(2πt) = –8πsin(2πt).
Vậy vận tốc tức thời của chuyển động tại thời điểm t là –8πsin(2πt).
b) Gia tốc tức thời tại thời điểm t là
a(t) = v'(t) = [–8πsin(2πt)]' = –8π.2πcos(2πt) = –16π2cos(2πt).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 9.16 trang 96 Toán 11 Tập 2
Cho hàm số . Chứng minh rằng |f''(x)| ≤ 4 với mọi x.
Bài 9.15 trang 96 Toán 11 Tập 2
Cho hàm số P(x) = ax2 + bx + 3 (a, b là hằng số). Tìm a, b biết P'(1) = 0 và P''(1) = –2.
Bài 9.14 trang 96 Toán 11 Tập 2
Tính đạo hàm cấp hai của các hàm số sau:
a) y = ln(x + 1);
b) y = tan2x.
Mở đầu trang 95 Toán 11 Tập 2
Chuyển động của một vật gắn trên con lắc lò xo (khi bỏ qua ma sát và sức cản không khí) được cho bởi phương trình sau:
x(t) = 4cos(2πt + );
ở đó x tính bằng centimet và thời gian t tính bằng giây. Tìm gia tốc tức thời của vật tại thời điểm t = 5 giây (làm tròn kết quả đến hàng đơn vị).
HĐ1 trang 95 Toán 11 Tập 2
Nhận biết đạo hàm cấp hai của một hàm số
a) Gọi g(x) là đạo hàm của hàm số y = sin(2x + ). Tìm g(x).
b) Tính đạo hàm của hàm số y = g(x).
Luyện tập 1 trang 95 Toán 11 Tập 2
Tính đạo hàm cấp hai của các hàm số sau:
a) y = xe2x;
b) y = ln(2x + 3).
Vận dụng trang 96 Toán 11 Tập 2
Một chuyển động thẳng có phương trình s = 2t2 + t4 (s tính bằng mét, t tính bằng giây). Tìm gia tốc của vật tại thời điểm t = 4 giây.
Bài 9.17 trang 96 Toán 11 Tập 2
Phương trình chuyển động của một hạt được cho bởi 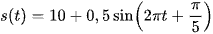 , trong đó s tính bằng centimet và t tính bằng giây. Tính gia tốc của hạt tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).
, trong đó s tính bằng centimet và t tính bằng giây. Tính gia tốc của hạt tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).